Fluorescence¶
Theory and adaptation into freeART¶
The fluorescence projector is caracterized by the fact that the detector is not receiving directly the beam from the X ray source (incoming beam - Red) but an other beam (outgoing beam - Orange) which is generated from an interaction between the sample and the incoming beam. As the outgoing beam is produced with a random direction, the detector will only receive a fraction of all beams produced. This effect is taking incto account in FreeARt (aka solidAngle). You can see the scheme bellow which model the process.
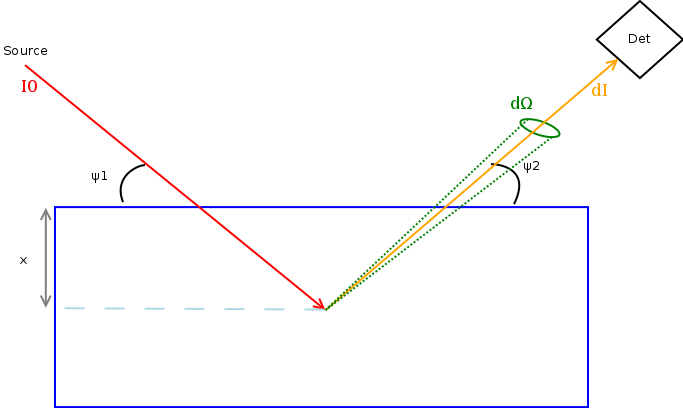
Those two beam can have the same energy. In this case we are in the COMPTON mode.
If they have different energies then we are in the FLUORESENCE mode.
In fact on an algorithmic point of view this doesn t change a lot the calculation. The only difference is that for COMPTON you will give the same absorption matrix for the incominc beam (absMat) and the outgoing beam (selfAbsMat).
The formula giving the emission rate of the element i detected is (for one ray) :
with :
- \(e^{-\frac{{\mu}_{E_0}{\rho}x}{sin({\psi}_1)}}\) : Rate of incident photons at depth x (1) and \({\mu}_{E_0}{\rho}x\) is the absorption of the incoming beam
- \(\frac{{\rho}C_i{\tau}_{is} (E_0)}{sin({\psi_1})}dx\) : Probability of production of vacancy in the atomic shell s of the element i in the path \(\frac{dx}{sin{\psi}_1}\) (2)
- \({\omega}_{is} R_{is} (E_F)\) : Probability of emission of a photon of energy \(E_F\) of the element i among the family of emitted photons corresponding to transitions to the atomic shell (3)
- \(e^{-\frac{{\mu}_{E_F}{\rho}x}{sin({\psi}_2)}}\) : Transmission of the fluorescent radiation in the outgoing path towards the detector (4) and \({\mu}_{E_F}\) is the absorption of the outgoing beam
- \(\frac{d{\Omega}}{4{\pi}}{\epsilon}_D(E_F, {\Omega})\) : overall detection efficiency for \(E_F\) photons (aka solid angle) (5)
In FreeART for now \(I_0=1\) Then the geometry (distane that each beam is going trought, solid angle, ...) is deduced. What you should give to FreeART is :
- \({\mu}_{E_0}{\rho}\) from the “absorption” matrix
- \({\mu}_{E_F}{\rho}\) from the “self absorption” matrix
- probabilty of production of a photon of energy \(E_F\) of the element i for each voxel (including the probability of production of a vacancy in the atomic shell s of the element i) from the “phantom” matrix
Detector(s)¶
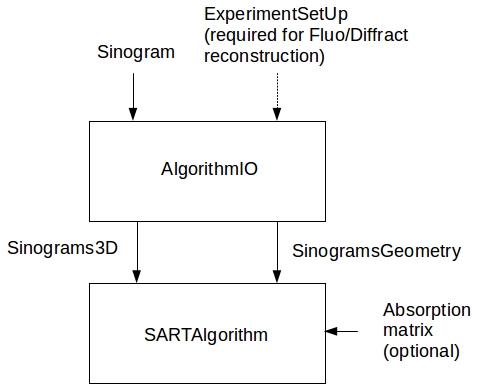
To use FreeART for fluorescence reconstruction, FreeART requires informations about the added fluorescence detector(s) in order to compute the Solid angle specially. To pass them to FreeART, you need to create one instance of the FreeART ExperimentSetUp class. This ExperimentSetUp class is nothing more than a C++ vector of DetectorSetUp class instances. For each fluorescence detector(s) in the geometry, you create one instance of this DetectorSetUp class from:
- The position of detector point C for the first incoming beam angle defined in the sinogram
- The width of the detector (distance DC)
Then, with the sinogram file and using the FreeART AlgorithmIO class, you are able to generate the two inputs of the FreeART SARTAlgorithm class. This is explained by the following drawing.
Sinogram¶
Obviously freeART will also need a sinogram obtain fron a fluorescence detector
Absorption matrice(s)¶
We have to set to the ARTAlgorithm the absorption for each voxel of the incoming beam and of the outgoing beam. wich are respectively \({\mu}_{E_0}\) and \({\mu}_{E_F}\) in the formula presented in “Theory and adaptation into freeART”. Those absorptions are normalized and set in \(g.cm^{-2}\).
- For compton (case \({E_0}\) == \({E_F}\)) the absorption matrix (matrix defining for each voxel the absorption of the incoming beam) is the same as the self absorption matrix (matrix defining for each voxel the absorption of the outgoing beam)
- For fluorescence (case \({E_0}\) != \({E_F}\)) the absorption matrix and the self absorption matrix are different.
But the algorithm used is the same.
Options to compute beam’s ray value¶
We have two ways to compute the values of the beams in the rays :
- with interpolation we will interpolate the value of the beam from the 4 neighboring voxels values and the distance to their center
- without interpolation we will take the value of the voxel the beam is in and only this value (reduce memory cost by four)
you can set those values :
- from cpp
rp.setRayPointCalculationMethod(RayPointCalculationMethod::withInterpolation)
- from python
al.setRayPointCalculationMethod(raypointsmethod.withInterpolation)
Options to compute outgoing rays¶
We have three methods to compute the outgoing rays.
- rawApproximation : in this case we are making the evaluation of the outgoing ray the faster as possible by computing for each rotation the mean value of some outgoing rays and taking it as the value of the voxel
- createOneRayPerSamplePoint : in this version we are creating the real outgoing ray for each sample point on the incoming ray and computing the ‘real’ outgoing absorption of the ray by sampling voxels
- matriceSubdivision : this is the raw approximation case but by subdividing the voxels for the outgoing rays we are reducing the noise of the “raw” approximation.
Setting outgoing ray algorithm :
- from cpp
rp.setOutgoingRayAlgorithm(OutgoingRayAlgorithm::rawApproximation)
- from python
al.setOutgoingRayAlgorithm(outgoingrayalgorithm.rawApproximation)
Example of forward projection¶
From python¶
# define reconstruction parameters
al = freeart.FluoFwdProjection(
phMatr = phantom,
expSetUp = detSetup,
absorpMatr = absMat,
selfAbsorpMatrix = selfAbsMat,
angleList = None,
minAngle = 0,
maxAngle = 2.0*np.pi,
anglesNb = numAngle )
al.setOverSampling(oversampling)
al.setSamplingWithInterpolation(samplingWithInterpolation)
al.setCreateOneRayPerSamplePt(createOneRayPerSamplePoint)
# create the sinogram
sinogram, angles = al.makeSinogram()
Note
you can see a more detaillled example in the freeart/python_utils/example_fluo.py file
From cpp¶
// set up geometry and absorption matrices from a phantom file
algoIO.prepareSinogramGeneration(phantomFileName, esu, 0.0, 2.0*M_PI, 125, phantom, sinosGeo);
// load the matrix of absorption of the incoming rays
algoIO.loadAbsorptionMatrix(absorpMatrixFileName, absorpMatrix);
// load the matrix of absorption of the outgoing rays
algoIO.loadAbsorptionMatrix(selfAbsorpMatrixFileName, selfAbsorpMatrix);
// build the SART algorithm
FreeART::SARTAlgorithm<double,FreeART::FluoReconstruction> *al = NULL;
al = new FreeART::SARTAlgorithm<double,FreeART::FluoReconstruction>(phantom, absorpMatrix, selfAbsorpMatrix, sinosGeo);
// launch the projection
al->makeSinogram();
// get the sinogram generated
GenericSinogram3D<double> sinogram = al->getSinogram();
Note
you can see a example of a fluorescence projection done in cpp using FreeART in the file : /freeart/cpp_utils/projector_fluo.cpp
Example of reconstruction¶
If we already have the absorption matrices (incoming and outgoing) you can run your reconstruction
From python¶
alRecons = freeart.FluoBckProjection(sinoDat=_sinogram, sinoAngles=_angles, expSetUp=_detSetup, absorp=_absMat, selfAbsorp=_selfAbsMat)
alRecons.setOverSampling(10)
alRecons.setDampingFactor(0.2)
alRecons.setCreateOneRayPerSamplePt(True)
From cpp¶
// set up the geometry (sinosGeo) and the stack of sinogram (sinos) from the sinogram file (sinoFile), the experiment setup (esu)
algoIO.buildSinogramGeometry(sinoFile, esu, sinos, sinosGeo);
//load abs ans selfAbs matrices
algoIO.loadAbsorptionMatrix(absorpFile, absorpMatr);
algoIO.loadAbsorptionMatrix(selfAbsorpFile, selfAbsorpMatr);
// create the fluorescence reconstruction
FreeART::SARTAlgorithm<double,FreeART::FluoReconstruction> *al;
al = new FreeART::SARTAlgorithm<double,FreeART::FluoReconstruction>(sinos, absorpMatr, selfAbsorpMatr, sinosGeo);
// Launch the reconstruction on itterNb iterations
al->doWork(iterNb)
const FreeART::BinVec3D<double>* v = &(al->getPhantom());
Note
you can see a complete example of the fluorescence reconstruction in the /freeart/cpp_utils/reconstr_fluo.cpp file
A Fluorescence Reconstruction¶
Generally when you want to run a fluorescence reconstruction you have to define the self absorption matrix that you can’t get from the manipulation.
In order to do so we have created some routines in python to obtain this self absorption matrices from \({E_0}\), a matrix defining the material we have for each voxle (wich can be created using tomoGUI) and the composition of each materials ( to obtain absorption at \({E_0}\) from fisx ).
Then you can use the freeart routine by using directly the configinterpreter.
An example is given in examples/python/absorptionEffect.py. The sample is a simple homogeneous square. In here a sinogram is created using an absorption matrix and a self absorption matrix. Then we run three differente reconstructions :
- one with a null absorption and self absorption
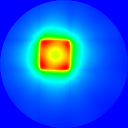
- one with the absorption of the incoming beam and no self absorption
- one with the two (absorption and self absorption)