Demo of usage of the MultiGeometry class of pyFAI

For this tutorial, we will use the ipython notebook, now known as Jypyter, an take advantage of the integration of matplotlib with the inline:

%pylab inline

Populating the interactive namespace from numpy and matplotlib

The multi_geometry module of pyFAI allows you to integrate multiple images taken at various image position, all togeather. This tutorial will explain you how to perform azimuthal integration in three use-case: translation of the detector, rotation of the detector around the sample and finally how to fill gaps of a pixel detector. But before, we need to know how to generate fake diffraction image.

Generation of diffraction images

PyFAI knows about 20 different reference sample called calibrants. We will use them to generate fake diffraction images knowing the detector and its position in space

import pyFAI
import pyFAI.calibrant
print("Number of known calibrants: %s"%len(pyFAI.calibrant.ALL_CALIBRANTS))
print(" ".join(pyFAI.calibrant.ALL_CALIBRANTS.keys()))

Number of known calibrants: 27
Ni CrOx NaCl Si_SRM640e Si_SRM640d Si_SRM640a Si_SRM640c alpha_Al2O3 Cr2O3 AgBh Si_SRM640 CuO PBBA Si_SRM640b quartz C14H30O cristobaltite Si LaB6 CeO2 LaB6_SRM660a LaB6_SRM660b LaB6_SRM660c TiO2 ZnO Al Au

wl = 1e-10
LaB6 = pyFAI.calibrant.ALL_CALIBRANTS("LaB6")
LaB6.set_wavelength(wl)
print(LaB6)

LaB6 Calibrant at wavelength 1e-10

We will start with a “simple” detector called Titan (build by Oxford Diffraction but now sold by Agilent). It is a CCD detector with scintilator and magnifying optics fibers. The pixel size is constant: 60µm

det = pyFAI.detectors.Titan()
print(det)
p1, p2, p3 = det.calc_cartesian_positions()
print("Detector is flat, P3= %s"%p3)
poni1 = p1.mean()
poni2 = p2.mean()
print("Center of the detector: poni1=%s poni2=%s"%(poni1, poni2))

Detector Titan 2k x 2k       PixelSize= 6.000e-05, 6.000e-05 m
Detector is flat, P3= None
Center of the detector: poni1=0.06144 poni2=0.06144

The detector is placed orthogonal to the beam at 10cm. This geometry is saved into an AzimuthalIntegrator instance:

ai = pyFAI.AzimuthalIntegrator(dist=0.1, poni1=poni1, poni2=poni2, detector=det)
ai.set_wavelength(wl)
print(ai)

Detector Titan 2k x 2k       PixelSize= 6.000e-05, 6.000e-05 m
Wavelength= 1.000000e-10m
SampleDetDist= 1.000000e-01m        PONI= 6.144000e-02, 6.144000e-02m       rot1=0.000000  rot2= 0.000000  rot3= 0.000000 rad
DirectBeamDist= 100.000mm   Center: x=1024.000, y=1024.000 pix      Tilt=0.000 deg  tiltPlanRotation= 0.000 deg

Knowing the calibrant, the wavelength, the detector and the geometry, one can simulate the 2D diffraction pattern:

img = LaB6.fake_calibration_image(ai)
imshow(img, origin="lower")

<matplotlib.image.AxesImage at 0x7fbf946e68d0>

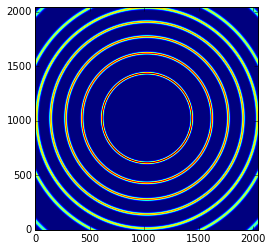
This image can be integrated in q-space and plotted:

plot(*ai.integrate1d(img, 1000, unit="q_A^-1"))

[<matplotlib.lines.Line2D at 0x7fbf92da9d90>]

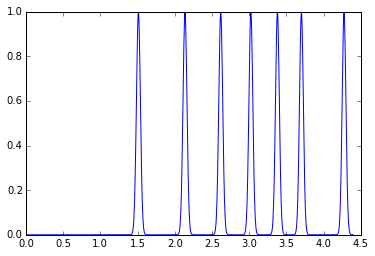
Note pyFAI does now about the ring position but nothing about relative intensities of rings.

Translation of the detector along the vertical axis

The vertical axis is defined along the poni1. If one moves the detector higher, the poni will appear at lower coordinates. So lets define 5 upwards verical translations of half the detector size.

For this we will duplicate 5x the AzimuthalIntegrator object, but instances of AzimuthalIntegrator are mutable, so it is important to create an actual copy and not an view on them. In Python, one can use the copy function of the copy module:

import copy

We will now offset the poni1 value of each AzimuthalIntegratoe which correspond to a vertical translation. Each subsequent image is offsetted by half a detector width (stored as poni1).

ais = []
imgs = []
fig, plots = subplots(1,5)
for i in range(5):
    my_ai = copy.deepcopy(ai)
    my_ai.poni1 -= i*poni1
    my_img = LaB6.fake_calibration_image(my_ai)
    plots[i].imshow(my_img, origin="lower")
    ais.append(my_ai)
    imgs.append(my_img)
    print(my_ai)

Detector Titan 2k x 2k       PixelSize= 6.000e-05, 6.000e-05 m
Wavelength= 1.000000e-10m
SampleDetDist= 1.000000e-01m        PONI= 6.144000e-02, 6.144000e-02m       rot1=0.000000  rot2= 0.000000  rot3= 0.000000 rad
DirectBeamDist= 100.000mm   Center: x=1024.000, y=1024.000 pix      Tilt=0.000 deg  tiltPlanRotation= 0.000 deg
Detector Titan 2k x 2k       PixelSize= 6.000e-05, 6.000e-05 m
Wavelength= 1.000000e-10m
SampleDetDist= 1.000000e-01m        PONI= 0.000000e+00, 6.144000e-02m       rot1=0.000000  rot2= 0.000000  rot3= 0.000000 rad
DirectBeamDist= 100.000mm   Center: x=1024.000, y=0.000 pix Tilt=0.000 deg  tiltPlanRotation= 0.000 deg
Detector Titan 2k x 2k       PixelSize= 6.000e-05, 6.000e-05 m
Wavelength= 1.000000e-10m
SampleDetDist= 1.000000e-01m        PONI= -6.144000e-02, 6.144000e-02m      rot1=0.000000  rot2= 0.000000  rot3= 0.000000 rad
DirectBeamDist= 100.000mm   Center: x=1024.000, y=-1024.000 pix     Tilt=0.000 deg  tiltPlanRotation= 0.000 deg
Detector Titan 2k x 2k       PixelSize= 6.000e-05, 6.000e-05 m
Wavelength= 1.000000e-10m
SampleDetDist= 1.000000e-01m        PONI= -1.228800e-01, 6.144000e-02m      rot1=0.000000  rot2= 0.000000  rot3= 0.000000 rad
DirectBeamDist= 100.000mm   Center: x=1024.000, y=-2048.000 pix     Tilt=0.000 deg  tiltPlanRotation= 0.000 deg
Detector Titan 2k x 2k       PixelSize= 6.000e-05, 6.000e-05 m
Wavelength= 1.000000e-10m
SampleDetDist= 1.000000e-01m        PONI= -1.843200e-01, 6.144000e-02m      rot1=0.000000  rot2= 0.000000  rot3= 0.000000 rad
DirectBeamDist= 100.000mm   Center: x=1024.000, y=-3072.000 pix     Tilt=0.000 deg  tiltPlanRotation= 0.000 deg

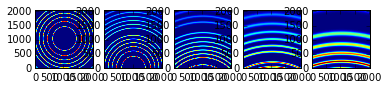
MultiGeometry integrator

The MultiGeometry instance can be created from any list of AzimuthalIntegrator instances or list of poni-files. Here we will use the former method.

The main difference of a MultiIntegrator with a “normal” AzimuthalIntegrator comes from the definition of the output space in the constructor of the object. One needs to specify the unit and the integration range.

from pyFAI.multi_geometry import MultiGeometry

mg = MultiGeometry(ais, unit="q_A^-1", radial_range=(0, 10))
print(mg)

MultiGeometry integrator with 5 geometries on (0, 10) radial range (q_A^-1) and (-180, 180) azimuthal range (deg)

MultiGeometry integrators can be used in a similar way to “normal” AzimuthalIntegrators. Keep in mind the output intensity is always scaled to absolute solid angle.

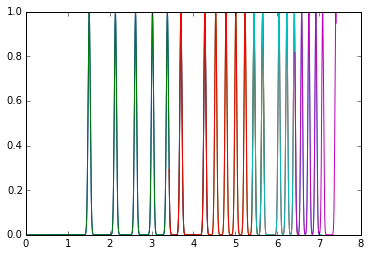
plot(*mg.integrate1d(imgs, 10000))

[<matplotlib.lines.Line2D at 0x7fbf90a4a210>]

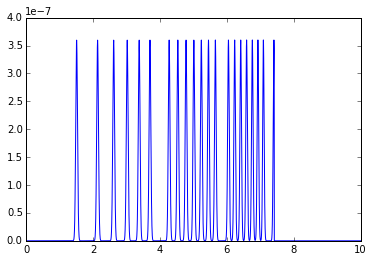
for i, a in zip(imgs, ais):
    plot(*a.integrate1d(i, 1000, unit="q_A^-1"))

Rotation of the detector

The strength of translating the detector is that it simulates a larger detector, but this approach reaches its limit quikly as the higher the detector gets, the smallest the solid angle gets and induces artificial noise. One solution is to keep the detector at the same distance and rotate the detector.

Creation of diffraction images

In this example we will use a Pilatus 200k with 2 modules. It has a gap in the middle of the two detectors and we will see how the MultiGeometry can help.

As previously, we will use LaB6 but instead of translating the images, we will rotate them along the second axis:

det = pyFAI.detectors.detector_factory("pilatus200k")
p1, p2, p3 = det.calc_cartesian_positions()
print(p3)
poni1 = p1.mean()
poni2 = p2.mean()
print(poni1)
print(poni2)

None
0.035002
0.041882

ai = pyFAI.AzimuthalIntegrator(dist=0.1, poni1=poni1, poni2=poni2, detector=det)
img = LaB6.fake_calibration_image(ai)
imshow(img, origin="lower")
#imshow(log(ai.integrate2d(img, 500, 360, unit="2th_deg")[0]))

<matplotlib.image.AxesImage at 0x7fbf90923790>

plot(*ai.integrate1d(img, 500,unit="2th_deg"))

[<matplotlib.lines.Line2D at 0x7fbf90847490>]

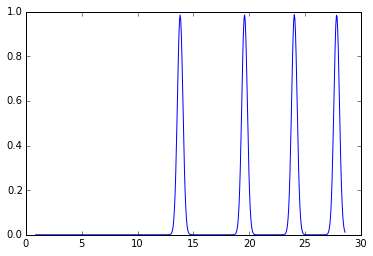
We will rotate the detector with a step size of 15 degrees

step = 15*pi/180
ais = []
imgs = []
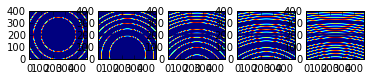
fig, plots = subplots(1,5)
for i in range(5):
    my_ai = copy.deepcopy(ai)
    my_ai.rot2 -= i*step
    my_img = LaB6.fake_calibration_image(my_ai)
    plots[i].imshow(my_img, origin="lower")
    ais.append(my_ai)
    imgs.append(my_img)
    print(my_ai)

Detector Pilatus200k         PixelSize= 1.720e-04, 1.720e-04 m
SampleDetDist= 1.000000e-01m        PONI= 3.500200e-02, 4.188200e-02m       rot1=0.000000  rot2= 0.000000  rot3= 0.000000 rad
DirectBeamDist= 100.000mm   Center: x=243.500, y=203.500 pix        Tilt=0.000 deg  tiltPlanRotation= 0.000 deg
Detector Pilatus200k         PixelSize= 1.720e-04, 1.720e-04 m
SampleDetDist= 1.000000e-01m        PONI= 3.500200e-02, 4.188200e-02m       rot1=0.000000  rot2= -0.261799  rot3= 0.000000 rad
DirectBeamDist= 103.528mm   Center: x=243.500, y=47.716 pix Tilt=15.000 deg  tiltPlanRotation= -90.000 deg
Detector Pilatus200k         PixelSize= 1.720e-04, 1.720e-04 m
SampleDetDist= 1.000000e-01m        PONI= 3.500200e-02, 4.188200e-02m       rot1=0.000000  rot2= -0.523599  rot3= 0.000000 rad
DirectBeamDist= 115.470mm   Center: x=243.500, y=-132.169 pix       Tilt=30.000 deg  tiltPlanRotation= -90.000 deg
Detector Pilatus200k         PixelSize= 1.720e-04, 1.720e-04 m
SampleDetDist= 1.000000e-01m        PONI= 3.500200e-02, 4.188200e-02m       rot1=0.000000  rot2= -0.785398  rot3= 0.000000 rad
DirectBeamDist= 141.421mm   Center: x=243.500, y=-377.895 pix       Tilt=45.000 deg  tiltPlanRotation= -90.000 deg
Detector Pilatus200k         PixelSize= 1.720e-04, 1.720e-04 m
SampleDetDist= 1.000000e-01m        PONI= 3.500200e-02, 4.188200e-02m       rot1=0.000000  rot2= -1.047198  rot3= 0.000000 rad
DirectBeamDist= 200.000mm   Center: x=243.500, y=-803.506 pix       Tilt=60.000 deg  tiltPlanRotation= -90.000 deg

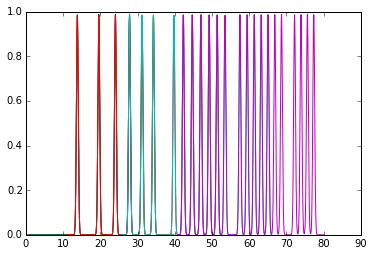
for i, a in zip(imgs, ais):
    plot(*a.integrate1d(i, 1000, unit="2th_deg"))

Creation of the MultiGeometry

This time we will work in 2theta angle using degrees:

mg = MultiGeometry(ais, unit="2th_deg", radial_range=(0, 90))
print(mg)
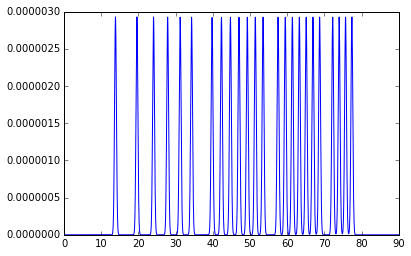
plot(*mg.integrate1d(imgs, 10000))

MultiGeometry integrator with 5 geometries on (0, 90) radial range (2th_deg) and (-180, 180) azimuthal range (deg)
area_pixel=1.32053624453 area_sum=2.69418873745, Error= -1.04022324159

[<matplotlib.lines.Line2D at 0x7fbf903e2650>]

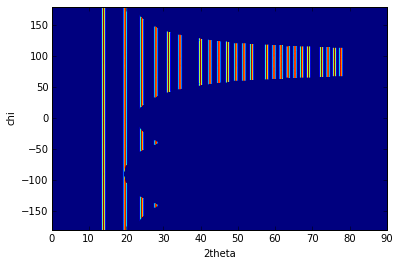
I,tth, chi = mg.integrate2d(imgs, 1000,360)
imshow(I, origin="lower",extent=[tth.min(), tth.max(), chi.min(), chi.max()], aspect="auto")
xlabel("2theta")
ylabel("chi")

<matplotlib.text.Text at 0x7fbf90330350>

How to fill-up gaps in arrays of pixel detectors during 2D integration

We will use ImXpad detectors which exhibits large gaps.

det = pyFAI.detectors.detector_factory("Xpad_flat")
p1, p2, p3 = det.calc_cartesian_positions()
print(p3)
poni1 = p1.mean()
poni2 = p2.mean()
print(poni1)
print(poni2)

None
0.076457
0.0377653

ai = pyFAI.AzimuthalIntegrator(dist=0.1, poni1=0, poni2=poni2, detector=det)
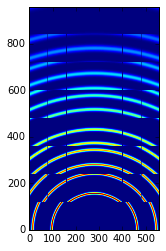
img = LaB6.fake_calibration_image(ai)
imshow(img, origin="lower")

<matplotlib.image.AxesImage at 0x7fbf909b8210>

I, tth, chi=ai.integrate2d(img, 500, 360, azimuth_range=(0,180), unit="2th_deg", dummy=-1)
imshow(sqrt(I),origin="lower",extent=[tth.min(), tth.max(), chi.min(), chi.max()], aspect="auto")
xlabel("2theta")
ylabel("chi")

-c:2: RuntimeWarning: invalid value encountered in sqrt

<matplotlib.text.Text at 0x7fbf90a67850>

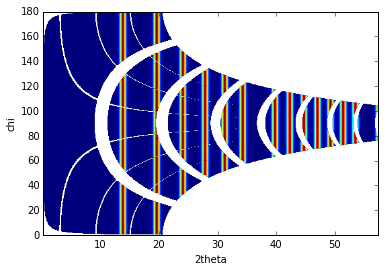
To observe textures, it is mandatory to fill the large empty space. This can be done by tilting the detector by a few degrees to higher 2theta angle (yaw 2x5deg) and turn the detector along the azimuthal angle (roll 2x5deg):

step = 5*pi/180
nb_geom = 3
ais = []
imgs = []
for i in range(nb_geom):
    for j in range(nb_geom):
        my_ai = copy.deepcopy(ai)
        my_ai.rot2 -= i*step
        my_ai.rot3 -= j*step
        my_img = LaB6.fake_calibration_image(my_ai)
        ais.append(my_ai)
        imgs.append(my_img)
mg = MultiGeometry(ais, unit="2th_deg", radial_range=(0, 60), azimuth_range=(0, 180), empty=-1)
print(mg)
I, tth, chi = mg.integrate2d(imgs, 1000, 360)
imshow(sqrt(I),origin="lower",extent=[tth.min(), tth.max(), chi.min(), chi.max()], aspect="auto")
xlabel("2theta")
ylabel("chi")

MultiGeometry integrator with 9 geometries on (0, 60) radial range (2th_deg) and (0, 180) azimuthal range (deg)

-c:16: RuntimeWarning: invalid value encountered in sqrt

<matplotlib.text.Text at 0x7fbf92c74710>

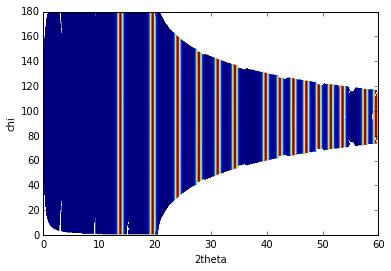
As on can see, the gaps have disapeared and the statistics is much better, except on the border were only one image contributes to the integrated image.

Conclusion

The multi_geometry module of pyFAI makes powder diffraction experiments with small moving detectors much easier.

Some people would like to stitch input images together prior to integration. There are plenty of good tools to do this: generalist one like Photoshop or more specialized ones like AutoPano. More seriously this can be using the distortion module of a detector to re-sample the signal on a regular grid but one will have to store on one side the number of actual pixel contributing to a regular pixels and on the other the total intensity contained in the regularized pixel. Without the former information, doing science with a rebinned image is as meaningful as using Photoshop.