Extracting ellipse parmeters from rings

During a powder diffraction experiment, the scattering occures along cconcentric cones, originating from the sample position and named after 2 famous scientists: Debye and Scherrer.

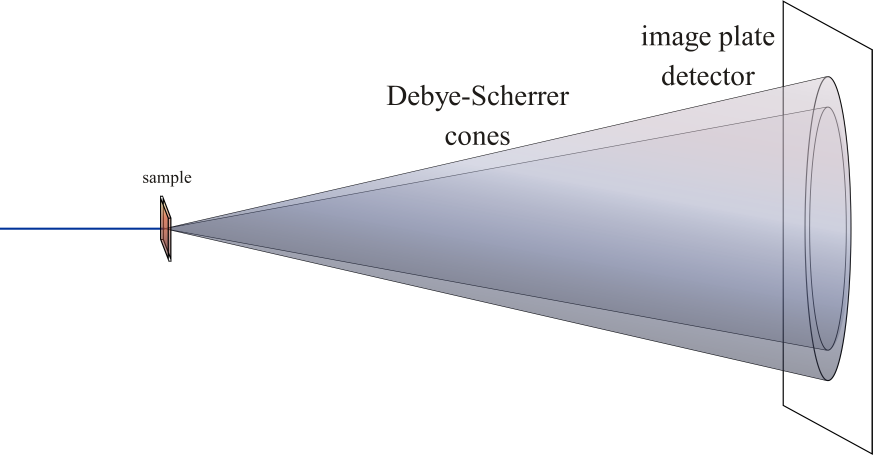
Those cones are intersected by the detector and all the calibration step in pyFAI comes down is fitting the “ring” seen on the detector into a meaningful experimental geometry.

In the most common case, a flat detector is mounted orthogonal to the incident beam and all pixel have the same size. The diffraction patern is then a set of concentric cercles. When the detector is still flat and all the pixels are the same but the mounting may be a bit off, or maybe for other technical reason one gets a set of concentric ellipses. This procedures explains how to extract the center coordinates, axis lengths and orientation.

The code in pyFAI is heavily inspired from: http://nicky.vanforeest.com/misc/fitEllipse/fitEllipse.html It uses a SVD decomposition in a similar way to the Wolfgang Kabsch’s algorithm (1976) to retrieve the best ellipse fitting all point without actually performing a fit.

%matplotlib inline

from matplotlib import pyplot
from pyFAI.utils.ellipse import fit_ellipse
import inspect
print(inspect.getsource(fit_ellipse))

def fit_ellipse(pty, ptx, _allow_delta=True):
    """Fit an ellipse

    inspired from
    http://nicky.vanforeest.com/misc/fitEllipse/fitEllipse.html

    :param pty: point coordinates in the slow dimension (y)
    :param ptx: point coordinates in the fast dimension (x)
    :raise ValueError: If the ellipse can't be fitted
    """
    x = ptx[:, numpy.newaxis]
    y = pty[:, numpy.newaxis]
    D = numpy.hstack((x * x, x * y, y * y, x, y, numpy.ones_like(x)))
    S = numpy.dot(D.T, D)
    try:
        inv = numpy.linalg.inv(S)
    except numpy.linalg.LinAlgError:
        if not _allow_delta:
            raise ValueError("Ellipse can't be fitted")
        # Try to do the same with a delta
        delta = 100
        ellipse = fit_ellipse(pty + delta, ptx + delta, _allow_delta=False)
        y0, x0, angle, wlong, wshort = ellipse
        return Ellipse(y0 - delta, x0 - delta, angle, wlong, wshort)

    C = numpy.zeros([6, 6])
    C[0, 2] = C[2, 0] = 2
    C[1, 1] = -1
    E, V = numpy.linalg.eig(numpy.dot(inv, C))
    m = numpy.logical_and(numpy.isfinite(E), numpy.isreal(E))
    E, V = E[m], V[:, m]
    n = numpy.argmax(E) if E.max() > 0 else numpy.argmin(E)
    res = V[:, n]
    b, c, d, f, g, a = res[1] / 2, res[2], res[3] / 2, res[4] / 2, res[5], res[0]
    num = b * b - a * c
    x0 = (c * d - b * f) / num
    y0 = (a * f - b * d) / num
    if b == 0:
        if a > c:
            angle = 0
        else:
            angle = pi / 2
    else:
        if a > c:
            angle = atan2(2 * b, (a - c)) / 2
        else:
            angle = numpy.pi / 2 + atan2(2 * b, (a - c)) / 2
    up = 2 * (a * f * f + c * d * d + g * b * b - 2 * b * d * f - a * c * g)
    down1 = (b * b - a * c) * ((c - a) * sqrt(1 + 4 * b * b / ((a - c) * (a - c))) - (c + a))
    down2 = (b * b - a * c) * ((a - c) * sqrt(1 + 4 * b * b / ((a - c) * (a - c))) - (c + a))

    a2 = up / down1
    b2 = up / down2
    if a2 < 0 or b2 < 0:
        raise ValueError("Ellipse can't be fitted")

    res1 = numpy.sqrt(a2)
    res2 = numpy.sqrt(b2)
    return Ellipse(y0, x0, angle, max(res1, res2), min(res1, res2))

from matplotlib import patches
from numpy import rad2deg

def display(ptx, pty, ellipse=None):
    """A function to overlay a set of points and the calculated ellipse
    """
    fig = pyplot.figure()
    ax = fig.add_subplot(111)
    if ellipse is not None:
        error = False
        y0, x0, angle, wlong, wshort = ellipse
        if wshort == 0:
            error = True
            wshort = 0.0001
        if wlong == 0:
            error = True
            wlong = 0.0001
        patch = patches.Arc((x0, y0), width=wlong*2, height=wshort*2, angle=rad2deg(angle))
        if error:
            patch.set_color("red")
        else:
            patch.set_color("green")
        ax.add_patch(patch)

        bbox = patch.get_window_extent()
        ylim = min(y0 - wlong, pty.min()), max(y0 + wlong, pty.max())
        xlim = min(x0 - wlong, ptx.min()), max(x0 - wlong, ptx.max())
    else:
        ylim = pty.min(), pty.max()
        xlim = ptx.min(), ptx.max()
    ax.plot(ptx, pty, "ro", color="blue")
    ax.set_xlim(*xlim)
    ax.set_ylim(*ylim)
    pyplot.show()

from numpy import sin, cos, random, pi, linspace
arc = 0.8
npt = 100
R = linspace(0, arc * pi, npt)
ptx = 1.5 * cos(R) + 2 + random.normal(scale=0.05, size=npt)
pty = sin(R) + 1. + random.normal(scale=0.05, size=npt)

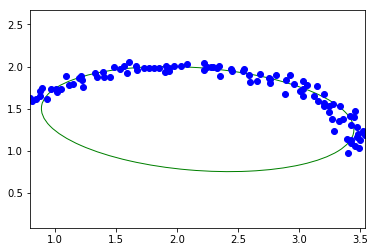
ellipse = fit_ellipse(pty, ptx)
print(ellipse)
display(ptx, pty, ellipse)

Ellipse(center_1=1.37812524025027, center_2=2.1702755528814146, angle=-0.1246970791733077, half_long_axis=1.289027842116212, half_short_axis=0.6066722714141386)

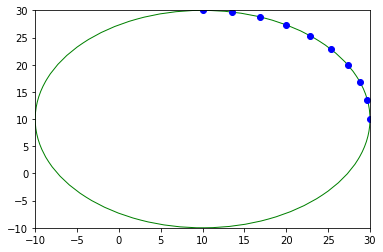
angles = linspace(0, pi / 2, 10)
pty = sin(angles) * 20 + 10
ptx = cos(angles) * 20 + 10
ellipse = fit_ellipse(pty, ptx)
print(ellipse)
display(ptx, pty, ellipse)

Ellipse(center_1=10.000000000332909, center_2=10.000000000325038, angle=2.3689992424085746, half_long_axis=19.999999999804693, half_short_axis=19.999999999532037)

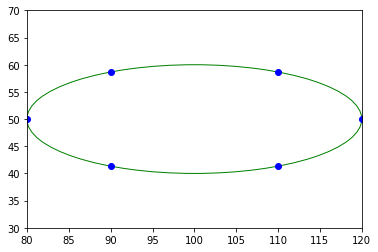
angles = linspace(0, pi * 2, 6, endpoint=False)
pty = sin(angles) * 10 + 50
ptx = cos(angles) * 20 + 100
ellipse = fit_ellipse(pty, ptx)
print(ellipse)
display(ptx, pty, ellipse)

Ellipse(center_1=50.000000000000576, center_2=100.0000000000018, angle=3.141592653589068, half_long_axis=19.999999999994646, half_short_axis=10.000000000002697)

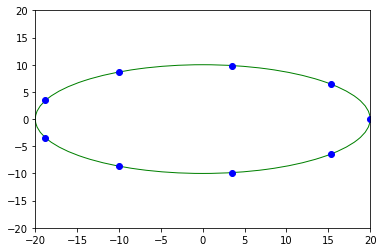
# Center to zero
angles = linspace(0, 2*pi, 9, endpoint=False)
pty = sin(angles) * 10 + 0
ptx = cos(angles) * 20 + 0
ellipse = fit_ellipse(pty, ptx)
print(ellipse)
display(ptx, pty, ellipse)

Ellipse(center_1=-5.030642569181509e-12, center_2=-8.540723683836404e-12, angle=1.6532775148903056e-11, half_long_axis=19.999999999815742, half_short_axis=10.00000000009243)

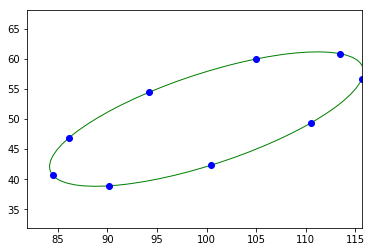
angles = linspace(0, 2 * pi, 9, endpoint=False)
pty = 50 + 10 * cos(angles) + 5 * sin(angles)
ptx = 100 + 5 * cos(angles) + 15 * sin(angles)
ellipse = fit_ellipse(pty, ptx)
print(ellipse)
display(ptx, pty, ellipse)

Ellipse(center_1=50.00000000000121, center_2=100.00000000000088, angle=0.5535743588955828, half_long_axis=18.09016994372895, half_short_axis=6.909830056258535)

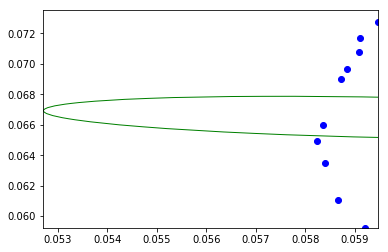
# Points from real peaking
from numpy import array
pty = array([0.06599215, 0.06105629, 0.06963708, 0.06900191, 0.06496001, 0.06352082, 0.05923421, 0.07080027, 0.07276284, 0.07170048])
ptx = array([0.05836343, 0.05866434, 0.05883284, 0.05872581, 0.05823667, 0.05839846, 0.0591999, 0.05907079, 0.05945377, 0.05909428])
try:
    ellipse = fit_ellipse(pty, ptx)
except Exception as e:
    ellipse = None
    print(e)
display(ptx, pty, ellipse)

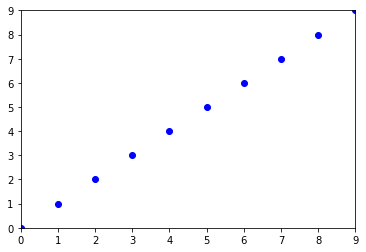
# Line
from numpy import arange
pty = arange(10)
ptx = arange(10)
try:
    ellipse = fit_ellipse(pty, ptx)
except Exception as e:
    ellipse = None
    print(e)
display(ptx, pty, ellipse)

Ellipse can't be fitted

Conclusion

Within pyFAI’s calibration process, the parameters of the ellipse are used in first instance as input guess for starting the fit procedure, which uses slsqp from scipy.optimize.