Extracting ellipse parmeters from rings

During a powder diffraction experiment, the scattering occures along cconcentric cones, originating from the sample position and named after 2 famous scientists: Debye and Scherrer.

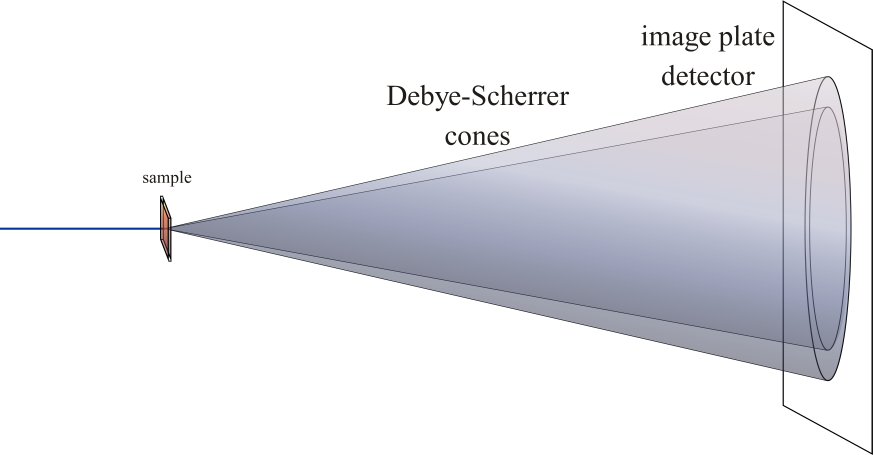
Those cones are intersected by the detector and all the calibration step in pyFAI comes down is fitting the “ring” seen on the detector into a meaningful experimental geometry.

In the most common case, a flat detector is mounted orthogonal to the incident beam and all pixel have the same size. The diffraction patern is then a set of concentric cercles. When the detector is still flat and all the pixels are the same but the mounting may be a bit off, or maybe for other technical reason one gets a set of concentric ellipses. This procedures explains how to extract the center coordinates, axis lengths and orientation.

The code in pyFAI is heavily inspired from: https://github.com/ndvanforeest/fit_ellipse It uses a SVD decomposition in a similar way to the Wolfgang Kabsch’s algorithm (1976) to retrieve the best ellipse fitting all point without actually performing a fit.

%matplotlib inline

import sys
sys.path.insert(0,"/home/jerome/workspace-ssd/pyFAI/build/lib.linux-x86_64-3.9/")
from matplotlib import pyplot
from pyFAI.utils.ellipse import fit_ellipse
import inspect
print(inspect.getsource(fit_ellipse))

def fit_ellipse(pty, ptx, _allow_delta=True):
    """Fit an ellipse

    Math from
    https://mathworld.wolfram.com/Ellipse.html #15

    inspired from
    http://nicky.vanforeest.com/misc/fitEllipse/fitEllipse.html

    :param pty: point coordinates in the slow dimension (y)
    :param ptx: point coordinates in the fast dimension (x)
    :raise ValueError: If the ellipse can't be fitted
    """
    x = ptx[:, numpy.newaxis]
    y = pty[:, numpy.newaxis]
    D = numpy.hstack((x * x, x * y, y * y, x, y, numpy.ones_like(x)))
    S = numpy.dot(D.T, D)
    try:
        inv = numpy.linalg.inv(S)
    except numpy.linalg.LinAlgError:
        if not _allow_delta:
            raise ValueError("Ellipse can't be fitted: singular matrix")
        # Try to do the same with a delta
        delta = 100
        ellipse = fit_ellipse(pty + delta, ptx + delta, _allow_delta=False)
        y0, x0, angle, wlong, wshort = ellipse
        return Ellipse(y0 - delta, x0 - delta, angle, wlong, wshort)

    C = numpy.zeros([6, 6])
    C[0, 2] = C[2, 0] = 2
    C[1, 1] = -1
    E, V = numpy.linalg.eig(numpy.dot(inv, C))

    # First of all, sieve out all infinite and complex eigenvalues and come back to the Real world
    m = numpy.logical_and(numpy.isfinite(E), numpy.isreal(E))
    E, V = E[m].real, V[:, m].real

    # Ensures a>0, invert eigenvectors concerned
    V[:, V[0] < 0] = -V[:, V[0] < 0]
    # See https://mathworld.wolfram.com/Ellipse.html #15
    # Eigenvector must meet constraint (ac - b^2)>0 to be valid.
    A = V[0]
    B = V[1] / 2.0
    C = V[2]
    D = V[3] / 2.0
    F = V[4] / 2.0
    G = V[5]

    # Condition 1: Delta = det((a b d)(b c f)(d f g)) !=0
    Delta = A * (C * G - F * F) - G * B * B + D * (2 * B * F - C * D)
    # Condition 2: J>0
    J = (A * C - B * B)

    # Condition 3: Delta/(A+C)<0, replaces by Delta*(A+C)<0, less warnings
    m = numpy.logical_and(J > 0, Delta != 0)
    m = numpy.logical_and(m, Delta * (A + C) < 0)

    n = numpy.where(m)[0]
    if len(n) == 0:
        raise ValueError("Ellipse can't be fitted: No Eigenvalue match all 3 criteria")
    else:
        n = n[0]
    a = A[n]
    b = B[n]
    c = C[n]
    d = D[n]
    f = F[n]
    g = G[n]
#     print(f"a {a}, b {b}, c {c}, ac-b² {a*c - b*b}")

    # Calculation of the center:
    denom = b * b - a * c
    x0 = (c * d - b * f) / denom
    y0 = (a * f - b * d) / denom

    up = 2 * (a * f * f + c * d * d + g * b * b - 2 * b * d * f - a * c * g)
    down1 = (b * b - a * c) * ((c - a) * sqrt(1 + 4 * b * b / ((a - c) * (a - c))) - (c + a))
    down2 = (b * b - a * c) * ((a - c) * sqrt(1 + 4 * b * b / ((a - c) * (a - c))) - (c + a))
#     print(f"up {up}, down1 {down1}, down2 {down2}")
    a2 = up / down1
    b2 = up / down2
    if a2 <= 0 or b2 <= 0:
        raise ValueError("Ellipse can't be fitted, negative sqrt")

    res1 = sqrt(a2)
    res2 = sqrt(b2)

    if a == c:
        angle = 0  # we have a circle
    elif res2 > res1:
        res1, res2 = res2, res1
        angle = 0.5 * (pi + atan2(2 * b, (a - c)))
    else:
        angle = 0.5 * (pi + atan2(2 * b, (a - c)))
    return Ellipse(y0, x0, angle, res1, res2)

from matplotlib import patches
from numpy import rad2deg

def display(ptx, pty, ellipse=None):
    """A function to overlay a set of points and the calculated ellipse
    """
    fig = pyplot.figure()
    ax = fig.add_subplot(111)
    if ellipse is not None:
        error = False
        y0, x0, angle, wlong, wshort = ellipse
        if wshort == 0:
            error = True
            wshort = 0.0001
        if wlong == 0:
            error = True
            wlong = 0.0001
        patch = patches.Arc((x0, y0), width=wlong*2, height=wshort*2, angle=rad2deg(angle))
        if error:
            patch.set_color("red")
        else:
            patch.set_color("green")
        ax.add_patch(patch)

        bbox = patch.get_window_extent()
        ylim = min(y0 - wlong, pty.min()), max(y0 + wlong, pty.max())
        xlim = min(x0 - wlong, ptx.min()), max(x0 - wlong, ptx.max())
    else:
        ylim = pty.min(), pty.max()
        xlim = ptx.min(), ptx.max()
    ax.plot(ptx, pty, "ro", color="blue")
    ax.set_xlim(*xlim)
    ax.set_ylim(*ylim)
    pyplot.show()

from numpy import sin, cos, random, pi, linspace
arc = 0.8
npt = 100
R = linspace(0, arc * pi, npt)
ptx = 1.5 * cos(R) + 2 + random.normal(scale=0.05, size=npt)
pty = sin(R) + 1. + random.normal(scale=0.05, size=npt)

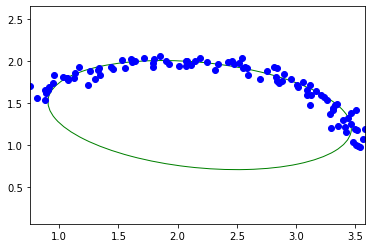
ellipse = fit_ellipse(pty, ptx)
print(ellipse)
display(ptx, pty, ellipse)

Ellipse(center_1=1.3541199392478749, center_2=2.185507522307149, angle=2.9807976434722416, half_long_axis=1.293119256631015, half_short_axis=0.6228734407617278)

angles = linspace(0, pi / 2, 10)
pty = sin(angles) * 20 + 10
ptx = cos(angles) * 20 + 10
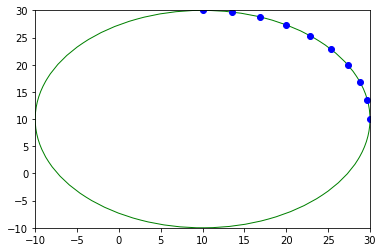
ellipse = fit_ellipse(pty, ptx)
print(ellipse)
display(ptx, pty, ellipse)

Ellipse(center_1=10.000000000332909, center_2=10.000000000325038, angle=2.3689992424085746, half_long_axis=19.999999999804693, half_short_axis=19.999999999532037)

angles = linspace(0, pi * 2, 6, endpoint=False)
pty = sin(angles) * 10 + 50
ptx = cos(angles) * 20 + 100
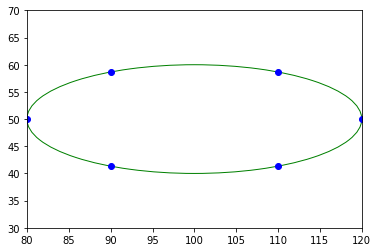
ellipse = fit_ellipse(pty, ptx)
print(ellipse)
display(ptx, pty, ellipse)

Ellipse(center_1=50.000000000000576, center_2=100.0000000000018, angle=3.141592653589068, half_long_axis=19.999999999994646, half_short_axis=10.000000000002697)

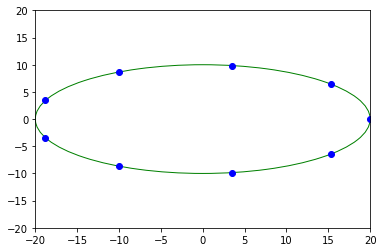
# Center to zero
angles = linspace(0, 2*pi, 9, endpoint=False)
pty = sin(angles+0) * 10 + 0
ptx = cos(angles+0) * 20 + 0
ellipse = fit_ellipse(pty, ptx)
print(ellipse)
display(ptx, pty, ellipse)

Ellipse(center_1=-5.030642569181509e-12, center_2=-8.540723683836404e-12, angle=1.6532775148903056e-11, half_long_axis=19.999999999815742, half_short_axis=10.00000000009243)

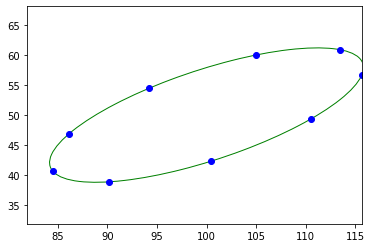
angles = linspace(0, 2 * pi, 9, endpoint=False)
pty = 50 + 10 * cos(angles) + 5 * sin(angles)
ptx = 100 + 5 * cos(angles) + 15 * sin(angles)
ellipse = fit_ellipse(pty, ptx)
print(ellipse)
display(ptx, pty, ellipse)

Ellipse(center_1=50.00000000000121, center_2=100.00000000000088, angle=0.5535743588955828, half_long_axis=18.09016994372895, half_short_axis=6.909830056258535)

# Points from real peaking
from numpy import array
pty = array([0.06599215, 0.06105629, 0.06963708, 0.06900191, 0.06496001, 0.06352082, 0.05923421, 0.07080027, 0.07276284, 0.07170048])
ptx = array([0.05836343, 0.05866434, 0.05883284, 0.05872581, 0.05823667, 0.05839846, 0.0591999, 0.05907079, 0.05945377, 0.05909428])
try:
    ellipse = fit_ellipse(pty, ptx)
except Exception as e:
    ellipse = None
    print(e)
display(ptx, pty, ellipse)

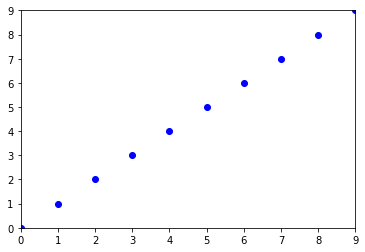
# Line
from numpy import arange
pty = arange(10)
ptx = arange(10)
try:
    ellipse = fit_ellipse(pty, ptx)
except Exception as e:
    ellipse = None
    print(e)
display(ptx, pty, ellipse)

Ellipse can't be fitted: singular matrix

Conclusion

Within pyFAI’s calibration process, the parameters of the ellipse are used in first instance as input guess for starting the fit procedure, which uses slsqp from scipy.optimize.