Parallel processing of a stack of data stored in HDF5 with multi-threading
This tutorial explains how it is possible to treat in parallel a large HDF5 dataset which does not fit into the computer memory.
For this tutorial, a very recent version of pyFAI is needed, newer than summer 2022. It demonstrates features wich will only be available in release 0.22.
This tutorial expains how to take benefit from multi-threading. This framework is not very popular in the Python world due to the Global Interpreter Lock (GIL), but properly written C-code which does release the GIL can be very fast, sometimes as fast as GPU code (on large computers).
Credits:
Thomas Vincent (ESRF) for the parallel decompression of HDF5 chunks and the Jupyter-slurm
Pierre Paleo (ESRF) for struggling with this kind of stuff with GPUs
Jon Wright (ESRF) for the CSC integrator, while implemented in serial is multithreading friendly
The French-CRG for providing a manycore computer (2 x 32-core AMD EPYC 75F3)
Nota: No GPU is needed for this tutorial!
Important: the bitshuffle module needs to be compiled without OpenMP, since the tutorial aims at demonstrating that Python threads can be almost as efficient as OpenMP. If you have a doubt about OpenMP, please uncomment the environment variable OMP_NUM_THREADS reset in the second cell. This will unfortunately bias the performance measurement of pyFAI with the CSR sparse-matrix multiplication.
[1]:
%matplotlib inline
# use `widget` for better user experience; `inline` is for documentation generation
[2]:
import sys, os, collections, struct, time
# Ensure OpenMP is disabled
# os.environ["OMP_NUM_THREADS"] = "1"
import numpy, pyFAI
import h5py, hdf5plugin
from queue import Queue
import threading
import bitshuffle
from matplotlib.pyplot import subplots
start_time = time.time()
Item = collections.namedtuple("Item", "index data")
[3]:
nbthreads = len(os.sched_getaffinity(0))
print(f"Working with {nbthreads} threads. Mind OpenMP needs to be disabled in the bitshuffle code !")
Working with 64 threads. Mind OpenMP needs to be disabled in the bitshuffle code !
[4]:
!lscpu
Architecture: x86_64
CPU op-mode(s): 32-bit, 64-bit
Byte Order: Little Endian
Address sizes: 48 bits physical, 48 bits virtual
CPU(s): 64
On-line CPU(s) list: 0-63
Thread(s) per core: 1
Core(s) per socket: 32
Socket(s): 2
NUMA node(s): 2
Vendor ID: AuthenticAMD
CPU family: 25
Model: 1
Model name: AMD EPYC 75F3 32-Core Processor
Stepping: 1
Frequency boost: enabled
CPU MHz: 1477.966
CPU max MHz: 2950.0000
CPU min MHz: 1500.0000
BogoMIPS: 5888.80
Virtualization: AMD-V
L1d cache: 2 MiB
L1i cache: 2 MiB
L2 cache: 32 MiB
L3 cache: 512 MiB
NUMA node0 CPU(s): 0-31
NUMA node1 CPU(s): 32-63
Vulnerability Itlb multihit: Not affected
Vulnerability L1tf: Not affected
Vulnerability Mds: Not affected
Vulnerability Meltdown: Not affected
Vulnerability Mmio stale data: Not affected
Vulnerability Spec store bypass: Mitigation; Speculative Store Bypass disabled v
ia prctl and seccomp
Vulnerability Spectre v1: Mitigation; usercopy/swapgs barriers and __user
pointer sanitization
Vulnerability Spectre v2: Mitigation; Retpolines, IBPB conditional, IBRS_
FW, STIBP disabled, RSB filling
Vulnerability Srbds: Not affected
Vulnerability Tsx async abort: Not affected
Flags: fpu vme de pse tsc msr pae mce cx8 apic sep mtr
r pge mca cmov pat pse36 clflush mmx fxsr sse s
se2 ht syscall nx mmxext fxsr_opt pdpe1gb rdtsc
p lm constant_tsc rep_good nopl nonstop_tsc cpu
id extd_apicid aperfmperf pni pclmulqdq monitor
ssse3 fma cx16 pcid sse4_1 sse4_2 x2apic movbe
popcnt aes xsave avx f16c rdrand lahf_lm cmp_l
egacy svm extapic cr8_legacy abm sse4a misalign
sse 3dnowprefetch osvw ibs skinit wdt tce topoe
xt perfctr_core perfctr_nb bpext perfctr_llc mw
aitx cpb cat_l3 cdp_l3 invpcid_single hw_pstate
ssbd mba ibrs ibpb stibp vmmcall fsgsbase bmi1
avx2 smep bmi2 invpcid cqm rdt_a rdseed adx sm
ap clflushopt clwb sha_ni xsaveopt xsavec xgetb
v1 xsaves cqm_llc cqm_occup_llc cqm_mbm_total c
qm_mbm_local clzero irperf xsaveerptr wbnoinvd
arat npt lbrv svm_lock nrip_save tsc_scale vmcb
_clean flushbyasid decodeassists pausefilter pf
threshold v_vmsave_vmload vgif umip pku ospke v
aes vpclmulqdq rdpid overflow_recov succor smca
Setup the enviroment:
This is a purely virtual experiment, we will use an Eiger 4M detector with data integrated over 1000 bins. Those parameters can be tuned.
Random data are generated, to keep this file fairly small, it is generated with small numbers which compress nicely. The speed of the drive where you will put the file is likely to have a huge impact !
[5]:
det = pyFAI.detector_factory("eiger_4M")
shape = det.shape
dtype = numpy.dtype("uint32")
filename = "/tmp/big.h5"
nbins = 1000
cmp = hdf5plugin.Bitshuffle()
hdf5plugin.config
[5]:
HDF5PluginBuildOptions(openmp=False, native=False, sse2=True, avx2=False, cpp11=True, filter_file_extension='.so')
[6]:
mem_bytes = os.sysconf('SC_PAGE_SIZE') * os.sysconf('SC_PHYS_PAGES')
print(f"Number of frames the computer can host in memory: {mem_bytes/(numpy.prod(shape)*dtype.itemsize):.3f}")
if os.environ.get('SLURM_MEM_PER_NODE'):
print(f"Number of frames the computer can host in memory with SLURM restrictions: {int(os.environ['SLURM_MEM_PER_NODE'])*(1<<20)/(numpy.prod(shape)*dtype.itemsize):.3f}")
Number of frames the computer can host in memory: 30127.704
Number of frames the computer can host in memory with SLURM restrictions: 3829.928
[7]:
#The computer being limited to 64G of RAM, the number of frames actually possible is 3800.
nbframes = 4096 # slightly larger than the maximum achievable ! Such a dataset should not host in memory.
[8]:
#Prepare a frame with little count so that it compresses well
geo = {"detector": det,
"wavelength": 1e-10,
"rot3":0} #work around a bug https://github.com/silx-kit/pyFAI/pull/1749
ai = pyFAI.load(geo)
q = numpy.arange(15)
img = ai.calcfrom1d(q, 100/(1+q*q))
frame = numpy.random.poisson(img).astype(dtype)
[9]:
# display the image
fig,ax = subplots()
ax.imshow(frame)
[9]:
<matplotlib.image.AxesImage at 0x14e68fca2f40>

[10]:
print("Performances of the different algorithms for azimuthal integration of Eiger 4M image")
for algo in ("histogram", "csc", "csr"):
print(f"Using algorithm {algo:10s}:", end=" ")
%timeit ai.integrate1d(img, nbins, method=("full", algo, "cython"))
Performances of the different algorithms for azimuthal integration of Eiger 4M image
Using algorithm histogram : 434 ms ± 18.9 ms per loop (mean ± std. dev. of 7 runs, 1 loop each)
Using algorithm csc : 38.5 ms ± 252 µs per loop (mean ± std. dev. of 7 runs, 1 loop each)
Using algorithm csr : 51.1 ms ± 8.2 ms per loop (mean ± std. dev. of 7 runs, 1 loop each)
Note: The full pixel splitting is time consuming and handicaps the histogram algorithm while both sparse-matrix methods are much faster since they cache this calculation in the sparse matrix.
The compared performances of sparse-matrix methods is rather surprizing since the CSC algorithm, single threaded, is faster than the CSR which runs in parallel over 2x32 cores. This result is the combination of two facotors:
The computer is built with two processors/sockets controling each its own memory. We call this a Non Uniform Memory Access computer and can be checked with
numactrl --hardware. The CSR matrix multiplication will dispatch work on both processors and thus, needs to transfer part of the image from one NUMA subsystem (socket) to the other, which is slow (3.2x slower compared to a single-socket access, according to the output of numactl).The very large cache of this processor: 512MB are reported by
lscpu, but a more precise tool,lstopodescribes them as 32MB of L3 cache shared between 4 cores. This very large cache allows the complete frame and the sparse matrix to be pre-fetched which is a great advantage for the CSC algorithm.
Running the very same benchmark on an Intel 2-socket server would remove the point 2, while running on a singe socket intel workstation would remove both points and the normal results would be that CSR should be faster than CSC. The best performances on can get with the CSR algorithm should be obtained when using 4 cores (sharing the same cache L3) out of 64 on this computer. This can be done by setting the environment variable OMP_NUM_THREADS. Unfortunately, it also requires to restart the process, thus cannot be demonstrated easily in the notebook (without restarting).
The first message to take home is that without the knownledge of the actual computer, no high-performace computing is possible
[11]:
!numactl --hardware
available: 2 nodes (0-1)
node 0 cpus: 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31
node 0 size: 257524 MB
node 0 free: 222966 MB
node 1 cpus: 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63
node 1 size: 258006 MB
node 1 free: 247449 MB
node distances:
node 0 1
0: 10 32
1: 32 10
[12]:
!lstopo --of console
Machine (503GB total)
Package L#0
NUMANode L#0 (P#0 251GB)
L3 L#0 (32MB)
L2 L#0 (512KB) + L1d L#0 (32KB) + L1i L#0 (32KB) + Core L#0 + PU L#0 (P#0)
L2 L#1 (512KB) + L1d L#1 (32KB) + L1i L#1 (32KB) + Core L#1 + PU L#1 (P#1)
L2 L#2 (512KB) + L1d L#2 (32KB) + L1i L#2 (32KB) + Core L#2 + PU L#2 (P#2)
L2 L#3 (512KB) + L1d L#3 (32KB) + L1i L#3 (32KB) + Core L#3 + PU L#3 (P#3)
L3 L#1 (32MB)
L2 L#4 (512KB) + L1d L#4 (32KB) + L1i L#4 (32KB) + Core L#4 + PU L#4 (P#4)
L2 L#5 (512KB) + L1d L#5 (32KB) + L1i L#5 (32KB) + Core L#5 + PU L#5 (P#5)
L2 L#6 (512KB) + L1d L#6 (32KB) + L1i L#6 (32KB) + Core L#6 + PU L#6 (P#6)
L2 L#7 (512KB) + L1d L#7 (32KB) + L1i L#7 (32KB) + Core L#7 + PU L#7 (P#7)
L3 L#2 (32MB)
L2 L#8 (512KB) + L1d L#8 (32KB) + L1i L#8 (32KB) + Core L#8 + PU L#8 (P#8)
L2 L#9 (512KB) + L1d L#9 (32KB) + L1i L#9 (32KB) + Core L#9 + PU L#9 (P#9)
L2 L#10 (512KB) + L1d L#10 (32KB) + L1i L#10 (32KB) + Core L#10 + PU L#10 (P#10)
L2 L#11 (512KB) + L1d L#11 (32KB) + L1i L#11 (32KB) + Core L#11 + PU L#11 (P#11)
L3 L#3 (32MB)
L2 L#12 (512KB) + L1d L#12 (32KB) + L1i L#12 (32KB) + Core L#12 + PU L#12 (P#12)
L2 L#13 (512KB) + L1d L#13 (32KB) + L1i L#13 (32KB) + Core L#13 + PU L#13 (P#13)
L2 L#14 (512KB) + L1d L#14 (32KB) + L1i L#14 (32KB) + Core L#14 + PU L#14 (P#14)
L2 L#15 (512KB) + L1d L#15 (32KB) + L1i L#15 (32KB) + Core L#15 + PU L#15 (P#15)
L3 L#4 (32MB)
L2 L#16 (512KB) + L1d L#16 (32KB) + L1i L#16 (32KB) + Core L#16 + PU L#16 (P#16)
L2 L#17 (512KB) + L1d L#17 (32KB) + L1i L#17 (32KB) + Core L#17 + PU L#17 (P#17)
L2 L#18 (512KB) + L1d L#18 (32KB) + L1i L#18 (32KB) + Core L#18 + PU L#18 (P#18)
L2 L#19 (512KB) + L1d L#19 (32KB) + L1i L#19 (32KB) + Core L#19 + PU L#19 (P#19)
L3 L#5 (32MB)
L2 L#20 (512KB) + L1d L#20 (32KB) + L1i L#20 (32KB) + Core L#20 + PU L#20 (P#20)
L2 L#21 (512KB) + L1d L#21 (32KB) + L1i L#21 (32KB) + Core L#21 + PU L#21 (P#21)
L2 L#22 (512KB) + L1d L#22 (32KB) + L1i L#22 (32KB) + Core L#22 + PU L#22 (P#22)
L2 L#23 (512KB) + L1d L#23 (32KB) + L1i L#23 (32KB) + Core L#23 + PU L#23 (P#23)
L3 L#6 (32MB)
L2 L#24 (512KB) + L1d L#24 (32KB) + L1i L#24 (32KB) + Core L#24 + PU L#24 (P#24)
L2 L#25 (512KB) + L1d L#25 (32KB) + L1i L#25 (32KB) + Core L#25 + PU L#25 (P#25)
L2 L#26 (512KB) + L1d L#26 (32KB) + L1i L#26 (32KB) + Core L#26 + PU L#26 (P#26)
L2 L#27 (512KB) + L1d L#27 (32KB) + L1i L#27 (32KB) + Core L#27 + PU L#27 (P#27)
L3 L#7 (32MB)
L2 L#28 (512KB) + L1d L#28 (32KB) + L1i L#28 (32KB) + Core L#28 + PU L#28 (P#28)
L2 L#29 (512KB) + L1d L#29 (32KB) + L1i L#29 (32KB) + Core L#29 + PU L#29 (P#29)
L2 L#30 (512KB) + L1d L#30 (32KB) + L1i L#30 (32KB) + Core L#30 + PU L#30 (P#30)
L2 L#31 (512KB) + L1d L#31 (32KB) + L1i L#31 (32KB) + Core L#31 + PU L#31 (P#31)
HostBridge
PCIBridge
PCI 01:00.0 (RAID)
Block(Disk) "sdb"
Block(Disk) "sda"
HostBridge
PCIBridge
PCI 63:00.0 (Ethernet)
Net "eno12399np0"
PCI 63:00.1 (Ethernet)
Net "eno12409np1"
PCIBridge
PCIBridge
PCI 62:00.0 (VGA)
Package L#1
NUMANode L#1 (P#1 252GB)
L3 L#8 (32MB)
L2 L#32 (512KB) + L1d L#32 (32KB) + L1i L#32 (32KB) + Core L#32 + PU L#32 (P#32)
L2 L#33 (512KB) + L1d L#33 (32KB) + L1i L#33 (32KB) + Core L#33 + PU L#33 (P#33)
L2 L#34 (512KB) + L1d L#34 (32KB) + L1i L#34 (32KB) + Core L#34 + PU L#34 (P#34)
L2 L#35 (512KB) + L1d L#35 (32KB) + L1i L#35 (32KB) + Core L#35 + PU L#35 (P#35)
L3 L#9 (32MB)
L2 L#36 (512KB) + L1d L#36 (32KB) + L1i L#36 (32KB) + Core L#36 + PU L#36 (P#36)
L2 L#37 (512KB) + L1d L#37 (32KB) + L1i L#37 (32KB) + Core L#37 + PU L#37 (P#37)
L2 L#38 (512KB) + L1d L#38 (32KB) + L1i L#38 (32KB) + Core L#38 + PU L#38 (P#38)
L2 L#39 (512KB) + L1d L#39 (32KB) + L1i L#39 (32KB) + Core L#39 + PU L#39 (P#39)
L3 L#10 (32MB)
L2 L#40 (512KB) + L1d L#40 (32KB) + L1i L#40 (32KB) + Core L#40 + PU L#40 (P#40)
L2 L#41 (512KB) + L1d L#41 (32KB) + L1i L#41 (32KB) + Core L#41 + PU L#41 (P#41)
L2 L#42 (512KB) + L1d L#42 (32KB) + L1i L#42 (32KB) + Core L#42 + PU L#42 (P#42)
L2 L#43 (512KB) + L1d L#43 (32KB) + L1i L#43 (32KB) + Core L#43 + PU L#43 (P#43)
L3 L#11 (32MB)
L2 L#44 (512KB) + L1d L#44 (32KB) + L1i L#44 (32KB) + Core L#44 + PU L#44 (P#44)
L2 L#45 (512KB) + L1d L#45 (32KB) + L1i L#45 (32KB) + Core L#45 + PU L#45 (P#45)
L2 L#46 (512KB) + L1d L#46 (32KB) + L1i L#46 (32KB) + Core L#46 + PU L#46 (P#46)
L2 L#47 (512KB) + L1d L#47 (32KB) + L1i L#47 (32KB) + Core L#47 + PU L#47 (P#47)
L3 L#12 (32MB)
L2 L#48 (512KB) + L1d L#48 (32KB) + L1i L#48 (32KB) + Core L#48 + PU L#48 (P#48)
L2 L#49 (512KB) + L1d L#49 (32KB) + L1i L#49 (32KB) + Core L#49 + PU L#49 (P#49)
L2 L#50 (512KB) + L1d L#50 (32KB) + L1i L#50 (32KB) + Core L#50 + PU L#50 (P#50)
L2 L#51 (512KB) + L1d L#51 (32KB) + L1i L#51 (32KB) + Core L#51 + PU L#51 (P#51)
L3 L#13 (32MB)
L2 L#52 (512KB) + L1d L#52 (32KB) + L1i L#52 (32KB) + Core L#52 + PU L#52 (P#52)
L2 L#53 (512KB) + L1d L#53 (32KB) + L1i L#53 (32KB) + Core L#53 + PU L#53 (P#53)
L2 L#54 (512KB) + L1d L#54 (32KB) + L1i L#54 (32KB) + Core L#54 + PU L#54 (P#54)
L2 L#55 (512KB) + L1d L#55 (32KB) + L1i L#55 (32KB) + Core L#55 + PU L#55 (P#55)
L3 L#14 (32MB)
L2 L#56 (512KB) + L1d L#56 (32KB) + L1i L#56 (32KB) + Core L#56 + PU L#56 (P#56)
L2 L#57 (512KB) + L1d L#57 (32KB) + L1i L#57 (32KB) + Core L#57 + PU L#57 (P#57)
L2 L#58 (512KB) + L1d L#58 (32KB) + L1i L#58 (32KB) + Core L#58 + PU L#58 (P#58)
L2 L#59 (512KB) + L1d L#59 (32KB) + L1i L#59 (32KB) + Core L#59 + PU L#59 (P#59)
L3 L#15 (32MB)
L2 L#60 (512KB) + L1d L#60 (32KB) + L1i L#60 (32KB) + Core L#60 + PU L#60 (P#60)
L2 L#61 (512KB) + L1d L#61 (32KB) + L1i L#61 (32KB) + Core L#61 + PU L#61 (P#61)
L2 L#62 (512KB) + L1d L#62 (32KB) + L1i L#62 (32KB) + Core L#62 + PU L#62 (P#62)
L2 L#63 (512KB) + L1d L#63 (32KB) + L1i L#63 (32KB) + Core L#63 + PU L#63 (P#63)
HostBridge
PCIBridge
PCI c3:00.0 (SATA)
HostBridge
PCIBridge
PCI e1:00.0 (Ethernet)
Net "eno8303"
PCI e1:00.1 (Ethernet)
Net "eno8403"
[13]:
#Does not work unless one restarts the process
# print("Performances of the different algorithms for azimuthal integration of Eiger 4M image when using only 4 cores")
# mask = os.sched_getaffinity(0)
# os.sched_setaffinity(0, [0,1,2,3])
# for algo in ("histogram", "csc", "csr"):
# print(f"Using algorithm {algo}:", end=" ")
# %timeit ai.integrate1d(img, nbins, method=("full", algo, "cython"))
# os.sched_setaffinity(0, mask)
[14]:
%%timeit -r1 -n1 -o -q
#Saving of a HDF5 file with many frames ...
with h5py.File(filename, "w") as h:
ds = h.create_dataset("data", shape=(nbframes,)+shape, chunks=(1,)+shape, dtype=dtype, **cmp)
for i in range(nbframes):
ds[i] = frame + i%500 #Each frame has a different value to prevent caching effects
[14]:
<TimeitResult : 57.4 s ± 0 ns per loop (mean ± std. dev. of 1 run, 1 loop each)>
[15]:
timing_write = _
size=os.stat(filename).st_size
print(f"File size {size/(1024**3):.3f} GB with a compression ratio of {nbframes*numpy.prod(shape)*dtype.itemsize/size:.3f}x")
print(f"Write speed: {nbframes*numpy.prod(shape)*dtype.itemsize/(1e6*timing_write.best):.3f} MB/s of uncompressed data, or {nbframes/timing_write.best:.3f} fps.")
File size 9.241 GB with a compression ratio of 7.406x
Write speed: 1281.458 MB/s of uncompressed data, or 71.419 fps.
Reading all data from HDF5 file is as slow as, if not slower than, writing. This is mostly due to the decompression and to the many memory allocation performed.
[16]:
%%timeit -r1 -n1 -o -q
#Reading all frames and decompressing them
buffer = numpy.zeros(shape, dtype=dtype)
with h5py.File(filename, "r") as h:
ds = h["data"]
for i in range(nbframes):
ds.read_direct(buffer, numpy.s_[i,:,:], numpy.s_[:,:])
[16]:
<TimeitResult : 28.5 s ± 0 ns per loop (mean ± std. dev. of 1 run, 1 loop each)>
[17]:
timing_read1 = _
print(f"Read speed: {nbframes*numpy.prod(shape)*dtype.itemsize/(1e6*timing_read1.best):.3f} MB/s of uncompressed data, or {nbframes/timing_read1.best:.3f} fps.")
Read speed: 2581.492 MB/s of uncompressed data, or 143.874 fps.
[18]:
def decompress_bslz4_chunk(payload, dtype, chunk_shape):
"""This function decompresses ONE chunk with bitshuffle-LZ4.
The library needs to be compiled without OpenMP when using threads !
:param payload: string with the compressed data as read by h5py.
:param dtype: data type of the stored content
:param chunk_shape: shape of one chunk
:return: decompressed chunk"""
total_nbytes, block_nbytes = struct.unpack(">QI", payload[:12])
block_size = block_nbytes // dtype.itemsize
arr = numpy.frombuffer(payload, dtype=numpy.uint8, offset=12) # No copy here
chunk_data = bitshuffle.decompress_lz4(arr, chunk_shape, dtype, block_size)
return chunk_data
[19]:
%%timeit -r1 -n1 -o -q
#Reading all frames without decompressing them
with h5py.File(filename, "r") as h:
ds = h["data"]
for i in range(ds.id.get_num_chunks()):
filter_mask, chunk = ds.id.read_direct_chunk(ds.id.get_chunk_info(i).chunk_offset)
[19]:
<TimeitResult : 1.47 s ± 0 ns per loop (mean ± std. dev. of 1 run, 1 loop each)>
[20]:
timing_read2 = _
print(f"Read speed: {size/(1e6*timing_read2.best):.3f} MB/s of compressed data.")
print(f"HDF5 read speed (without decompression): {nbframes/timing_read2.best:.3f} fps.")
Read speed: 6727.893 MB/s of compressed data.
HDF5 read speed (without decompression): 2777.151 fps.
But the reading part data is fairly fast, if one does not decompress the data.
[21]:
#Decompression speed:
with h5py.File(filename, "r") as h:
ds = h["data"]
filter_mask, chunk = ds.id.read_direct_chunk(ds.id.get_chunk_info(1).chunk_offset)
print(f"Decompression speed of a single chunk/frame, filter_mask={filter_mask} should be null.")
timing_decompress = %timeit -r3 -o decompress_bslz4_chunk(chunk, dtype, shape)
print(f"The maximum decompression speed is {1/timing_decompress.best:.3f} fps, single threaded, \nand could reach {nbthreads/timing_decompress.best:.3f} fps in parallel over {nbthreads} threads.")
Decompression speed of a single chunk/frame, filter_mask=0 should be null.
8.3 ms ± 2.91 µs per loop (mean ± std. dev. of 3 runs, 100 loops each)
The maximum decompression speed is 120.520 fps, single threaded,
and could reach 7713.281 fps in parallel over 64 threads.
Prepare the azimuthal integrator
To allow the full parallelization of different integrators working in parallel, one must limit the number of Python call performed, this is why we need to extract the Cython integrator from AzimuthalIntegator. The integrator used here is a sparse matrix multiplication one with a CSC representation which is single-threaded. This engine is usually not the fastest but it is multitheading friendly.
[22]:
geo = {"detector": det,
"wavelength": 1e-10,
"rot3":0} #work around a bug https://github.com/silx-kit/pyFAI/pull/1749
ai = pyFAI.load(geo)
omega = ai.solidAngleArray()
res0 = ai.integrate1d(frame, nbins, method=("full", "csc", "cython"))
engine = ai.engines[res0.method].engine
#This is how the engine works:
res1 = engine.integrate_ng(frame, solidangle=omega)
assert numpy.allclose(res0.intensity, res1.intensity) # validates the equivalence of both approaches:
timing_integration = %timeit -r3 -o engine.integrate_ng(frame, solidangle=omega)
print(f"The maximum achievable integration speed on a single core is {1/timing_integration.best:.3f} fps which does not look fancy,\n\
but parallelized over {nbthreads} threads, it could reach: {nbthreads/timing_integration.best:.3f} fps!")
37.7 ms ± 157 µs per loop (mean ± std. dev. of 3 runs, 10 loops each)
The maximum achievable integration speed on a single core is 26.583 fps which does not look fancy,
but parallelized over 64 threads, it could reach: 1701.306 fps!
[23]:
%%timeit -o -r1 -n1 -q
#Naive implementation ... read+integrate
result0 = numpy.zeros((nbframes, nbins), dtype=numpy.float32)
method = ("full", "csr", "cython")
buffer = numpy.zeros(shape, dtype=dtype)
with h5py.File(filename, "r") as h:
ds = h["data"]
for i in range(nbframes):
ds.read_direct(buffer, numpy.s_[i,:,:], numpy.s_[:,:])
result0[i] = ai.integrate1d(buffer, nbins, method=method).intensity
[23]:
<TimeitResult : 3min 34s ± 0 ns per loop (mean ± std. dev. of 1 run, 1 loop each)>
[24]:
timing_naive = _
print(f"The maximum achievable decompression+integration speed is {1/(timing_decompress.best+timing_integration.best):.3f} fps in serial \n\
and {nbthreads*1/(timing_decompress.best+timing_integration.best):.3f} fps in parallel on {nbthreads} threads\n\
but a naive implementation provides only {nbframes/(timing_naive.best):.3f} fps.")
The maximum achievable decompression+integration speed is 21.779 fps in serial
and 1393.864 fps in parallel on 64 threads
but a naive implementation provides only 19.125 fps.
Effective implementation using multithreading:
One
readerwhich reads the dataset chunk-by-chunk and makes them available via an input-queue, calledqin.A pool of
workers: pool of the size of the number of cores. Eachworkeris doing the decompression of one chunk into one frame and the azimuthal integration of that frame. The integrated result is put into an output-queue, calledqout.2 queues:
qinandqout, the former is limited in size to prevent the filling-up of the memory, but large enough to feed the workers.
The gathering of the data is performed in the main thread but it could also be in a separated thread. Each piece of data is associated with its index in the dataset using the Item named-tuple.
Nota: I had a hard time to perform both reading and writing with HDF5 (even in different files). This is why the result is reconstructed in memory and the saving performed at the very end. Could be a bug in h5py.
[25]:
def reader(filename, h5path, queue, nbworkers):
"""Function reading the HDF5 file and enqueuing raw-chunks into the queue.
Used in a thread.
:param filename: name of the HDF5 file
:param h5path: path to the dataset within the HDF5 file
:param queue: queue where to put read chunks
:return: nothing, used in a thread."""
with h5py.File(filename, "r") as h:
ds = h["data"]
for i in range(ds.id.get_num_chunks()):
filter_mask, chunk = ds.id.read_direct_chunk(ds.id.get_chunk_info(i).chunk_offset)
if filter_mask==0:
while queue.full():
# slow down to prevent filling up memory
os.sched_yield()
queue.put(Item(i, chunk))
#kills all worker when done
for i in range(nbworkers):
while queue.full():
os.sched_yield()
queue.put(Item(-1, None))
[26]:
def worker(qin, qout):
"""Function representing one worker, used in a pool of worker.
:param qin: input queue, expects Item with index and compressed chunk
:param qout: output queue: puts item with index and integrated intensity
:return: nothing, used in a thread.
"""
while True:
item = qin.get()
index = item.index
if index<0:
qin.task_done()
qout.put(item)
return
frame = decompress_bslz4_chunk(item.data, dtype, shape)
qout.put(Item(index, engine.integrate_ng(frame, solidangle=omega).intensity))
qin.task_done()
[27]:
def build_pool(nbthreads, qin, qout):
"""Build a pool of threads with workers, and starts them"""
pool = [threading.Thread(target=worker, name=f"worker_{i:02d}", args=(qin, qout)) for i in range(nbthreads)]
for thread in pool:
thread.start()
return pool
def end_pool(pool):
"""Ends all threads from a pool by sending them a "kill-pill"""
for thread in pool:
qin.put(Item(-1, None))
#Small validation to check it works:
qin = Queue()
qout = Queue()
pool=build_pool(4, qin, qout)
end_pool(pool)
This cell contains all the processing for a serial reader + parallel (decompression+integration)
[28]:
%%timeit -o -r1 -n1 -q
# This is where all the magic is assembled
# Define the two queues
qin = Queue(maxsize=1000) # the size is used to slow-down the reading if needed
qout = Queue()
# Build the pool of workers
pool=build_pool(nbthreads, qin, qout)
# And start the reader who immediately starts filling the qin.
threading.Thread(target=reader, name="reader", args=(filename, "data", qin, len(pool))).start()
#The main thread gathers the data in the `qout`
result = numpy.zeros((nbframes, nbins), dtype=numpy.float32)
remaining = len(pool) #Number of remaining active workers
while remaining:
item = qout.get()
index = item.index
if index<0:
remaining -=1
else:
result[index] = item.data
qout.task_done()
# Finally ensure all tasks are done: this is redundant with remaining==0
qin.join()
qout.join()
[28]:
<TimeitResult : 8.31 s ± 0 ns per loop (mean ± std. dev. of 1 run, 1 loop each)>
[29]:
timing_parallel = _
print(f"Effective throughput: {nbframes/timing_parallel.best:.3f} fps and \nspeed-up versus the naive version is {timing_naive.best/timing_parallel.best:0.3f}x for a computer with {nbthreads} threads.")
Effective throughput: 492.691 fps and
speed-up versus the naive version is 25.762x for a computer with 64 threads.
One needs to replay the cell without the timeit to retrieve the results (timeit discards them!). Here is a version in a function:
[30]:
def integrate_hdf5(filename, dataset="/data",):
qin = Queue(maxsize=1000)
qout = Queue()
pool=build_pool(nbthreads, qin, qout)
threading.Thread(target=reader, name="reader", args=(filename, "data", qin, len(pool))).start()
#The main thread gathers the data in the `qout`
result = numpy.zeros((nbframes, nbins), dtype=numpy.float32)
remaining = len(pool) #Number of remaining active workers
while remaining:
item = qout.get()
index = item.index
if index<0: # kill-pill: worker has ended.
remaining -=1
else:
result[index] = item.data
qout.task_done()
return result
%time result = integrate_hdf5(filename)
with h5py.File("results.h5", "w") as results:
results.create_dataset("radial", data=res0.radial)
results.create_dataset("integrated", data=result)
CPU times: user 4min 12s, sys: 17.7 s, total: 4min 30s
Wall time: 8.67 s
Display some results
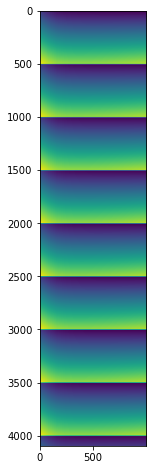
Since the input data were all synthetic and similar, no great science is expected from this… but one can ensure each frame differs slightly from the neighbors with a pattern of 500 frames.
[31]:
fig,ax = subplots(figsize=(8,8))
ax.imshow(result)
[31]:
<matplotlib.image.AxesImage at 0x14e66d675fa0>
Conclusion
Reading Bitshuffle-LZ4 data can be parallelized using multi-threading in Python.
The procedure is a bit tedious but not out of reach for a Python programmer: few threads and a couple of queues. This burden is worth when coupling decompression with azimuthal integration to reduce the amount of data stored in memory.
The performances obtained on a 64-core computer are close to what can be obtained from a GPU: ~500 fps The speed-up obtained with the procedure is 30x on a 64-core computer versus single threaded implementation, which demonstrates multithreading is worth the burden.
Thanks again to the French-CRG for the computer.
[32]:
print(f"Total processing time: {time.time()-start_time:.3f} s")
Total processing time: 332.644 s