Inpainting missing data
Missing data in an image can be an issue, especially when one wants to perform Fourier analysis. This tutorial explains how to fill-up missing pixels with values which looks “realistic” and introduce as little perturbation as possible for subsequent analysis. The user should keep the mask nearby and only consider the values of actual pixels and never the one inpainted.
This tutorial will use fully synthetic data to allow comparison between actual (syntetic) data with inpainted values.
The first part of the tutorial is about the generation of a challenging 2D diffraction image with realistic noise and to describe the metric used, then comes the actual tutorial on how to use the inpainting. Finally a benchmark is used based on the metric determined.
Creation of the image
A realistic challenging image should contain:
Bragg peak rings. We chose LaB6 as guinea-pig, with very sharp peaks, at the limit of the resolution of the detector
Some amorphous content
strong polarization effect
Poissonian noise
One image will be generated but then multiple ones with different noise to discriminate the effect of the noise from other effects.
[1]:
%matplotlib inline
# Used for documentation to inline plots into notebook
# %matplotlib widget
# uncomment the later for better UI
from matplotlib.pyplot import subplots
import numpy
[2]:
import pyFAI
print("Using pyFAI version: ", pyFAI.version)
from pyFAI.azimuthalIntegrator import AzimuthalIntegrator
from pyFAI.gui import jupyter
import pyFAI.test.utilstest
from pyFAI.calibrant import get_calibrant
import time
start_time = time.perf_counter()
Using pyFAI version: 2023.1.0-dev0
[3]:
detector = pyFAI.detector_factory("Pilatus2MCdTe")
mask = detector.mask.copy()
nomask = numpy.zeros_like(mask)
detector.mask=nomask
ai = AzimuthalIntegrator(detector=detector)
ai.setFit2D(200, 200, 200)
ai.wavelength = 3e-11
print(ai)
Detector Pilatus CdTe 2M PixelSize= 1.720e-04, 1.720e-04 m Detector Pilatus CdTe 2M PixelSize= 1.720e-04, 1.720e-04 m 172.0 172.0 None
Detector Pilatus CdTe 2M PixelSize= 1.720e-04, 1.720e-04 m
Wavelength= 3.000000e-11 m
SampleDetDist= 2.000000e-01 m PONI= 3.440000e-02, 3.440000e-02 m rot1=0.000000 rot2=0.000000 rot3=0.000000 rad
DirectBeamDist= 200.000 mm Center: x=200.000, y=200.000 pix Tilt= 0.000° tiltPlanRotation= 0.000° 𝛌= 0.300Å
[4]:
LaB6 = get_calibrant("LaB6")
LaB6.wavelength = ai.wavelength
print(LaB6)
r = ai.array_from_unit(unit="q_nm^-1")
decay_b = numpy.exp(-(r-50)**2/2000)
bragg = LaB6.fake_calibration_image(ai, Imax=1e4, W=1e-6) * ai.polarization(factor=1.0) * decay_b
decay_a = numpy.exp(-r/100)
amorphous = 1000*ai.polarization(factor=1.0)*ai.solidAngleArray() * decay_a
img_nomask = bragg + amorphous
#Not the same noise function for all images two images
img_nomask = numpy.random.poisson(img_nomask)
img_nomask2 = numpy.random.poisson(img_nomask)
img = numpy.random.poisson(img_nomask)
img[numpy.where(mask)] = -1
fig,ax = subplots(1,2, figsize=(10,5))
jupyter.display(img=img, label="With mask", ax=ax[0])
jupyter.display(img=img_nomask, label="Without mask", ax=ax[1])
LaB6 Calibrant with 640 reflections at wavelength 3e-11
[4]:
<AxesSubplot: title={'center': 'Without mask'}>
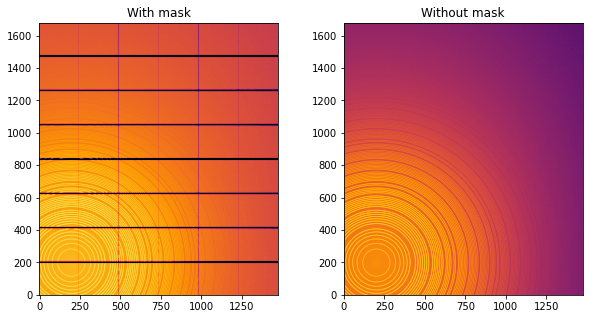
Note the aliassing effect on the displayed images.
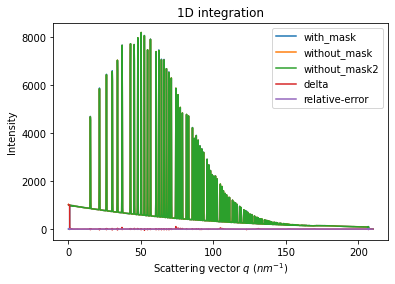
We will measure now the effect after 1D intergeration. We do not correct for polarization on purpose to highlight the defect one wishes to whipe out. We use a R-factor to describe the quality of the 1D-integrated signal.
[5]:
wo = ai.integrate1d(img_nomask, 2000, unit="q_nm^-1", method="splitpixel", radial_range=(0,210))
wo2 = ai.integrate1d(img_nomask2, 2000, unit="q_nm^-1", method="splitpixel", radial_range=(0,210))
wm = ai.integrate1d(img, 2000, unit="q_nm^-1", method="splitpixel", mask=mask, radial_range=(0,210))
ax = jupyter.plot1d(wm , label="with_mask")
ax.plot(*wo, label="without_mask")
ax.plot(*wo2, label="without_mask2")
ax.plot(wo.radial, wo.intensity-wm.intensity, label="delta")
ax.plot(wo.radial, wo.intensity-wo2.intensity, label="relative-error")
ax.legend()
print("Between masked and non masked image R= %s"%pyFAI.utils.mathutil.rwp(wm,wo))
print("Between two different non-masked images R'= %s"%pyFAI.utils.mathutil.rwp(wo2,wo))
Between masked and non masked image R= 5.6770861389915614
Between two different non-masked images R'= 0.4932559811828495
[6]:
# Effect of the noise on the delta image
fig, ax = subplots()
jupyter.display(img=img_nomask-img_nomask2, label="Delta due to noise", ax=ax)
ax.figure.colorbar(ax.images[0])
[6]:
<matplotlib.colorbar.Colorbar at 0x7f36828e9280>
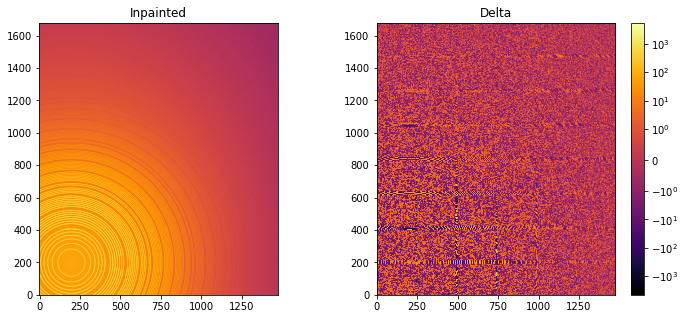
Inpainting
This part describes how to paint the missing pixels for having a “natural-looking image”. The delta image contains the difference with the original image
[7]:
#Inpainting:
inpainted = ai.inpainting(img, mask=mask, poissonian=True)
fig, ax = subplots(1, 2, figsize=(12,5))
jupyter.display(img=inpainted, label="Inpainted", ax=ax[0])
jupyter.display(img=img_nomask-inpainted, label="Delta", ax=ax[1])
ax[1].figure.colorbar(ax[1].images[0])
[7]:
<matplotlib.colorbar.Colorbar at 0x7f36826accd0>
[8]:
# Comparison of the inpained image with the original one:
wm = ai.integrate1d(inpainted, 2000, unit="q_nm^-1", method="splitpixel", radial_range=(0,210))
wo = ai.integrate1d(img_nomask, 2000, unit="q_nm^-1", method="splitpixel", radial_range=(0,210))
ax = jupyter.plot1d(wm , label="inpainted")
ax.plot(*wo, label="without_mask")
ax.plot(wo.radial, wo.intensity-wm.intensity, label="delta")
ax.legend()
print("R= %s"%pyFAI.utils.mathutil.rwp(wm,wo))
R= 1.2791830680558827
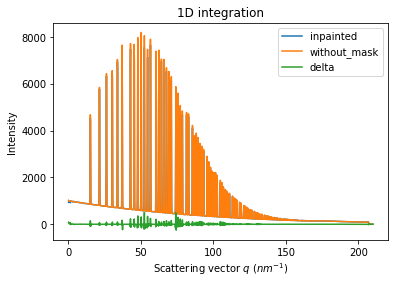
One can see by zooming in that the main effect on inpainting is a broadening of the signal in the inpainted region. This could (partially) be adressed by increasing the number of radial bins used in the inpainting.
Benchmarking and optimization of the parameters
The parameter set depends on the detector, the experiment geometry and the type of signal on the detector. Finer detail require finer slicing.
[9]:
#Basic benchmarking of execution time for default options:
%timeit inpainted = ai.inpainting(img, mask=mask)
1.77 s ± 11.1 ms per loop (mean ± std. dev. of 7 runs, 1 loop each)
[10]:
wo = ai.integrate1d(img_nomask, 2000, unit="q_nm^-1", method="splitpixel", radial_range=(0,210))
for m in (("no", "histogram", "cython"), ("bbox", "histogram","cython")):
for k in (512, 1024, 2048, 4096):
ai.reset()
for i in (0, 1, 2, 4, 8):
inpainted = ai.inpainting(img, mask=mask, poissonian=True, method=m, npt_rad=k, grow_mask=i)
wm = ai.integrate1d(inpainted, 2000, unit="q_nm^-1", method="splitpixel", radial_range=(0,210))
print(f"method: {m} npt_rad={k} grow={i}; R= {pyFAI.utils.mathutil.rwp(wm,wo)}")
method: ('no', 'histogram', 'cython') npt_rad=512 grow=0; R= 3.8767938689475305
method: ('no', 'histogram', 'cython') npt_rad=512 grow=1; R= 2.966655396652616
method: ('no', 'histogram', 'cython') npt_rad=512 grow=2; R= 2.691669300640641
method: ('no', 'histogram', 'cython') npt_rad=512 grow=4; R= 2.5906399838261978
method: ('no', 'histogram', 'cython') npt_rad=512 grow=8; R= 2.525984580085641
method: ('no', 'histogram', 'cython') npt_rad=1024 grow=0; R= 2.7763037272589175
method: ('no', 'histogram', 'cython') npt_rad=1024 grow=1; R= 1.4432439988102326
method: ('no', 'histogram', 'cython') npt_rad=1024 grow=2; R= 1.3537089504081086
method: ('no', 'histogram', 'cython') npt_rad=1024 grow=4; R= 1.2951771458333021
method: ('no', 'histogram', 'cython') npt_rad=1024 grow=8; R= 1.1665124687886776
method: ('no', 'histogram', 'cython') npt_rad=2048 grow=0; R= 2.834675478220375
method: ('no', 'histogram', 'cython') npt_rad=2048 grow=1; R= 1.2799642176276504
method: ('no', 'histogram', 'cython') npt_rad=2048 grow=2; R= 1.1662380752800603
method: ('no', 'histogram', 'cython') npt_rad=2048 grow=4; R= 1.036650606780755
method: ('no', 'histogram', 'cython') npt_rad=2048 grow=8; R= 0.8501408503671106
method: ('no', 'histogram', 'cython') npt_rad=4096 grow=0; R= 2.7083330585184147
method: ('no', 'histogram', 'cython') npt_rad=4096 grow=1; R= 1.241410949409031
method: ('no', 'histogram', 'cython') npt_rad=4096 grow=2; R= 1.2158663175139999
method: ('no', 'histogram', 'cython') npt_rad=4096 grow=4; R= 1.1601341894672716
method: ('no', 'histogram', 'cython') npt_rad=4096 grow=8; R= 1.0196521572380268
method: ('bbox', 'histogram', 'cython') npt_rad=512 grow=0; R= 3.165256893124079
method: ('bbox', 'histogram', 'cython') npt_rad=512 grow=1; R= 2.9118578039114253
method: ('bbox', 'histogram', 'cython') npt_rad=512 grow=2; R= 2.7168848728531443
method: ('bbox', 'histogram', 'cython') npt_rad=512 grow=4; R= 2.632899442981269
method: ('bbox', 'histogram', 'cython') npt_rad=512 grow=8; R= 2.5425631980313317
method: ('bbox', 'histogram', 'cython') npt_rad=1024 grow=0; R= 1.6935840361345331
method: ('bbox', 'histogram', 'cython') npt_rad=1024 grow=1; R= 1.3412097896474042
method: ('bbox', 'histogram', 'cython') npt_rad=1024 grow=2; R= 1.33411747527533
method: ('bbox', 'histogram', 'cython') npt_rad=1024 grow=4; R= 1.2915463751417635
method: ('bbox', 'histogram', 'cython') npt_rad=1024 grow=8; R= 1.2772322098686615
method: ('bbox', 'histogram', 'cython') npt_rad=2048 grow=0; R= 0.9118272803820315
method: ('bbox', 'histogram', 'cython') npt_rad=2048 grow=1; R= 0.6745118073480101
method: ('bbox', 'histogram', 'cython') npt_rad=2048 grow=2; R= 0.6600472782370277
method: ('bbox', 'histogram', 'cython') npt_rad=2048 grow=4; R= 0.6580426274859333
method: ('bbox', 'histogram', 'cython') npt_rad=2048 grow=8; R= 0.6541503711200992
method: ('bbox', 'histogram', 'cython') npt_rad=4096 grow=0; R= 0.5933174014934481
method: ('bbox', 'histogram', 'cython') npt_rad=4096 grow=1; R= 0.45103699613613096
method: ('bbox', 'histogram', 'cython') npt_rad=4096 grow=2; R= 0.46199100406404975
method: ('bbox', 'histogram', 'cython') npt_rad=4096 grow=4; R= 0.4552640962924382
method: ('bbox', 'histogram', 'cython') npt_rad=4096 grow=8; R= 0.4585132787535523
[11]:
#Inpainting, best solution found:
ai.reset()
%time inpainted = ai.inpainting(img, mask=mask, poissonian=True, method=("pseudo", "csr", "cython"), npt_rad=4096, grow_mask=1)
fig, ax = subplots(1, 2, figsize=(12, 5))
jupyter.display(img=inpainted, label="Inpainted", ax=ax[0])
jupyter.display(img=img_nomask-inpainted, label="Delta", ax=ax[1])
ax[1].figure.colorbar(ax[1].images[0])
pass
CPU times: user 2.88 s, sys: 115 ms, total: 2.99 s
Wall time: 2.62 s
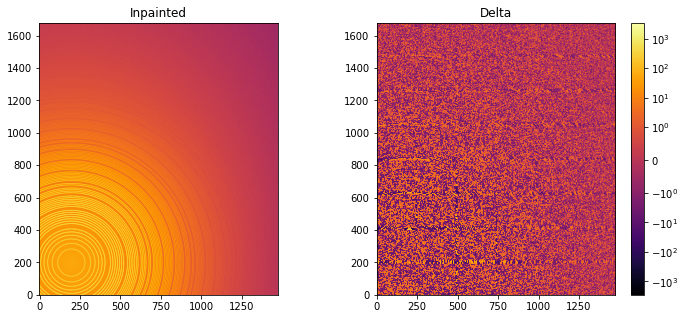
[12]:
# Comparison of the inpained image with the original one:
wm = ai.integrate1d(inpainted, 2000, unit="q_nm^-1", method="splitpixel", radial_range=(0,210))
wo = ai.integrate1d(img_nomask, 2000, unit="q_nm^-1", method="splitpixel", radial_range=(0,210))
ax = jupyter.plot1d(wm , label="inpainted")
ax.plot(*wo, label="without_mask")
ax.plot(wo.radial, wo.intensity-wm.intensity, label="delta")
ax.legend()
print("R= %s"%pyFAI.utils.mathutil.rwp(wm,wo))
R= 1.715456247623005
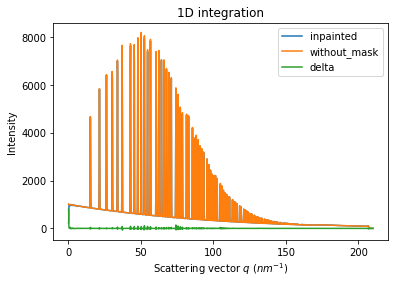
Conclusion
Inpainting is one of the only solution to fill up the gaps in detector when Fourier analysis is needed. This tutorial explains basically how this is possible using the pyFAI library and how to optimize the parameter set for inpainting. The result may greatly vary with detector position and tilt and the kind of signal (amorphous or more spotty).
[13]:
print(f"Execution time: {time.perf_counter()-start_time:.3f} s")
Execution time: 68.552 s