Distortion of Eiger2 CdTe detector from ID11
The detector’s distortion is characterized by a Tungsten plate with a grid pattern of holes provided by Gavin Vaughan. The calibration experiment has been performed by Marie Ruat with a conventional source. Those files are not available for share, please get in contact with Marie for the experimental details.
Preprocessing
Data were acquired with and without the grid on from of the detector. 100 frames were recorded in each case withthe same exposure time. The first step is to filter out outliers using a pixel-wise median filter on the stack.
Note: a faily recent version of FabIO is needed to read those HDF5 files produced by LImA. This notebook uses features available only in version 0.21 of pyFAI (development version for now)
[1]:
%matplotlib inline
#For documentation purpose, `inline` is used to enforce the storage of the image in the notebook
# %matplotlib widget
import time
import os
start_time = time.perf_counter()
#load many libraries ...
from matplotlib.pyplot import subplots
import matplotlib.colors as colors
import numpy
import pyFAI
from collections import namedtuple
from scipy.ndimage import convolve, binary_dilation, label, distance_transform_edt
from scipy.spatial import distance_matrix
from pyFAI.ext.watershed import InverseWatershed
from pyFAI.ext.bilinear import Bilinear
from pyFAI.utils.grid import Kabsch #Needs pyFAI 0.21!
[2]:
#Get the grid/flat data and filter them
!wget http://www.silx.org/pub/pyFAI/detector_calibration/Eiger2-ID11/W200um_40kVp_5mA_T4_E8_FF_noretrigger_0000.h5
!wget http://www.silx.org/pub/pyFAI/detector_calibration/Eiger2-ID11/W200um_40kVp_5mA_T4_E8_GRID_noretrigger_0000.h5
!pyFAI-average -m median W200um_40kVp_5mA_T4_E8_FF_noretrigger_0000.h5 -F numpy -o flat.npy
!pyFAI-average -m median W200um_40kVp_5mA_T4_E8_GRID_noretrigger_0000.h5 -F numpy -o grid.npy
--2024-09-12 11:56:23-- http://www.silx.org/pub/pyFAI/detector_calibration/Eiger2-ID11/W200um_40kVp_5mA_T4_E8_FF_noretrigger_0000.h5
Resolving www.silx.org (www.silx.org)... 195.154.237.27
Connecting to www.silx.org (www.silx.org)|195.154.237.27|:80... connected.
HTTP request sent, awaiting response... 200 OK
Length: 758913619 (724M)
Saving to: ‘W200um_40kVp_5mA_T4_E8_FF_noretrigger_0000.h5.1’
W200um_40kVp_5mA_T4 100%[===================>] 723.76M 56.0MB/s in 12s
2024-09-12 11:56:35 (61.7 MB/s) - ‘W200um_40kVp_5mA_T4_E8_FF_noretrigger_0000.h5.1’ saved [758913619/758913619]
--2024-09-12 11:56:35-- http://www.silx.org/pub/pyFAI/detector_calibration/Eiger2-ID11/W200um_40kVp_5mA_T4_E8_GRID_noretrigger_0000.h5
Resolving www.silx.org (www.silx.org)... 195.154.237.27
Connecting to www.silx.org (www.silx.org)|195.154.237.27|:80... connected.
HTTP request sent, awaiting response... 200 OK
Length: 484110560 (462M)
Saving to: ‘W200um_40kVp_5mA_T4_E8_GRID_noretrigger_0000.h5.1’
W200um_40kVp_5mA_T4 100%[===================>] 461.68M 87.7MB/s in 6.8s
2024-09-12 11:56:42 (67.9 MB/s) - ‘W200um_40kVp_5mA_T4_E8_GRID_noretrigger_0000.h5.1’ saved [484110560/484110560]
INFO:numexpr.utils:NumExpr defaulting to 16 threads.
Median reduction finished
INFO:numexpr.utils:NumExpr defaulting to 16 threads.
Median reduction finished
[3]:
# A couple of constants and compound dtypes ...
dt = numpy.dtype([('y', numpy.float64),
('x', numpy.float64),
('i', numpy.int64),
])
mpl = {"cmap":"viridis",
"interpolation":"nearest"}
print("Using pyFAI verison: ", pyFAI.version)
Using pyFAI verison: 2024.9.0-dev0
[4]:
flat = numpy.load("flat.npy")
grid = numpy.load("grid.npy")
fig, ax = subplots(figsize=(8,8))
ax.imshow(grid/flat, **mpl)
ax.set_title("Raw grid (normalized)")
pass
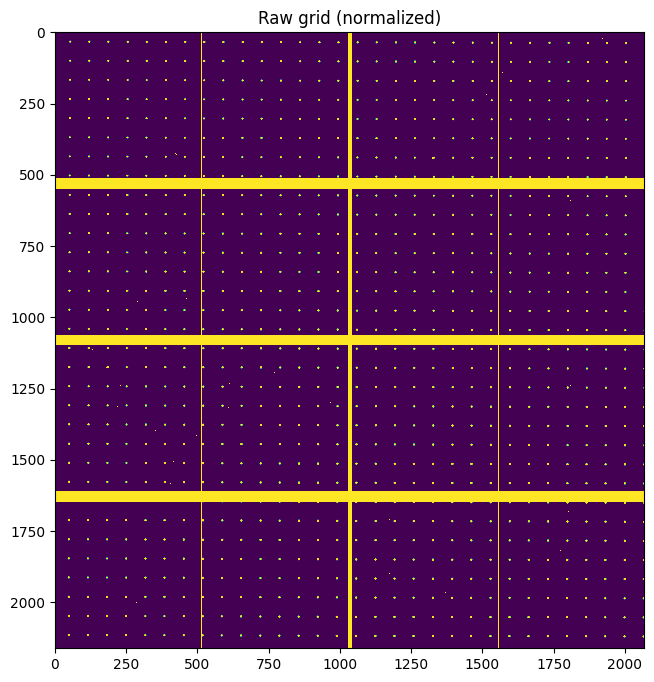
Define the right mask
As we want to measure the position of the grid with a sub-pixel precision, it is of crutial important to discard all pixels wich have been interpolated.
The Eiger2 4M is built of 8 modules 500 kpixels, each of them consists of the assemble of 8 chips of 256x256 pixel each. Some pixels are systematically masked out as they are known to be noisy. Some pixels are also missing at the junction of the sub-modules. Finally the CdTe sensors is made of single crystals of the semi-conductor which cover 512x512 pixels. Hence one sensor covers half a module or 4 chips.
This is best demonstrated by the pixel-wise standard deviation along a stack of images like the one acquired for the flatfield.
A Poissonian detector should have a variance equal to the average signal. Thus plotting the standard deviation squared over the median highlights: * Noisy pixels which should be discarded for quantitative analysis std²>>median * Interpolated pixels which have only half/quater of the expected noise (std²<<median).
The detector has also an internal map of invalid pixel which are set to the maximum value of the range.
[5]:
!pyFAI-average -m std W200um_40kVp_5mA_T4_E8_FF_noretrigger_0000.h5 -F numpy -o flat_std.npy
INFO:numexpr.utils:NumExpr defaulting to 16 threads.
Std reduction finished
[6]:
std = numpy.load("flat_std.npy")
fig, ax = subplots(figsize=(8,8))
ax.imshow((std**2/flat).clip(0,2), **mpl)
ax.set_title("Poissonianness map of the detctor (std²/median ~ 1)")
pass
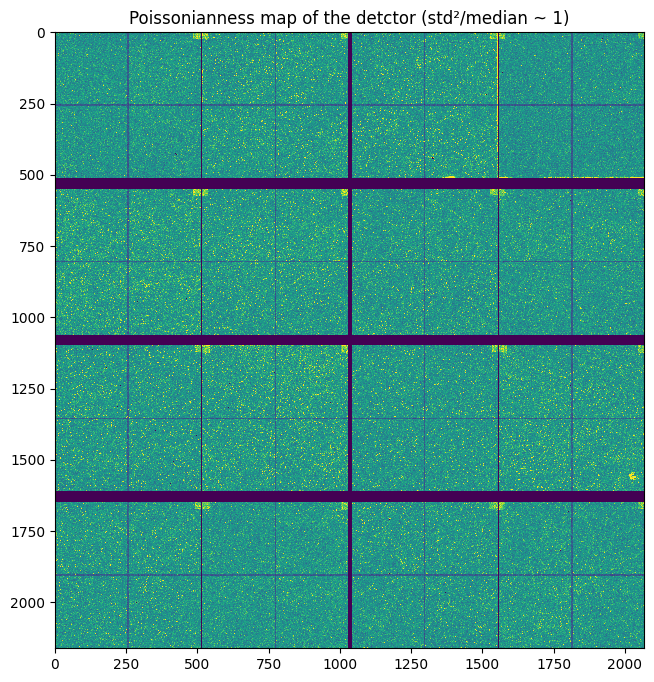
[7]:
fig, ax = subplots()
ax.hist((std**2/flat).ravel(), 100, range=(0,2))
ax.set_title("Histogram of std²/median values")
pass
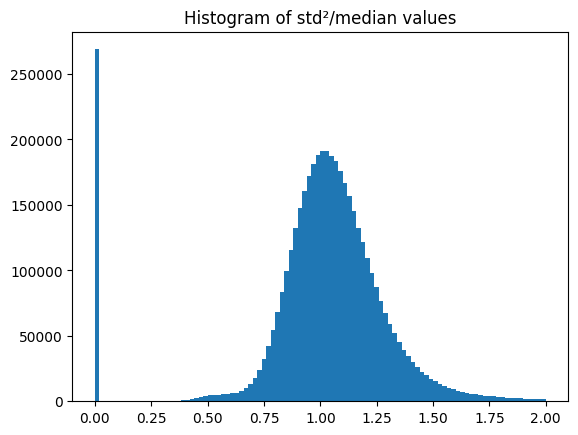
This test of Poissonian-ness is not enough to discriminate between interpolated pixels and non interpolated ones. One needs to build the mask by other methods.
[8]:
# This is the default detector as definied in pyFAI according to the specification provided by Dectris:
eiger2 = pyFAI.detector_factory("Eiger2CdTe_4M")
width = eiger2.shape[1]
module_size = eiger2.MODULE_SIZE
module_gap = eiger2.MODULE_GAP
submodule_size = (256,256)
[9]:
#Calculate the default mask
mask = eiger2.calc_mask()
# Mask out the interpolated pixels along X
for j in [256, 772]:
for i in range(j, eiger2.max_shape[1],
eiger2.module_size[1] + eiger2.MODULE_GAP[1]):
mask[:,i-2:i + 2] = 1
# Mask out the interpolated pixels along Y
for i in range(256, eiger2.max_shape[0],
eiger2.module_size[0] + eiger2.MODULE_GAP[0]):
mask[i-2:i + 2, :] = 1
# mask out the border pixels:
mask[0] = 1
mask[-1] = 1
mask[:, 0] = 1
mask[:, -1] = 1
# Finally mask out invalid/miss-behaving pixels known from the detector
mask[ flat>(flat.max()*0.99) ] = 1
[10]:
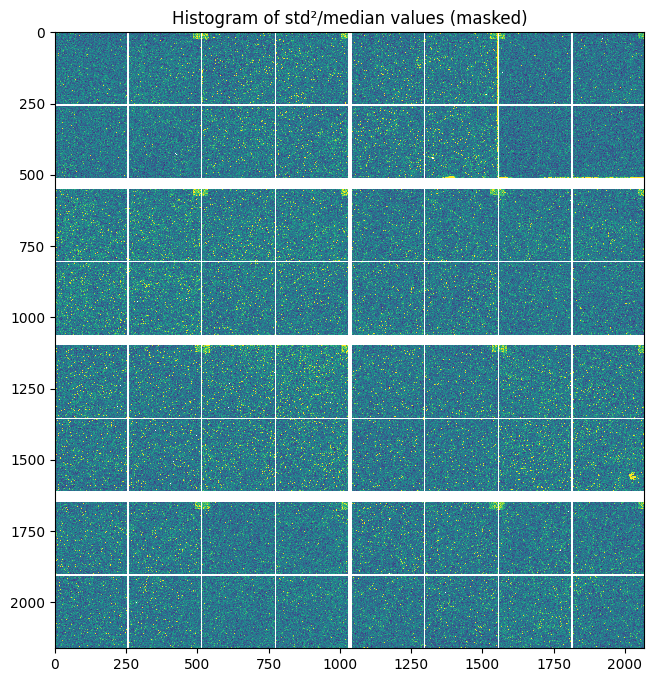
pois = (std**2/flat).clip(0,2)
pois[numpy.where(mask)] = numpy.nan
fig, ax = subplots(figsize=(8,8))
ax.imshow(pois, **mpl)
ax.set_title("Histogram of std²/median values (masked)")
pass
[11]:
normalized = grid/flat
normalized[numpy.where(mask)] = numpy.nan
fig, ax = subplots(figsize=(8,8))
ax.imshow(normalized, **mpl)
ax.set_ylim(1100,1400)
ax.set_xlim(1000,1300)
ax.set_title("Zoom on one chip")
pass
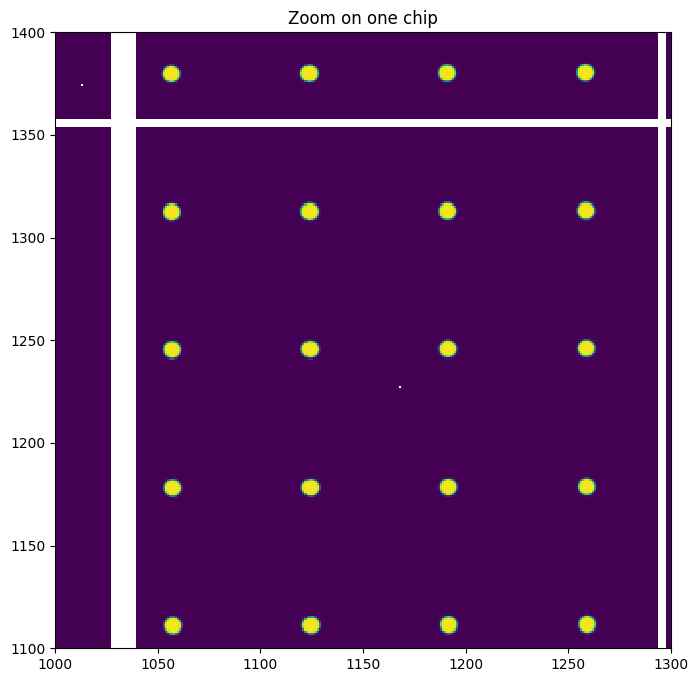
We can see we have between 8 and 16 grid spots per sub-module. This is enough as 3 are needed to localize precisely the position of the chip.
Grid spot position measurement.
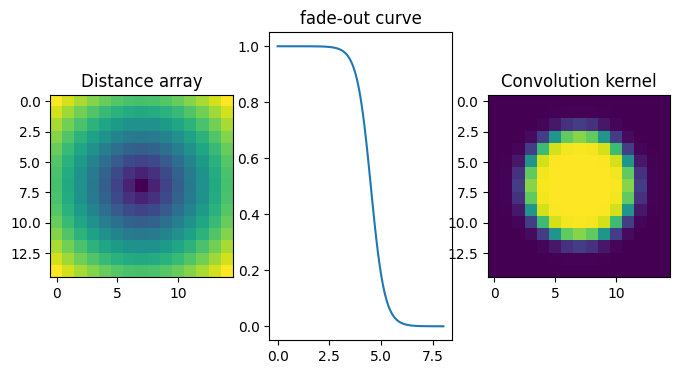
Let’s measure the position of the grid spots precisely. For this we perform a convolution with a kernel which looks like the spot itself. By zooming onto one spot, it is roughly 10 pixels wide, the kernel needs to be of odd size. The fade-out function is tuned to set precisely the spot diameter.
The masked values have been set to NaN, this ensures any spot close to a masked region get discarded automatically.
[12]:
#Definition of the convolution kernel
ksize = 15
y,x = numpy.ogrid[-(ksize-1)//2:ksize//2+1,-(ksize-1)//2:ksize//2+1]
d = numpy.sqrt(y*y+x*x)
#Fade out curve definition
fadeout = lambda x: 1/(1+numpy.exp(3*(x-4.5)))
kernel = fadeout(d)
mini=kernel.sum()
print("Integral of the kernel: ", mini)
fig,ax = subplots(1,3, figsize=(8,4))
ax[0].imshow(d)
ax[0].set_title("Distance array")
ax[1].plot(numpy.linspace(0,8,100),fadeout(numpy.linspace(0,8,100)))
ax[1].set_title("fade-out curve")
ax[2].imshow(kernel)
ax[2].set_title("Convolution kernel")
pass
Integral of the kernel: 64.79908175810988
[13]:
smooth = convolve(normalized, kernel, mode="constant", cval=0)/mini
fig,ax = subplots(1,2, figsize=(8,4))
ax[0].imshow(normalized)
ax[0].set_ylim(1100,1400)
ax[0].set_xlim(1000,1300)
ax[1].imshow(smooth)
ax[1].set_ylim(1100,1400)
ax[1].set_xlim(1000,1300)
ax[0].set_title("Grid (zoomed)")
ax[1].set_title("Smoothed grid")
pass
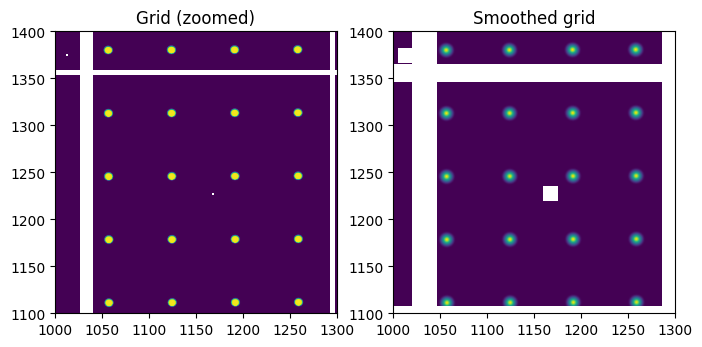
[14]:
# Calculate a mask with all pixels close to any gap is discared
#big_mask = numpy.isnan(smooth)
big_mask = binary_dilation(numpy.isnan(smooth), iterations=ksize//2+2) #even a bit larger
#big_mask = binary_dilation(mask, iterations=ksize) #Extremely conservative !
Peak position measurement
The center of spot is now easily measured by segmenting out the image
[15]:
iw = InverseWatershed(smooth)
iw.init()
iw.merge_singleton()
all_regions = set(iw.regions.values())
regions = [i for i in all_regions if i.size>mini]
print("Number of region segmented: %s"%len(all_regions))
print("Number of large enough regions : %s"%len(regions))
Number of region segmented: 837883
Number of large enough regions : 5968
[16]:
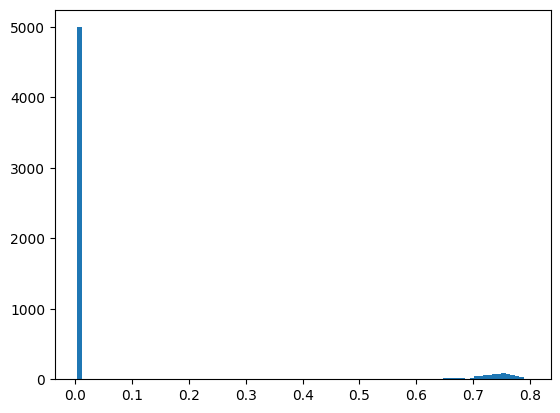
# Histogram of peak height:
s = numpy.array([i.maxi for i in regions])
fig, ax = subplots()
ax.hist(s, 100)
pass
[17]:
#Sieve-out for peak intensity
int_mini = 0.5
peaks = [(i.index//width, i.index%width) for i in regions if (i.maxi)>int_mini and
not big_mask[(i.index//width, i.index%width)]]
print("Number of remaining peaks with I>%s: %s"%(int_mini, len(peaks)))
peaks_raw = numpy.array(peaks)
Number of remaining peaks with I>0.5: 694
About 800 spots were found as valid out of a maximum of 1024 (64 chips with 16 spots per chip)
Those spot positions are interpolated using a second order taylor expansion in the region around the maximum value of the smoothed image.
[18]:
#Use a bilinear interpolator to localize/refine the maxima
bl = Bilinear(smooth)
ref_peaks = [bl.local_maxi(p) for p in peaks]
[19]:
#Overlay raw peak coordinate and refined peak positions
fig, ax = subplots(figsize=(8,8))
ax.imshow(normalized, **mpl)
peaks_ref = numpy.array(ref_peaks)
ax.plot(peaks_raw[:,1], peaks_raw[:, 0], ".r")
ax.plot(peaks_ref[:,1],peaks_ref[:, 0], ".b")
ax.set_title("Extracted peak position (red: raw, blue: refined)")
print("Refined peak coordinate:", ref_peaks[:10], "...")
Refined peak coordinate: [(167.233992934227, 52.1488603502512), (167.40148302912712, 119.33040842413902), (167.60313618183136, 186.51580595970154), (168.13941171765327, 321.02641019411385), (168.32840502262115, 388.20942007005215), (168.4771248102188, 455.6033400297165), (169.1162062138319, 589.783746868372), (169.31707295775414, 656.974004779011), (169.57376378774643, 724.1835104823112), (169.68481066823006, 791.394011169672)] ...
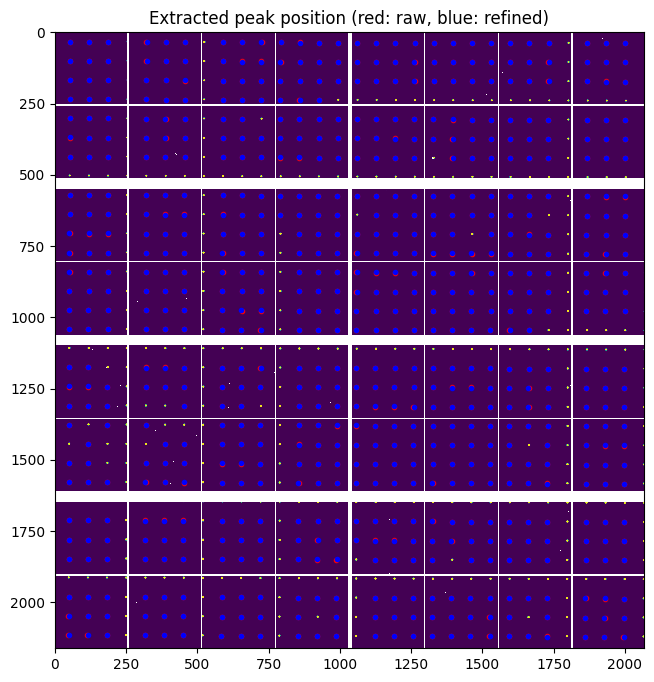
At this stage we have about 800 peaks (with sub-pixel precision) which are visually distributed on all modules and on all chips. We could have expected 16*64=1024 hence most of the spots were properly located.
Let’s assign each peak to a module identifier. This allows to print out the number of peaks per module:
[20]:
#Module identification
mid, cnt = label(numpy.isfinite(normalized), structure=numpy.ones((3,3), dtype=int))
print(cnt, "chips have been labeled")
64 chips have been labeled
[21]:
# Fill the gaps in module identification array
#From http://stackoverflow.com/questions/3662361/fill-in-missing-values-with-nearest-neighbour-in-python-numpy-masked-arrays
def fill(data, invalid=None):
"""
Replace the value of invalid 'data' cells (indicated by 'invalid')
by the value of the nearest valid data cell
Input:
data: numpy array of any dimension
invalid: a binary array of same shape as 'data'. True cells set where data
value should be replaced.
If None (default), use: invalid = np.isnan(data)
Output:
Return a filled array.
"""
if invalid is None:
invalid = numpy.isnan(data)
ind = distance_transform_edt(invalid, return_distances=False, return_indices=True)
return data[tuple(ind)]
filled_mid = fill(mid, invalid=mid==0)
[22]:
fig,ax = subplots(1, 2, figsize=(10,5))
ax[0].imshow(mid, **mpl)
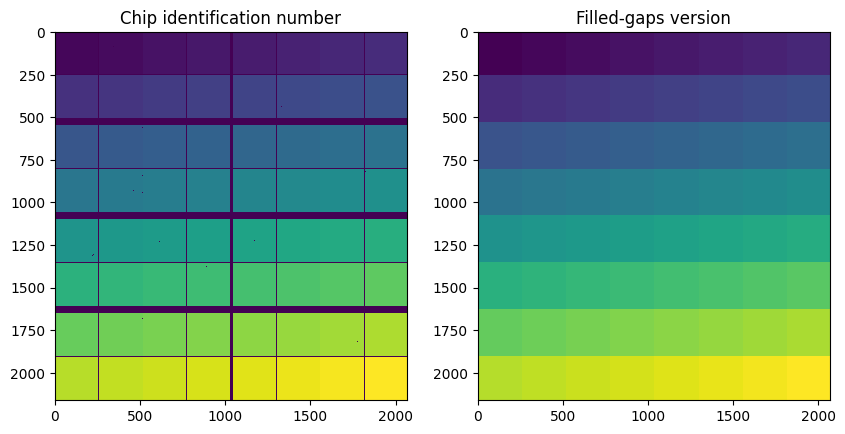
ax[0].set_title("Chip identification number")
ax[1].imshow(filled_mid, **mpl)
ax[1].set_title("Filled-gaps version")
pass
[23]:
yxi = numpy.array([i+(mid[round(i[0]),round(i[1])],)
for i in ref_peaks], dtype=dt)
print("Number of keypoint per chip:")
for i in range(1, cnt+1):
print(f"Chip id: {i:2d} \t Number of spots: {(yxi[:]['i'] == i).sum():2d}")
Number of keypoint per chip:
Chip id: 1 Number of spots: 12
Chip id: 2 Number of spots: 12
Chip id: 3 Number of spots: 12
Chip id: 4 Number of spots: 15
Chip id: 5 Number of spots: 12
Chip id: 6 Number of spots: 12
Chip id: 7 Number of spots: 9
Chip id: 8 Number of spots: 9
Chip id: 9 Number of spots: 9
Chip id: 10 Number of spots: 9
Chip id: 11 Number of spots: 8
Chip id: 12 Number of spots: 12
Chip id: 13 Number of spots: 12
Chip id: 14 Number of spots: 11
Chip id: 15 Number of spots: 9
Chip id: 16 Number of spots: 9
Chip id: 17 Number of spots: 12
Chip id: 18 Number of spots: 12
Chip id: 19 Number of spots: 12
Chip id: 20 Number of spots: 14
Chip id: 21 Number of spots: 15
Chip id: 22 Number of spots: 15
Chip id: 23 Number of spots: 11
Chip id: 24 Number of spots: 12
Chip id: 25 Number of spots: 12
Chip id: 26 Number of spots: 12
Chip id: 27 Number of spots: 12
Chip id: 28 Number of spots: 12
Chip id: 29 Number of spots: 16
Chip id: 30 Number of spots: 16
Chip id: 31 Number of spots: 11
Chip id: 32 Number of spots: 9
Chip id: 33 Number of spots: 8
Chip id: 34 Number of spots: 7
Chip id: 35 Number of spots: 8
Chip id: 36 Number of spots: 9
Chip id: 37 Number of spots: 12
Chip id: 38 Number of spots: 12
Chip id: 39 Number of spots: 9
Chip id: 40 Number of spots: 9
Chip id: 41 Number of spots: 8
Chip id: 42 Number of spots: 9
Chip id: 43 Number of spots: 12
Chip id: 44 Number of spots: 12
Chip id: 45 Number of spots: 16
Chip id: 46 Number of spots: 16
Chip id: 47 Number of spots: 11
Chip id: 48 Number of spots: 12
Chip id: 49 Number of spots: 9
Chip id: 50 Number of spots: 9
Chip id: 51 Number of spots: 9
Chip id: 52 Number of spots: 9
Chip id: 53 Number of spots: 11
Chip id: 54 Number of spots: 11
Chip id: 55 Number of spots: 9
Chip id: 56 Number of spots: 9
Chip id: 57 Number of spots: 9
Chip id: 58 Number of spots: 9
Chip id: 59 Number of spots: 9
Chip id: 60 Number of spots: 8
Chip id: 61 Number of spots: 9
Chip id: 62 Number of spots: 12
Chip id: 63 Number of spots: 8
Chip id: 64 Number of spots: 9
Grid assignment
The calibration is performed using a regular grid, the idea is to assign to each peak of coordinates (x,y) the integer value (X, Y) which correspond to the grid corrdinate system.
The first step is to measure the grid pitch which correspond to the distance (in pixels) from one peak to the next. This is easily obtained from a pair-wise distribution function.
[24]:
# pairwise distance calculation using scipy.spatial.distance_matrix
dist = distance_matrix(peaks_ref, peaks_ref)
fig, ax = subplots()
ax.hist(dist.ravel(), 200, range=(0,200))
ax.set_title("Pair-wise distribution function")
ax.set_xlabel("Distance (pixel)")
ax.set_ylabel("Occurances")
pass
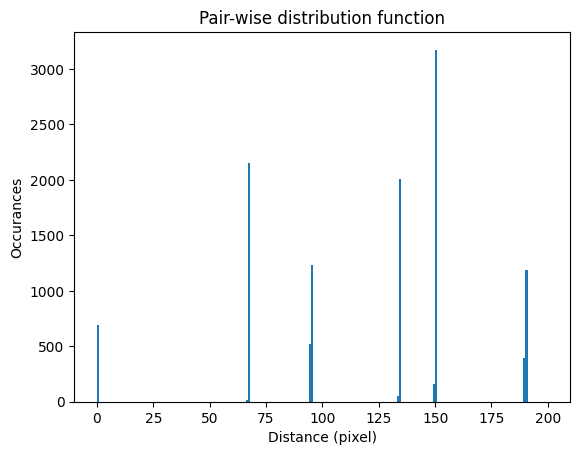
The histogram of the pair-distribution function has a first peak at 0 and the second peak between 66 and 67. The value of the step size is taken as the average of this second peak in the histogram as it correspond to the first neighbour distance.
Two other parameters correspond to the offset, in pixels, for the grid index (X,Y) = (0,0). The easiest is to measure the smallest x and y for the first chip.
The grid looks pretty well aligned with the detector, so we will not take into account the rotation of the grid with the detector.
[25]:
#from pair-wise distribution histogram
valid_pairs = dist[numpy.logical_and(60<dist, dist<70)]
step = valid_pairs.mean()
print("Average step size", step, "±", valid_pairs.std(), " pixels, condidering ", valid_pairs.size, "paires")
Average step size 67.20435086643545 ± 0.0739548221714359 pixels, condidering 2170 paires
[26]:
#Refinement of the step size when considering only intra-chip distances.
intra_distances = []
inter_distances = []
extra = []
for i in range(1, cnt+1):
locale = yxi[yxi[:]["i"] == i]
xy = tmp = numpy.vstack((locale["x"], locale["y"])).T
ldist = distance_matrix(tmp, tmp).ravel()
intra_distances.append(ldist)
if extra:
inter_distances.append(distance_matrix(tmp, numpy.concatenate(extra)).ravel())
extra.append(tmp)
valid_pairs = numpy.concatenate([ i[numpy.logical_and(60<i, i<70)] for i in intra_distances])
step = valid_pairs.mean()
print("Average step size", step, "±", valid_pairs.std(), " pixels, condidering ", valid_pairs.size, "paires")
Average step size 67.20456994710561 ± 0.06025153104484155 pixels, condidering 1888 paires
It is interesting to note the standard deviation (0.06 pixel) corresponds to the precision of our measurement, approximately 5µm. This is mostly related to the procedure for the grid manufacturing.
Any tweaking when defining the kernel prior to the convolution should be checked against this error.
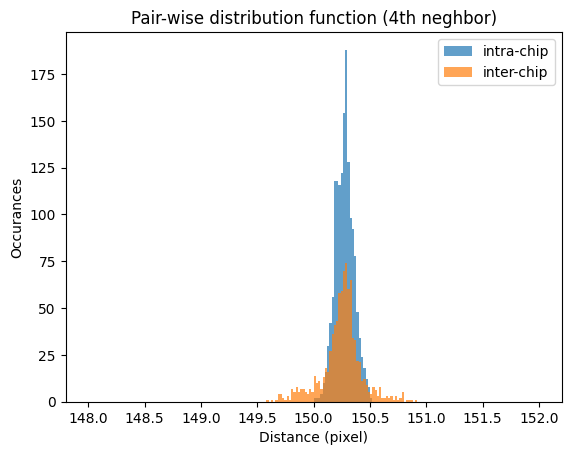
Since first neighbors are often on the same chip, so they are not representative for the distortion of the detector. Let’s rather observe the \(4^{th}\) neighbor which is at 150 pixel away and correspond a move similar to the “knight move” at the chess play: 2 in one direction and on in the other. This allows not only to probe the neighboring chips in the horizontal and vertical direction but also in the diagonal. The distance for this move is \(step*\sqrt{2^2+1^2}\).
[27]:
#4th neighbor: 150 pixels away
intra_pairs = numpy.concatenate([ i[numpy.logical_and(140<i, i<160)] for i in intra_distances])
inter_pairs = numpy.concatenate([ i[numpy.logical_and(140<i, i<160)] for i in inter_distances])
fig, ax = subplots()
ax.hist(intra_pairs, 200, range=(148, 152), alpha=0.7, label="intra-chip")
ax.hist(inter_pairs, 200, range=(148, 152), alpha=0.7, label="inter-chip")
ax.set_title("Pair-wise distribution function (4th neghbor)")
ax.set_xlabel("Distance (pixel)")
ax.set_ylabel("Occurances")
ax.legend()
print(f"Intra-chip average 4th neighbor distance {intra_pairs.mean():.3f}±{intra_pairs.std():.3f} pixels, condidering {intra_pairs.size} paires")
print(f"Inter-chip average 4th neighbor distance {inter_pairs.mean():.3f}±{inter_pairs.std():.3f} pixels, condidering {inter_pairs.size} paires")
Intra-chip average 4th neighbor distance 150.275±0.080 pixels, condidering 1522 paires
Inter-chip average 4th neighbor distance 150.249±0.182 pixels, condidering 904 paires
[28]:
#work with the first module and fit the peak positions
first = yxi[yxi[:]["i"] == 1]
y_min = first[:]["y"].min()
x_min = first[:]["x"].min()
print("offset for the first spot: ", x_min, y_min)
offset for the first spot: 52.00244328239933 32.73367205262184
The grid looks very well aligned with the axes which makes this step easier but nothing garanties it is perfect, so the rotation of the grid has to be measured as well. We will use Kabsch’s algoritm for this: https://en.wikipedia.org/wiki/Kabsch_algorithm
[29]:
reference_1 = numpy.empty((first.size, 2))
measured_1 = numpy.empty((first.size, 2))
measured_1[:, 0] = first[:]["x"]
measured_1[:, 1] = first[:]["y"]
reference_1[:, 0] = numpy.round((first[:]["x"]-x_min)/step)*step+x_min
reference_1[:, 1] = numpy.round((first[:]["y"]-y_min)/step)*step+y_min
%time Kabsch(reference_1, measured_1)
CPU times: user 616 μs, sys: 32 μs, total: 648 μs
Wall time: 598 μs
[29]:
Rigid transformation of angle -0.167° and translation [[-0.67497965 0.07185978]], RMSD=0.068848
[30]:
# Print alignment info for all chips:
kabsch_results = {}
raw_distances = []
distances = []
for i in range(1, cnt+1):
local = yxi[yxi[:]["i"] == i]
reference = numpy.empty((local.size, 2))
measured = numpy.empty((local.size, 2))
measured[:, 0] = local[:]["x"]
measured[:, 1] = local[:]["y"]
reference[:, 0] = numpy.round((local[:]["x"]-x_min)/step)*step+x_min
reference[:, 1] = numpy.round((local[:]["y"]-y_min)/step)*step+y_min
raw_distances.append(numpy.sqrt(((reference-measured)**2).sum(axis=-1)))
res = kabsch_results[i] = Kabsch(reference, measured)
print(f"Chip: {i:02d} \t Rmsd: {res.rmsd:.4f} \t Angle: {res.angle:.4f}°\t Displacement: {res.translation}")
distances.append(numpy.sqrt(((reference-res.correct(measured))**2).sum(axis=-1)))
Chip: 01 Rmsd: 0.0688 Angle: -0.1671° Displacement: [[-0.67497965 0.07185978]]
Chip: 02 Rmsd: 0.0694 Angle: -0.1780° Displacement: [[-0.74921444 0.03713396]]
Chip: 03 Rmsd: 0.0611 Angle: -0.1825° Displacement: [[-0.65099029 -0.06528506]]
Chip: 04 Rmsd: 0.0611 Angle: -0.1775° Displacement: [[-0.60887022 -0.07475037]]
Chip: 05 Rmsd: 0.0685 Angle: -0.1230° Displacement: [[-0.21554337 -0.96577811]]
Chip: 06 Rmsd: 0.0715 Angle: -0.1200° Displacement: [[-0.29661049 -1.06085904]]
Chip: 07 Rmsd: 0.0811 Angle: -0.1461° Displacement: [[-0.44852491 -0.32922423]]
Chip: 08 Rmsd: 0.0790 Angle: -0.1368° Displacement: [[-0.61495647 -0.56463256]]
Chip: 09 Rmsd: 0.0544 Angle: -0.1940° Displacement: [[-0.7967658 0.08513193]]
Chip: 10 Rmsd: 0.0832 Angle: -0.1774° Displacement: [[-0.71245169 0.00897799]]
Chip: 11 Rmsd: 0.1021 Angle: -0.1751° Displacement: [[-0.60947779 -0.15400862]]
Chip: 12 Rmsd: 0.0718 Angle: -0.1781° Displacement: [[-0.61303755 -0.12631253]]
Chip: 13 Rmsd: 0.0518 Angle: -0.1568° Displacement: [[-0.31260694 -0.3629785 ]]
Chip: 14 Rmsd: 0.0705 Angle: -0.1438° Displacement: [[-0.31433804 -0.55288657]]
Chip: 15 Rmsd: 0.0947 Angle: -0.1401° Displacement: [[-0.31686906 -0.59292664]]
Chip: 16 Rmsd: 0.0910 Angle: -0.1305° Displacement: [[-0.42567601 -0.89338276]]
Chip: 17 Rmsd: 0.0721 Angle: -0.1284° Displacement: [[-0.46335146 -0.51966444]]
Chip: 18 Rmsd: 0.0416 Angle: -0.1373° Displacement: [[-0.53954546 -0.53739966]]
Chip: 19 Rmsd: 0.0701 Angle: -0.1239° Displacement: [[ 0.17706251 -0.62645147]]
Chip: 20 Rmsd: 0.0553 Angle: -0.1442° Displacement: [[ 4.36678268e-05 -3.76929199e-01]]
Chip: 21 Rmsd: 0.0546 Angle: -0.0817° Displacement: [[ 0.55413801 -1.6490182 ]]
Chip: 22 Rmsd: 0.0547 Angle: -0.0866° Displacement: [[ 0.43992059 -1.50747566]]
Chip: 23 Rmsd: 0.0558 Angle: -0.1634° Displacement: [[-0.74590266 0.16987901]]
Chip: 24 Rmsd: 0.0702 Angle: -0.1781° Displacement: [[-1.05131929 0.7248357 ]]
Chip: 25 Rmsd: 0.0594 Angle: -0.1400° Displacement: [[-0.62572742 -0.46928483]]
Chip: 26 Rmsd: 0.0612 Angle: -0.1309° Displacement: [[-0.43446574 -0.53914211]]
Chip: 27 Rmsd: 0.0656 Angle: -0.1452° Displacement: [[-0.0962269 -0.35779115]]
Chip: 28 Rmsd: 0.0499 Angle: -0.1419° Displacement: [[ 0.020441 -0.39043972]]
Chip: 29 Rmsd: 0.0634 Angle: -0.0781° Displacement: [[ 0.63745861 -1.73856753]]
Chip: 30 Rmsd: 0.0573 Angle: -0.0735° Displacement: [[ 0.6717185 -1.87341037]]
Chip: 31 Rmsd: 0.0541 Angle: -0.1618° Displacement: [[-0.70556876 0.06345611]]
Chip: 32 Rmsd: 0.0682 Angle: -0.1717° Displacement: [[-1.01208709 0.43229459]]
Chip: 33 Rmsd: 0.0678 Angle: -0.1815° Displacement: [[-1.61244582 0.11897069]]
Chip: 34 Rmsd: 0.0614 Angle: -0.1882° Displacement: [[-1.67635187 0.23214931]]
Chip: 35 Rmsd: 0.0518 Angle: -0.1539° Displacement: [[-0.49352521 -0.01604175]]
Chip: 36 Rmsd: 0.0583 Angle: -0.1707° Displacement: [[-0.76096941 0.14619773]]
Chip: 37 Rmsd: 0.0618 Angle: -0.1699° Displacement: [[-0.69792471 0.34019815]]
Chip: 38 Rmsd: 0.0456 Angle: -0.1684° Displacement: [[-0.67474355 0.27076164]]
Chip: 39 Rmsd: 0.0432 Angle: -0.1862° Displacement: [[-1.01621339 0.73367301]]
Chip: 40 Rmsd: 0.0591 Angle: -0.1890° Displacement: [[-1.22622669 0.86035063]]
Chip: 41 Rmsd: 0.0403 Angle: -0.1573° Displacement: [[-1.09985312 0.17426807]]
Chip: 42 Rmsd: 0.0703 Angle: -0.1626° Displacement: [[-1.13827772 0.14404882]]
Chip: 43 Rmsd: 0.0609 Angle: -0.1606° Displacement: [[-0.570122 0.1266422]]
Chip: 44 Rmsd: 0.0756 Angle: -0.1683° Displacement: [[-0.66393939 0.17390435]]
Chip: 45 Rmsd: 0.0711 Angle: -0.1762° Displacement: [[-0.81853928 0.50822713]]
Chip: 46 Rmsd: 0.0642 Angle: -0.1815° Displacement: [[-0.94192353 0.62135867]]
Chip: 47 Rmsd: 0.0724 Angle: -0.2028° Displacement: [[-1.40784478 1.24631641]]
Chip: 48 Rmsd: 0.0533 Angle: -0.1945° Displacement: [[-1.31176661 1.01794273]]
Chip: 49 Rmsd: 0.0369 Angle: -0.0883° Displacement: [[1.49863176 0.16646767]]
Chip: 50 Rmsd: 0.0822 Angle: -0.1107° Displacement: [[0.89642789 0.31751451]]
Chip: 51 Rmsd: 0.0633 Angle: -0.2044° Displacement: [[-2.1495324 0.86171123]]
Chip: 52 Rmsd: 0.0634 Angle: -0.1917° Displacement: [[-1.64335742 0.6837618 ]]
Chip: 53 Rmsd: 0.0452 Angle: -0.1136° Displacement: [[ 0.93232384 -0.98275464]]
Chip: 54 Rmsd: 0.0491 Angle: -0.1206° Displacement: [[ 0.74155725 -0.79061826]]
Chip: 55 Rmsd: 0.0585 Angle: -0.2007° Displacement: [[-1.86969417 1.61932506]]
Chip: 56 Rmsd: 0.0670 Angle: -0.1893° Displacement: [[-1.60803861 1.33258926]]
Chip: 57 Rmsd: 0.1030 Angle: -0.0903° Displacement: [[1.36871629 0.35389081]]
Chip: 58 Rmsd: 0.0564 Angle: -0.0855° Displacement: [[1.69019632 0.28538168]]
Chip: 59 Rmsd: 0.0622 Angle: -0.2039° Displacement: [[-2.21352204 0.98072702]]
Chip: 60 Rmsd: 0.0409 Angle: -0.2061° Displacement: [[-2.18576859 1.0705361 ]]
Chip: 61 Rmsd: 0.0490 Angle: -0.1186° Displacement: [[ 0.72715909 -0.71879601]]
Chip: 62 Rmsd: 0.0568 Angle: -0.0928° Displacement: [[ 1.71978044 -1.34312101]]
Chip: 63 Rmsd: 0.0541 Angle: -0.1894° Displacement: [[-1.54607885 1.45525824]]
Chip: 64 Rmsd: 0.0612 Angle: -0.1988° Displacement: [[-1.87932057 1.79230351]]
[31]:
ndistances = numpy.concatenate(distances)
nraw_distances = numpy.concatenate(raw_distances)
fig, ax = subplots()
ax.hist(nraw_distances, bins=100, label="raw positions")
ax.hist(ndistances, bins=100, label="refined positions")
ax.set_title("Histogram of displacement")
ax.set_xlabel("Distance in pixels")
ax.set_ylabel("Number of spots")
ax.legend()
pass
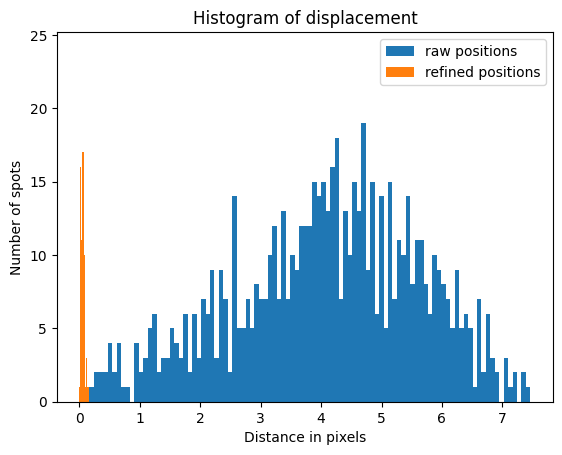
Reconstruction of the pixel position
The pixel position can be obtained from the standard Pilatus detector. Each module is then displaced according to the fitted values.
[32]:
%%time
pixel_coord = pyFAI.detector_factory("Eiger2CdTe_4M").get_pixel_corners().astype(numpy.float64)
pixel_coord_raw = pixel_coord.copy()
for module in range(1, cnt+1):
# Extract the pixel corners for one module
module_idx = numpy.where(filled_mid == module)
one_module = pixel_coord_raw[module_idx]
#retrieve the fitted values
res = kabsch_results[module]
#z = one_module[...,0]
y = one_module[...,1].ravel()/eiger2.pixel1
x = one_module[...,2].ravel()/eiger2.pixel2
xy_initial = numpy.vstack((x, y)).T
xy_aligned = res.correct(xy_initial)
one_module[...,1] = (xy_aligned[:,1] * eiger2.pixel1).reshape(one_module.shape[:-1])
one_module[...,2] = (xy_aligned[:,0] * eiger2.pixel2).reshape(one_module.shape[:-1])
#Update the array
pixel_coord[module_idx] = one_module
CPU times: user 7.15 s, sys: 139 ms, total: 7.28 s
Wall time: 1.9 s
[33]:
# displacement for every pixel corner (before/after global displacement):
displ_refined = numpy.sqrt(((pixel_coord - pixel_coord_raw)**2).sum(axis=-1))/eiger2.pixel1
global_ref = Kabsch(pixel_coord_raw.reshape((-1, 3)), pixel_coord.reshape((-1, 3)))
new_pixel_coord = global_ref.correct(pixel_coord.reshape((-1, 3))).reshape(pixel_coord_raw.shape)
displ_aligned = numpy.sqrt(((new_pixel_coord - pixel_coord_raw)**2).sum(axis=-1))/eiger2.pixel1
[34]:
fig, ax = subplots()
ax.hist(displ_refined.ravel(), 100, label="refined before alignment")
ax.hist(displ_aligned.ravel(), 100, label="refined after alignement")
ax.set_title("Displacement of pixel corners versus a regular pixel layout")
ax.set_xlabel("Distance in pixels")
ax.set_ylabel("Number of corners of pixels")
ax.legend()
pass
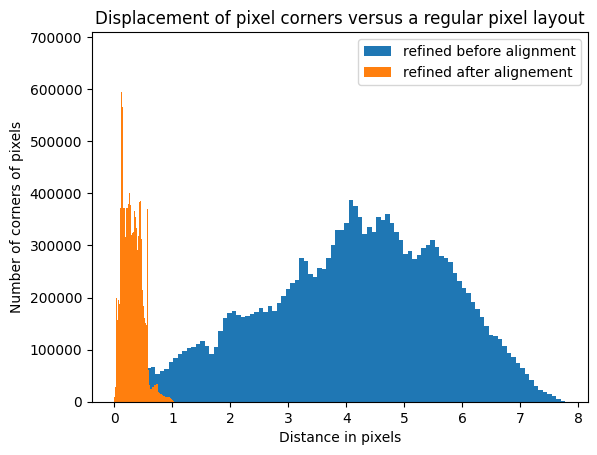
Validation of the distortion
To validate the new pixel layout, we can use the new grid to calculate the spot postition in space and look how well aligned they are.
First we build a function which performes the bilinear interpolation of any detector coordinate (return a 3D position). This function is then used to calculate the position for the original grid and for the corrected grid.
As previouly, all spot distances are calculated and histogrammed. The standard deviation is used to evaluate how much was gained.
[35]:
def intepolate_3d(yx, coord=pixel_coord_raw):
y,x = yx
X = int(x)
Y = int(y)
pixel = coord[Y,X]
#print(pixel)
dx = x - X
dy = y - Y
res = pixel[0]*(1.0-dx)*(1.0-dy)+\
pixel[3]*dx*(1.0-dy)+\
pixel[1]*(1.0-dx)*dy+\
pixel[2]*dx*dy
return res
intepolate_3d((0.99,0.01))
[35]:
array([0.00000000e+00, 7.42500035e-05, 7.50000036e-07])
[36]:
raw_pixel_64 = pixel_coord_raw.astype("float64")/eiger2.pixel1
new_pixel_64 = new_pixel_coord.astype("float64")/eiger2.pixel1
spot3d_raw = numpy.array([intepolate_3d(i, coord=raw_pixel_64) for i in ref_peaks])
spot3d_ref = numpy.array([intepolate_3d(i, coord=new_pixel_64) for i in ref_peaks])
dist_raw = distance_matrix(spot3d_raw, spot3d_raw)
valid_raw = dist_raw[numpy.logical_and(65<dist_raw, dist_raw<70)]
dist_ref = distance_matrix(spot3d_ref, spot3d_ref)
valid_ref = dist_ref[numpy.logical_and(65<dist_ref, dist_ref<70)]
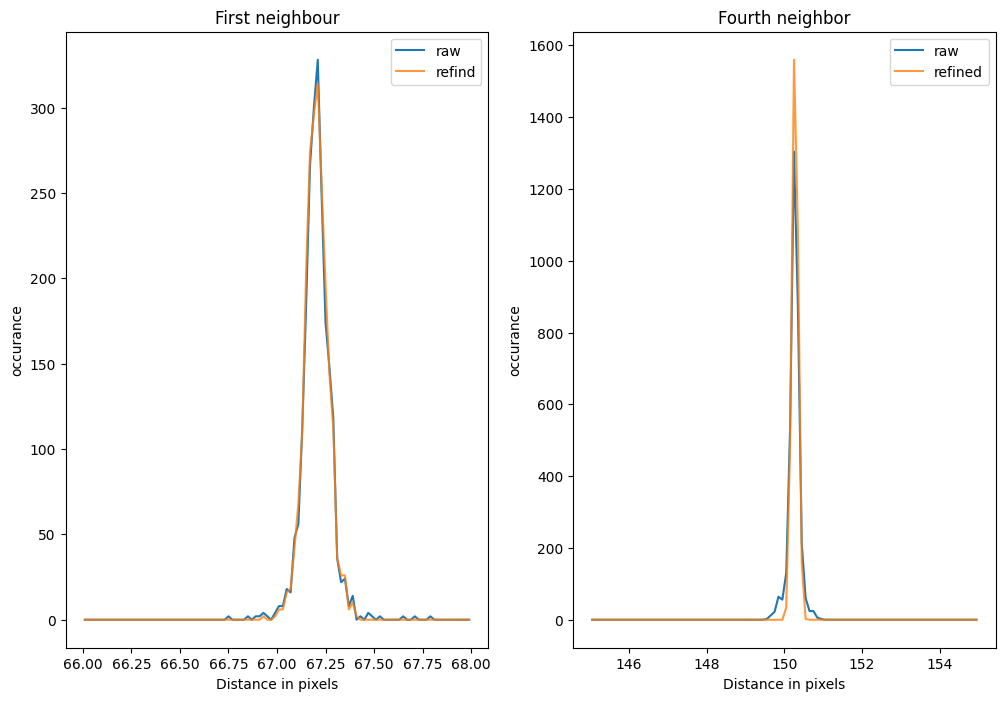
[37]:
fig,ax = subplots(1, 2, figsize=(12,8))
valid1_raw = dist_raw[numpy.logical_and(65<dist_raw, dist_raw<70)]
valid1_ref = dist_ref[numpy.logical_and(65<dist_ref, dist_ref<70)]
h1_raw = numpy.histogram(valid1_raw, 100, range=(66, 68))
h1_ref = numpy.histogram(valid1_ref, 100, range=(66, 68))
x = 0.5*(h1_raw[1][1:]+h1_raw[1][:-1])
ax[0].plot(x, h1_raw[0], label="raw")
ax[0].plot(x, h1_ref[0], label="refind", alpha=0.8)
ax[0].legend()
ax[0].set_title("First neighbour")
ax[0].set_xlabel("Distance in pixels")
ax[0].set_ylabel("occurance")
valid2_raw = dist_raw[numpy.logical_and(145<dist_raw, dist_raw<155)]
valid2_ref = dist_ref[numpy.logical_and(145<dist_ref, dist_ref<155)]
h2_raw = numpy.histogram(valid2_raw, 100, range=(145, 155))
h2_ref = numpy.histogram(valid2_ref, 100, range=(145, 155))
x = 0.5*(h2_raw[1][1:]+h2_raw[1][:-1])
ax[1].plot(x, h2_raw[0], label="raw")
ax[1].plot(x, h2_ref[0], label="refined", alpha=0.8)
ax[1].legend()
ax[1].set_title("Fourth neighbor")
ax[1].set_xlabel("Distance in pixels")
ax[1].set_ylabel("occurance")
print("Distance of first neighbor before: "+f"{valid1_raw.mean():.4f} ± {valid1_raw.std():.4f} after: {valid1_ref.mean():.4f} ± {valid1_ref.std():.4f}")
print("Distance of fourth neighbor before: "+f"{valid2_raw.mean():.4f} ± {valid2_raw.std():.4f} after: {valid2_ref.mean():.4f} ± {valid2_ref.std():.4f}")
Distance of first neighbor before: 67.2044 ± 0.0740 after: 67.2035 ± 0.0607
Distance of fourth neighbor before: 150.2610 ± 0.1454 after: 150.2759 ± 0.0743
[38]:
#Saving of the result as a distortion file usable in pyFAI
dest = "Eiger2CdTe_4M_ID11.h5"
if os.path.exists(dest):
os.unlink(dest)
eiger2.set_pixel_corners(new_pixel_coord.astype(numpy.float32))
eiger2.mask = eiger2.calc_mask() + flat>(flat.max()*0.9)
eiger2.save(dest)
Conclusion
The distortion measured on the Eiger2 CdTe 4M detector for ID11 are small (<1 pixel, 75µm) but measurable and can be corrected to precision of 5µm using the displacement matrix.
[39]:
print(f"Total execution time: {time.perf_counter()-start_time:.3f}s")
Total execution time: 67.684s