Exercise: HPLC experiment

Credits ESRF/BM29 beamline

Introduction

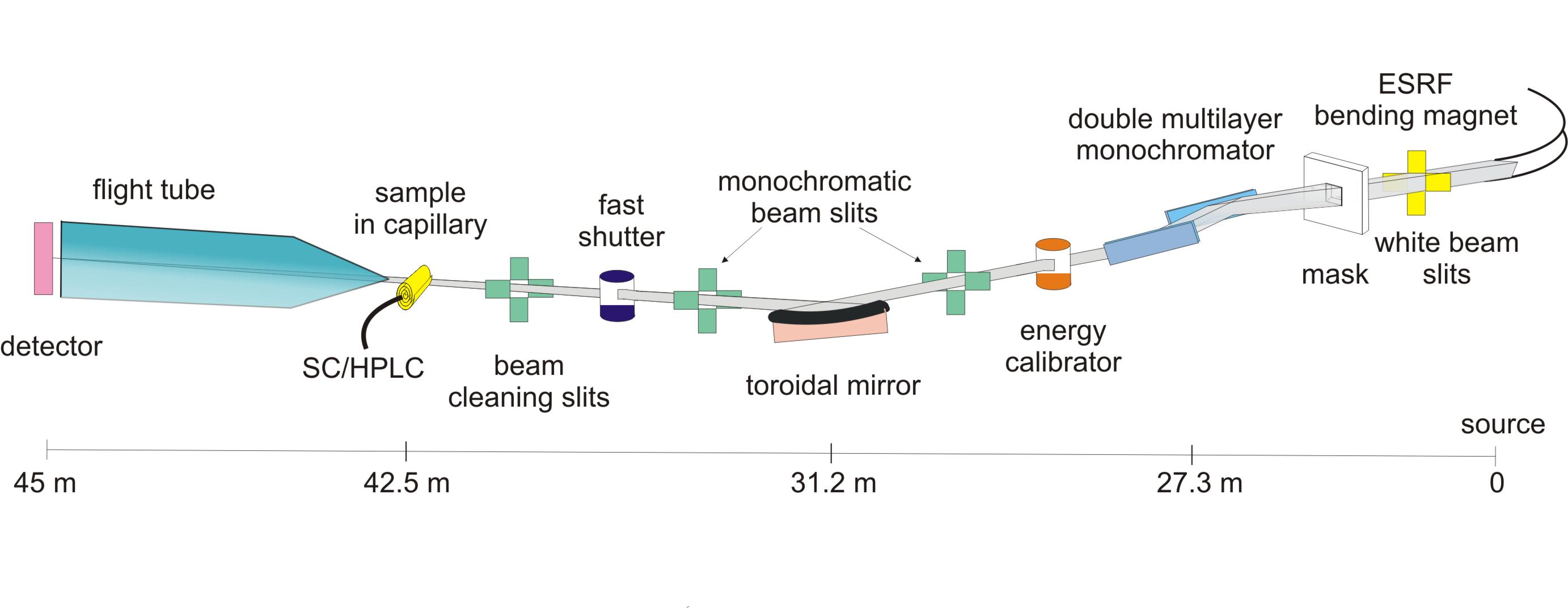
Process data from a High-performance Liquid Chromatography (HPLC) experiment performed on ESRF/BM29 BioSAXS beamline.

The sample is Bovin Serum Albumin (BSA) protein (used as a standard sample):

The buffer and sample are exposed to X-rays while passing through a capillary. Images are recorded over time (400 in this experiment) and an azimuthal integration is performed for each image with pyFAI.

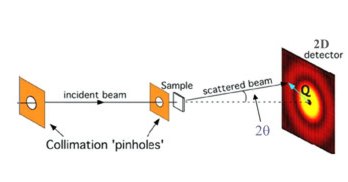
This results in 400 curves of integrated intensities I for 1000 values of q. Those I values are stored as a 2D dataset of shape (400, 1000) in the intensities.npy file. The q values are stored in the q.txt file.

At first, only the buffer is passing through the capillary, then sample + buffer and finally buffer again.

The goal is to extract the intensity contributed by the sample. The steps are:

1. Separate integrated intensities corresponding to buffer+sample from those corresponding to buffer only
2. Estimate the buffer and the sample + buffer intensities by averaging the selected integrated intensities
3. Remove the buffer background from sample + buffer

Part I

import numpy as np

Load data

Load intensities I from the intensities.npy file and q values from the q.txt file.

intensities = # TODO
q = # TODO

Plot data

%matplotlib widget
# This requires ipympl
# Or for non-interactive plots: %matplotlib inline

from matplotlib import pyplot as plt

# Plot the intensities
import matplotlib.colors as colors

fig = plt.figure()
plt.imshow(intensities, norm=colors.LogNorm(), aspect="auto")
  
# Note: with latest version of matplotlib:    
# plt.imshow(intensities, norm="log", aspect="auto")

# Plot one curve
fig = plt.figure()
plt.plot(q, intensities[0])
plt.yscale("log")  # Use logarithmic scale for y axis

Part II

Average of all azimuthal integrations

Compute the averaged intensity over intensities for each value of q

intensities_mean = # TODO

fig = plt.figure()
plt.plot(q, intensities_mean)
plt.xlabel("q")
plt.ylabel("I")
plt.yscale("log")
plt.title("Average intensity")  # Add a title to the plot

Note: This is not meaningful, the buffer and sample + buffer cases should be separated.

Summed intensity of each azimuthal integration

Compute the sum of each row of the intensities data

intensities_per_frame = # TODO

fig = plt.figure()
plt.plot(intensities_per_frame)
plt.xlabel("Frame ID")
plt.ylabel("I")

Part III

Separate sample + buffer from buffer only

Select buffer and sample + buffer intensities by using a threshold over intensities_per_frame.

buffer = # TODO

sample_buffer = # TODO

print("buffer shape:", buffer.shape, "sample_buffer shape:", sample_buffer.shape)

Average sample + buffer and buffer intensities

Compute the average of azimuthal integrations of buffer for each q.

buffer_mean = # TODO

Do the same for sample_buffer.

sample_buffer_mean = # TODO

fig = plt.figure()
plt.plot(q, buffer_mean, 'black', q, sample_buffer_mean, 'red')
plt.title("buffer and sample + buffer average")
plt.xlabel("q")
plt.ylabel("I")
plt.yscale("log")

Remove buffer background

Compute the different between sample_buffer_mean and buffer_mean.

sample = # TODO

fig = plt.figure()
plt.plot(q, sample)
plt.yscale("log")

Solution

...

# Part I

import numpy as np

# Load data
intensities = np.load("intensities.npy")
q = np.loadtxt("q.txt")

# Part II

# Average of all azimuthal integrations
intensities_mean = np.mean(intensities, axis=0)

# Summed intensity of each azimuthal integration
intensities_per_frame = np.sum(intensities, axis=1)

# Part III

# Separate sample + buffer from buffer only
# 1. with thresholds
buffer_mask = intensities_per_frame < 32500
buffer = intensities[buffer_mask]
sample_buffer_mask = frames_intensities > 33000
sample_buffer = intensities[sample_buffer_mask]
# 2. With slicing
buffer = intensities[:200]
sample_buffer = intensities[270:340]

# Average sample + buffer and buffer intensities
buffer_mean = np.mean(buffer, axis=0)
sample_buffer_mean = np.mean(sample_buffer, axis=0)

# Remove buffer background
sample = sample_buffer_mean - buffer_mean