Geometry

Some words on experiment geometry

The following drawing is a fluorescence experiment geometry as seen by FreeART (with 1 fluorescence detector only)

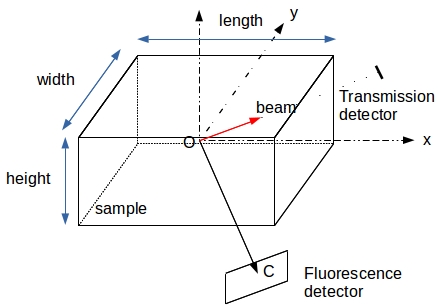
In FreeART, the axis origin is the sample center (point O). The sample is supposed to be fixed and it is the incoming beam and detector(s) which rotate around it. The fluorescence detector center is the point named C.

Today (September 2016), FreeART is doing its computation in 2D (slice reconstruction) even if some of its input parameters in term of geometries are 3D values (x, y and z). For 3D volume, the dimension on the x axis is known as the length, the y axis dimension is the width while the z axis dimension is the height.

In 2D, the geometry becomes

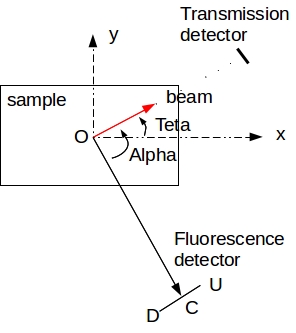
In 2D, the fluorescence detector becomes a simple line. C is the middle of this line which starts at point D and ends at point U. The angle theta is the angle between the incoming beam and the x axis while the angle alpha is the angle between \(\vec{OC}\) and the incoming beam.

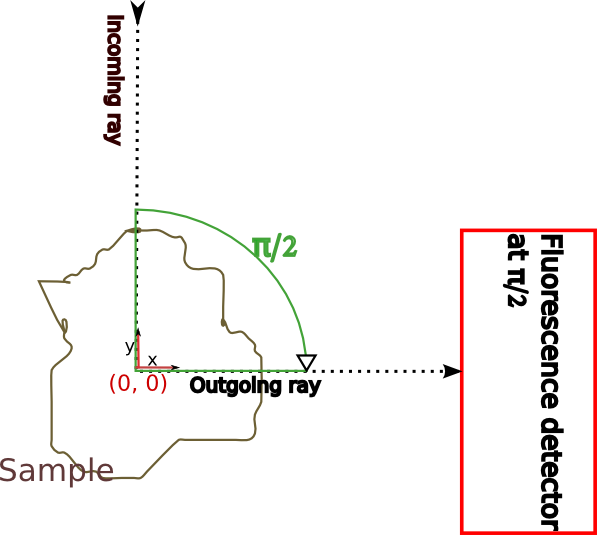
The incoming beam which pass by the center of the space and have an angle of 0 will come from (0, infinity, 0) and along the direction vector (0, -1, 0 ). Angles unit is radian. The angle are clockwise oriented. So if we set an angle of \(\frac{pi}{2}\) then the incoming ray which will pass by the center of the space will came from (infinity, 0, 0) and with a direction of (-1, 0, 0 )