Calibration of the 9-Mythen detector at the Cristal beamline at Soleil
Mythen detectors are 1D-strip detector sold by Dectris. On the Cristal beamline at Soleil, 9 of them are mounted on the goniometer.
This notebook explains how to calibrate precisely their position (including the wavelength used) as function of the goniometer position.
All input data are provided in a Nexus file wich contrains both the (approximate) energy, the goniometer positions (500 points have been measured) and the measured signal.
As pyFAI is not made for 1D data, the Mythen detector will be considered as a 1x1280 image.
We start by importing a whole bunch of modules:
[1]:
%matplotlib inline
# use `widget` for better user experience; `inline` is for documentation generation
[2]:
from collections import OrderedDict
from matplotlib import pyplot as plt
import numpy
import os
import h5py
from silx.resources import ExternalResources
from pyFAI import goniometer
from pyFAI.detectors import Detector
from pyFAI.goniometer import ExtendedTransformation, GoniometerRefinement
from pyFAI.control_points import ControlPoints
from pyFAI.geometryRefinement import GeometryRefinement
from pyFAI.gui import jupyter
from pyFAI.units import hc
from pyFAI.calibrant import get_calibrant
from pyFAI.containers import Integrate1dResult
import ipywidgets as widgets
from scipy.signal import find_peaks_cwt
from scipy.interpolate import interp1d
from scipy.optimize import bisect, minimize
from scipy.spatial import distance_matrix
import time
start_time = time.time()
/home/jerome/.venv/py311/lib/python3.11/site-packages/pyopencl/cache.py:495: CompilerWarning: Non-empty compiler output encountered. Set the environment variable PYOPENCL_COMPILER_OUTPUT=1 to see more.
_create_built_program_from_source_cached(
/home/jerome/.venv/py311/lib/python3.11/site-packages/pyopencl/cache.py:499: CompilerWarning: Non-empty compiler output encountered. Set the environment variable PYOPENCL_COMPILER_OUTPUT=1 to see more.
prg.build(options_bytes, devices)
[3]:
#Nota: Useful to configure a proxy if you are behind a firewall
#os.environ["http_proxy"] = "http://proxy.company.fr:3128"
downloader = ExternalResources("detector_calibration", "http://www.silx.org/pub/pyFAI/gonio/")
mythen_ring_file = downloader.getfile("LaB6_17keV_att3_tth2C_24_01_2018_19-43-20_1555.nxs")
The data file can be downoaded from: http://www.silx.org/pub/pyFAI/gonio/LaB6_17keV_att3_tth2C_24_01_2018_19-43-20_1555.nxs
[4]:
#Open the Nexus file and retrieve the actual positions:
h5 = h5py.File(mythen_ring_file, mode="r")
position = h5["/LaB6_17keV_att3_1555/scan_data/actuator_1_1"][:]
print("Positions: ", position[:5], "...")
Positions: [90.00000001 89.79994445 89.5998889 89.39994445 89.19994445] ...
[5]:
#Read all data
data = {}
ds_names = []
for idx in range(1,13):
name = "data_%02i"%idx
ds = h5["/LaB6_17keV_att3_1555/scan_data/"+name][:]
print(name, ds.shape)
if ds.shape[1]<2000:
#Keep only the single modules
data[name] = ds
ds_names.append(name)
print(ds_names)
data_01 (501, 5120)
data_02 (501, 1280)
data_03 (501, 1280)
data_04 (501, 1280)
data_05 (501, 1280)
data_06 (501, 5120)
data_07 (501, 1280)
data_08 (501, 1280)
data_09 (501, 1280)
data_10 (501, 1280)
data_11 (501, 1280)
data_12 (501, 1280)
['data_02', 'data_03', 'data_04', 'data_05', 'data_07', 'data_08', 'data_09', 'data_10', 'data_11', 'data_12']
[6]:
#Define a Mythen-detector mounted vertically:
class MythenV(Detector):
"Verical Mythen dtrip detector from Dectris"
aliases = ["MythenV 1280"]
force_pixel = True
MAX_SHAPE = (1280, 1)
def __init__(self,pixel1=50e-6, pixel2=8e-3):
super(MythenV, self).__init__(pixel1=pixel1, pixel2=pixel2)
[7]:
#Define all modules as single detectors of class MythenV.
# Each one has a mask defined from dummy-values in the dataset
modules = {}
for name, ds in data.items():
one_module = MythenV()
mask = ds[0]<0
#discard the first 20 and last 20 pixels as their intensities are less reliable
mask[:20] = True
mask[-20:] = True
one_module.mask = mask.reshape(-1,1)
modules[name] = one_module
for k,v in modules.items():
print(k, v.name)
data_02 MythenV 1280
data_03 MythenV 1280
data_04 MythenV 1280
data_05 MythenV 1280
data_07 MythenV 1280
data_08 MythenV 1280
data_09 MythenV 1280
data_10 MythenV 1280
data_11 MythenV 1280
data_12 MythenV 1280
[8]:
# Define a peak-picking function based on the dataset-name and the frame_id:
def peak_picking(module_name, frame_id,
threshold=500):
"""Peak-picking base on find_peaks_cwt from scipy plus
second-order tailor exapention refinement for sub-pixel resolution.
The half-pixel offset is accounted here, i.e pixel #0 has its center at 0.5
"""
module = modules[module_name]
msk = module.mask.ravel()
spectrum = data[module_name][frame_id]
guess = find_peaks_cwt(spectrum, [20])
valid = numpy.logical_and(numpy.logical_not(msk[guess]),
spectrum[guess]>threshold)
guess = guess[valid]
#Based on maximum is f'(x) = 0 ~ f'(x0) + (x-x0)*(f''(x0))
df = numpy.gradient(spectrum)
d2f = numpy.gradient(df)
bad = d2f==0
d2f[bad] = 1e-10 #prevent devision by zero. Discared later on
cor = df / d2f
cor[abs(cor)>1] = 0
cor[bad] = 0
ref = guess - cor[guess] + 0.5 #half a pixel offset
x = numpy.zeros_like(ref) + 0.5 #half a pixel offset
return numpy.vstack((ref,x)).T
%timeit peak_picking(ds_names[0], 93)
print(peak_picking(ds_names[0], 93))
13 ms ± 69.2 µs per loop (mean ± std. dev. of 7 runs, 100 loops each)
[[287.06072343 0.5 ]]
[9]:
nrj = h5["/LaB6_17keV_att3_1555/CRISTAL/Monochromator/energy"][0]
wl = hc / nrj *1e-10
print("Energy (keV): ",nrj, "\nWavelength (A): ",wl)
LaB6 = get_calibrant("LaB6")
LaB6.wavelength = wl
print(LaB6)
Energy (keV): 17.027082549190933
Wavelength (A): 7.281587910025816e-11
LaB6 Calibrant with 109 reflections at wavelength 7.281587910025816e-11
[10]:
#This cell defines the transformation of coordinates for a simple goniometer mounted vertically.
trans = ExtendedTransformation(dist_expr="dist",
poni1_expr="poni1",
poni2_expr="poni2",
rot1_expr="rot1",
rot2_expr="pi*(offset+scale*angle)/180.",
rot3_expr="0.0",
wavelength_expr="hc/nrj*1e-10",
param_names=["dist", "poni1", "poni2", "rot1", "offset", "scale", "nrj"],
pos_names=["angle"],
constants={"hc": hc})
[11]:
def get_position(idx):
"Returns the postion of the goniometer for the given frame_id"
return position[idx]
#Approximate offset for the module #0 at 0°
print("Approximated offset for the first module: ",get_position(36))
Approximated offset for the first module: 82.79994445106844
[12]:
#This interactive plot lets one visualize any spectra acquired by any module
fig, ax = plt.subplots()
line = ax.plot(data[ds_names[0]][250])[0]
ligne = plt.Line2D(xdata=[640,640], ydata=[-500, 1000], figure=fig, linestyle="--", color='red', axes=ax)
ax.add_line(ligne)
ax.set_title("spectrum")
fig.show()
def update(module_id, frame_id):
spectrum = data[ds_names[module_id]][frame_id]
line.set_data(numpy.arange(spectrum.size), spectrum)
ax.set_title("Module %i, Frame %i"%(module_id, frame_id))
fig.canvas.draw()
interactive_plot = widgets.interactive(update,
module_id=(0, len(data)-1),
frame_id=(0, data[ds_names[0]].shape[0]-1))
display(interactive_plot)
/tmp/ipykernel_367778/505442400.py:8: UserWarning: Matplotlib is currently using module://matplotlib_inline.backend_inline, which is a non-GUI backend, so cannot show the figure.
fig.show()
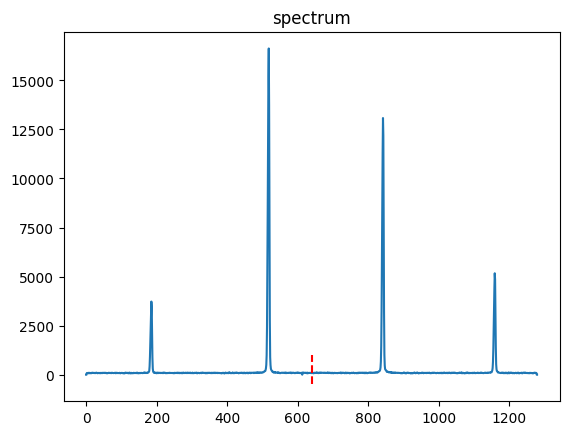
[13]:
#Work with the first module corresponding to:
name = ds_names[0]
print(name)
ds = data[name]
module = modules[name]
#Use the previous widget to select:
## the index where the beam-center is in the middle of the module
zero_pos = 36
## The frame index where the first LaB6 peak enters the right-hand side of the spectrum
peak_zero_start = 74
## The frame index where this first LaB6 leaves the spectrum or the second LaB6 peak appears:
peak_zero_end = 94
# The frames between peak_zero_start and peak_zero_end will be used to calibrate roughly the goniometer
# and used later for finer peak extraction
data_02
[14]:
param0 = {"dist": 0.72,
"poni1": 640*50e-6,
"poni2": 4e-3,
"rot1":0,
"offset": -get_position(zero_pos),
"scale":1,
"nrj": nrj}
#Lock enegy for now and a couple of other parameters
bounds0 = {"nrj": (nrj, nrj),
"dist": (0.71, 0.73),
"poni2": (4e-3, 4e-3),
"rot1": (0,0),
"scale":(1,1),
}
gonioref0 = GoniometerRefinement(param0,
get_position,
trans,
detector=module,
wavelength=wl,
bounds=bounds0
)
goniometers = {name: gonioref0}
print(gonioref0)
GoniometerRefinement with 0 geometries labeled: .
[15]:
# Extract the frames where only the peak zero from LaB6 is present.
for i in range(peak_zero_start, peak_zero_end):
cp = ControlPoints(calibrant=LaB6, wavelength=wl)
peak = peak_picking(name, i)
if len(peak)!=1:
continue
cp.append([peak[0]], ring=0)
img = ds[i].reshape((-1,1)) #Images are vertical ... transpose the spectrum
sg = gonioref0.new_geometry("%s_%04i"%(name,i),
image=img,
metadata=i,
control_points=cp,
calibrant=LaB6)
sg.geometry_refinement.data = numpy.array(cp.getList())
print(gonioref0)
print("Residual error before fit:")
print(gonioref0.chi2())
GoniometerRefinement with 20 geometries labeled: data_02_0074, data_02_0075, data_02_0076, data_02_0077, data_02_0078, data_02_0079, data_02_0080, data_02_0081, data_02_0082, data_02_0083, data_02_0084, data_02_0085, data_02_0086, data_02_0087, data_02_0088, data_02_0089, data_02_0090, data_02_0091, data_02_0092, data_02_0093.
Residual error before fit:
6.737408475887519e-07
[16]:
#First refinement:
gonioref0.refine2()
Cost function before refinement: 6.737408475887519e-07
[ 7.20000000e-01 3.20000000e-02 4.00000000e-03 0.00000000e+00
-8.27999445e+01 1.00000000e+00 1.70270825e+01]
message: Optimization terminated successfully
success: True
status: 0
fun: 2.490988846910722e-11
x: [ 7.200e-01 3.141e-02 4.000e-03 0.000e+00 -8.280e+01
1.000e+00 1.703e+01]
nit: 2
jac: [ 1.584e-07 2.919e-08 nan nan 3.427e-11
nan nan]
nfev: 9
njev: 2
Cost function after refinement: 2.490988846910722e-11
GonioParam(dist=0.719994724358983, poni1=0.031408577292064206, poni2=0.004, rot1=0.0, offset=-82.79995188659902, scale=1.0, nrj=17.027082549190933)
maxdelta on: poni1 (1) 0.032 --> 0.031408577292064206
[16]:
array([ 7.19994724e-01, 3.14085773e-02, 4.00000000e-03, 0.00000000e+00,
-8.27999519e+01, 1.00000000e+00, 1.70270825e+01])
[17]:
#Here we extract all spectra for peaks,
# If there are as many peaks as expected from the theoritical LaB6. perform the assignment.
#Peaks from LaB6:
tths = LaB6.get_2th()
for i in range(peak_zero_end, ds.shape[0]):
peak = peak_picking(name, i)
ai=gonioref0.get_ai(get_position(i))
tth = ai.array_from_unit(unit="2th_rad", scale=False)
tth_low = tth[20]
tth_hi = tth[-20]
ttmin, ttmax = min(tth_low, tth_hi), max(tth_low, tth_hi)
valid_peaks = numpy.logical_and(ttmin<=tths, tths<ttmax)
cnt = valid_peaks.sum()
if (len(peak) == cnt):
cp = ControlPoints(calibrant=LaB6, wavelength=wl)
#revert the order of assignment if needed !!
if tth_hi < tth_low:
peak = peak[-1::-1]
for p, r in zip(peak, numpy.where(valid_peaks)[0]):
#print(p,r)
cp.append([p], ring=r)
img = ds[i].reshape((-1,1))
sg = gonioref0.new_geometry("%s_%04i"%(name,i),
image=img,
metadata=i,
control_points=cp,
calibrant=LaB6)
sg.geometry_refinement.data = numpy.array(cp.getList())
#print(sg.label, len(sg.geometry_refinement.data))
#print(gonioref0)
print(" Number of peaks found and used for refinement")
print(sum([len(sg.geometry_refinement.data) for sg in gonioref0.single_geometries.values()]))
print("Residual error before fitting: ", gonioref0.chi2())
Number of peaks found and used for refinement
1203
Residual error before fitting: 3.118662178645907e-06
[18]:
gonioref0.refine2()
Cost function before refinement: 3.118662178645907e-06
[ 7.19994724e-01 3.14085773e-02 4.00000000e-03 0.00000000e+00
-8.27999519e+01 1.00000000e+00 1.70270825e+01]
message: Optimization terminated successfully
success: True
status: 0
fun: 2.7342490266357463e-06
x: [ 7.231e-01 3.185e-02 4.000e-03 0.000e+00 -8.280e+01
1.000e+00 1.703e+01]
nit: 7
jac: [-5.582e-08 -3.618e-10 nan nan 6.365e-10
nan nan]
nfev: 30
njev: 7
Cost function after refinement: 2.7342490266357463e-06
GonioParam(dist=0.7230953421817191, poni1=0.03184537030470006, poni2=0.004, rot1=0.0, offset=-82.7999466162549, scale=1.0, nrj=17.027082549190933)
maxdelta on: dist (0) 0.719994724358983 --> 0.7230953421817191
[18]:
array([ 7.23095342e-01, 3.18453703e-02, 4.00000000e-03, 0.00000000e+00,
-8.27999466e+01, 1.00000000e+00, 1.70270825e+01])
[19]:
gonioref0.set_bounds("poni1", -1, 1)
gonioref0.set_bounds("poni2", -1, 1)
gonioref0.set_bounds("rot1", -1, 1)
gonioref0.set_bounds("scale", 0.9, 1.1)
gonioref0.refine2()
Cost function before refinement: 2.7342490266357463e-06
[ 7.23095342e-01 3.18453703e-02 4.00000000e-03 0.00000000e+00
-8.27999466e+01 1.00000000e+00 1.70270825e+01]
message: Optimization terminated successfully
success: True
status: 0
fun: 2.689172533892251e-06
x: [ 7.231e-01 3.205e-02 3.985e-03 1.095e-05 -8.280e+01
9.994e-01 1.703e+01]
nit: 4
jac: [-5.145e-07 -1.241e-07 5.957e-07 -4.287e-07 -9.297e-10
-8.539e-08 nan]
nfev: 28
njev: 4
Cost function after refinement: 2.689172533892251e-06
GonioParam(dist=0.7230962438566039, poni1=0.03205370080101193, poni2=0.003984854883002208, rot1=1.0947770664950588e-05, offset=-82.79994398900047, scale=0.9994150576486731, nrj=17.027082549190933)
maxdelta on: scale (5) 1.0 --> 0.9994150576486731
[19]:
array([ 7.23096244e-01, 3.20537008e-02, 3.98485488e-03, 1.09477707e-05,
-8.27999440e+01, 9.99415058e-01, 1.70270825e+01])
[20]:
# Perform the azimuthal intgration of all data for the first module:
mg = gonioref0.get_mg(position)
mg.radial_range = (0, 95)
images = [i.reshape(-1, 1) for i in ds]
res_mg = mg.integrate1d(images, 50000)
results={name: res_mg}
print(results)
{'data_02': (array([9.50000113e-04, 2.85000034e-03, 4.75000057e-03, ...,
9.49952613e+01, 9.49971613e+01, 9.49990613e+01]), array([0.00000000e+00, 0.00000000e+00, 0.00000000e+00, ...,
1.27158634e+08, 1.31904151e+08, 1.31268033e+08]))}
[21]:
# Plot the integrated pattern vs expected peak positions:
LaB6_new = get_calibrant("LaB6")
LaB6_new.wavelength = hc/gonioref0.param[-1]*1e-10
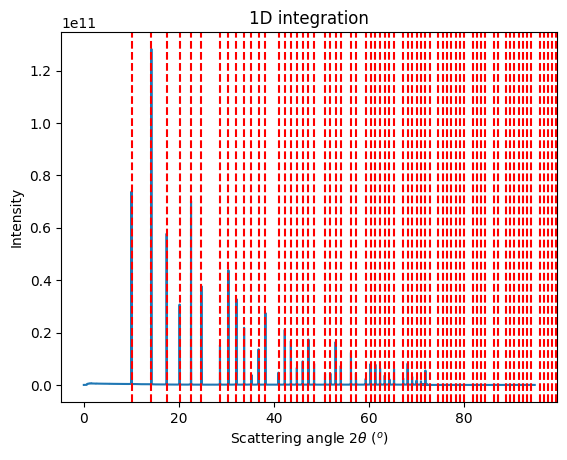
p = jupyter.plot1d(res_mg, calibrant=LaB6_new)
p.figure.show()
/tmp/ipykernel_367778/954410272.py:6: UserWarning: Matplotlib is currently using module://matplotlib_inline.backend_inline, which is a non-GUI backend, so cannot show the figure.
p.figure.show()
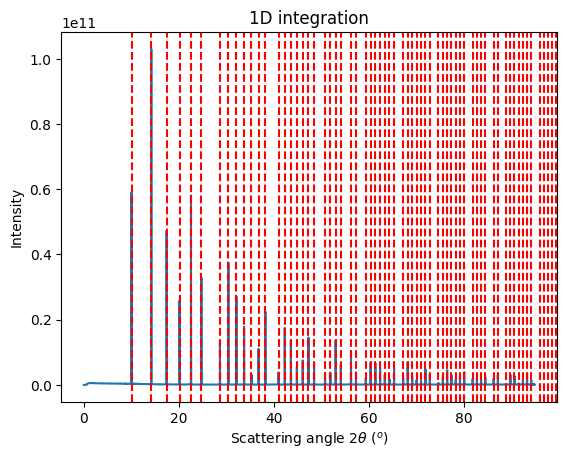
[22]:
#Peak profile function based on a bilinear interpolations:
def calc_fwhm(integrate_result, calibrant, tth_min=None, tth_max=None):
"calculate the tth position and FWHM for each peak"
delta = integrate_result.intensity[1:] - integrate_result.intensity[:-1]
maxima = numpy.where(numpy.logical_and(delta[:-1]>0, delta[1:]<0))[0]
minima = numpy.where(numpy.logical_and(delta[:-1]<0, delta[1:]>0))[0]
maxima += 1
minima += 1
tth = []
FWHM = []
if tth_min is None:
tth_min = integrate_result.radial[0]
if tth_max is None:
tth_max = integrate_result.radial[-1]
for tth_rad in calibrant.get_2th():
tth_deg = tth_rad*integrate_result.unit.scale
if (tth_deg<=tth_min) or (tth_deg>=tth_max):
continue
idx_theo = abs(integrate_result.radial-tth_deg).argmin()
id0_max = abs(maxima-idx_theo).argmin()
id0_min = abs(minima-idx_theo).argmin()
I_max = integrate_result.intensity[maxima[id0_max]]
I_min = integrate_result.intensity[minima[id0_min]]
tth_maxi = integrate_result.radial[maxima[id0_max]]
I_thres = (I_max + I_min)/2.0
if minima[id0_min]>maxima[id0_max]:
if id0_min == 0:
min_lo = integrate_result.radial[0]
else:
min_lo = integrate_result.radial[minima[id0_min-1]]
min_hi = integrate_result.radial[minima[id0_min]]
else:
if id0_min == len(minima) -1:
min_hi = integrate_result.radial[-1]
else:
min_hi = integrate_result.radial[minima[id0_min+1]]
min_lo = integrate_result.radial[minima[id0_min]]
f = interp1d(integrate_result.radial, integrate_result.intensity-I_thres)
try:
tth_lo = bisect(f, min_lo, tth_maxi)
tth_hi = bisect(f, tth_maxi, min_hi)
except:
pass
else:
FWHM.append(tth_hi-tth_lo)
tth.append(tth_deg)
return tth, FWHM
[23]:
# Peak error:
def calc_peak_error(integrate_result, calibrant, tth_min=10, tth_max=95):
"calculate the tth position and FWHM for each peak"
peaks = find_peaks_cwt(integrate_result.intensity, [10])
df = numpy.gradient(integrate_result.intensity)
d2f = numpy.gradient(df)
bad = d2f==0
d2f[bad] = 1e-10
cor = df / d2f
print((abs(cor)>1).sum())
cor[abs(cor)>1] = 0
cor[bad] = 0
got = numpy.interp(peaks-cor[peaks],
numpy.arange(len(integrate_result.radial)),
integrate_result.radial)
mask = numpy.logical_and(got>=tth_min,
got<=tth_max)
got = got[mask]
target = numpy.array(calibrant.get_2th())*integrate_result.unit.scale
mask = numpy.logical_and(target>=tth_min,
target<=tth_max)
target = target[mask]
print(len(got), len(target))
d2 = distance_matrix(target.reshape(-1, 1 ),
got.reshape(-1, 1), p=1)
return target, target-got[d2.argmin(axis=-1)]
[24]:
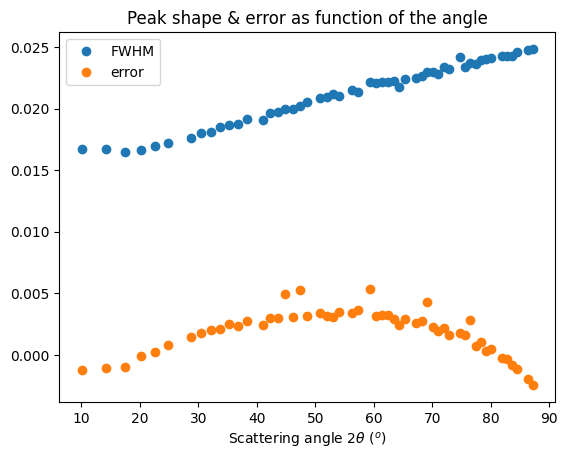
fig, ax = plt.subplots()
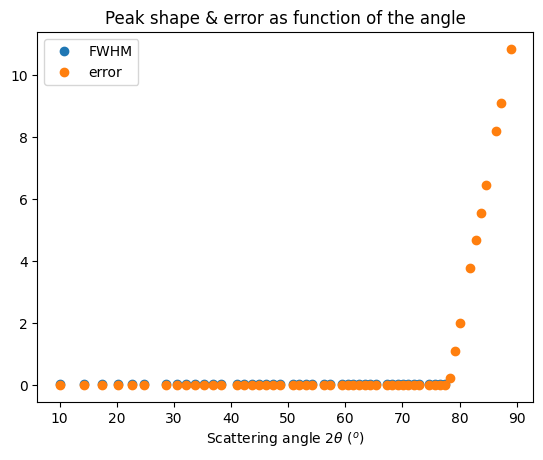
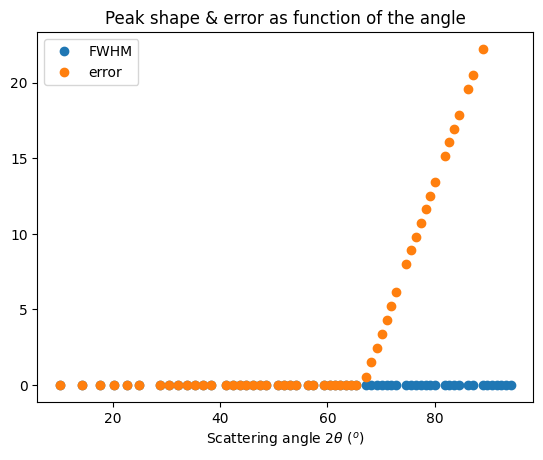
ax.plot(*calc_fwhm(res_mg, LaB6_new), "o", label="FWHM")
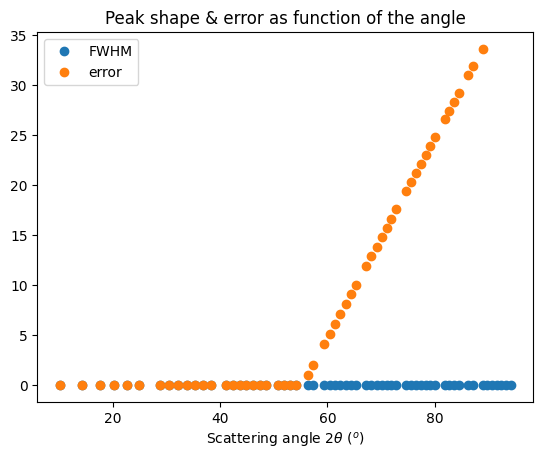
ax.plot(*calc_peak_error(res_mg, LaB6_new), "o", label="offset")
ax.set_title("Peak shape & error as function of the angle")
ax.set_xlabel(res_mg.unit.label)
ax.legend()
fig.show()
29218
81 60
/tmp/ipykernel_367778/55614379.py:7: UserWarning: Matplotlib is currently using module://matplotlib_inline.backend_inline, which is a non-GUI backend, so cannot show the figure.
fig.show()
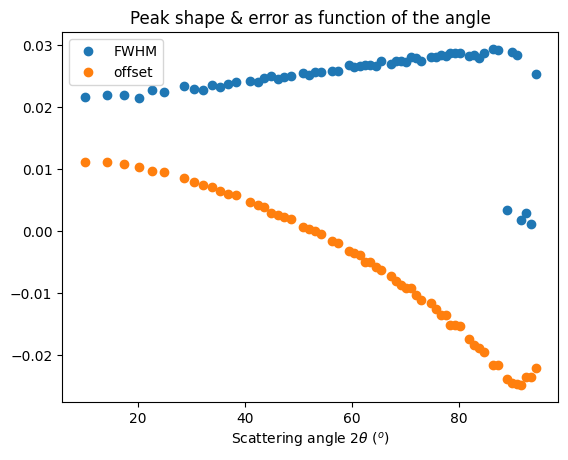
Module 1
We can apply the same procdure for the second module … and try to rationalize the procedure.
[25]:
module_id = 1
name = ds_names[module_id]
ds = data[name]
zero_pos = 64
frame_start = 103
frame_stop = 123
[26]:
param1 = {"dist": 0.72,
"poni1": 640*50e-6,
"poni2": 4e-3,
"rot1":0,
"offset": -get_position(zero_pos),
"scale":1,
"nrj": nrj}
#Lock enegy for now and a couple of other parameters
bounds1 = {"nrj": (nrj, nrj),
"dist": (0.7, 0.8),
"poni2": (4e-3, 4e-3),
"rot1": (0,0),
"scale":(1,1), }
gonioref1 = GoniometerRefinement(param1,
get_position,
trans,
detector=modules[name],
wavelength=wl,
bounds=bounds1
)
print(gonioref1)
goniometers[name]=gonioref1
GoniometerRefinement with 0 geometries labeled: .
[27]:
#Exctract frames with peak#0
for i in range(frame_start, frame_stop):
cp = ControlPoints(calibrant=LaB6, wavelength=wl)
peak = peak_picking(name, i)
if len(peak)!=1:
continue
cp.append([peak[0]], ring=0)
img = (ds[i]).reshape((-1,1))
sg = gonioref1.new_geometry("%s_%04i"%(name,i),
image=img,
metadata=i,
control_points=cp,
calibrant=LaB6)
sg.geometry_refinement.data = numpy.array(cp.getList())
print(gonioref1)
print(gonioref1.chi2())
GoniometerRefinement with 20 geometries labeled: data_03_0103, data_03_0104, data_03_0105, data_03_0106, data_03_0107, data_03_0108, data_03_0109, data_03_0110, data_03_0111, data_03_0112, data_03_0113, data_03_0114, data_03_0115, data_03_0116, data_03_0117, data_03_0118, data_03_0119, data_03_0120, data_03_0121, data_03_0122.
1.4524664758918932e-06
[28]:
gonioref1.refine2()
Cost function before refinement: 1.4524664758918932e-06
[ 7.20000000e-01 3.20000000e-02 4.00000000e-03 0.00000000e+00
-7.72000000e+01 1.00000000e+00 1.70270825e+01]
message: Optimization terminated successfully
success: True
status: 0
fun: 2.343186420609047e-11
x: [ 7.200e-01 3.287e-02 4.000e-03 0.000e+00 -7.720e+01
1.000e+00 1.703e+01]
nit: 2
jac: [ 1.374e-07 1.035e-07 nan nan 9.897e-10
nan nan]
nfev: 9
njev: 2
Cost function after refinement: 2.343186420609047e-11
GonioParam(dist=0.7200063780235467, poni1=0.03286839545438533, poni2=0.004, rot1=0.0, offset=-77.19998908851593, scale=1.0, nrj=17.027082549190933)
maxdelta on: poni1 (1) 0.032 --> 0.03286839545438533
[28]:
array([ 7.20006378e-01, 3.28683955e-02, 4.00000000e-03, 0.00000000e+00,
-7.71999891e+01, 1.00000000e+00, 1.70270825e+01])
[29]:
#Exctract all frames with peak>0
tths = LaB6.get_2th()
#print(tths)
for i in range(frame_stop, ds.shape[0]):
frame_name = "%s_%04i"%(name, i)
if frame_name in gonioref1.single_geometries:
continue
peak = peak_picking(name, i)
ai=gonioref1.get_ai(get_position(i))
tth = ai.array_from_unit(unit="2th_rad", scale=False)
tth_low = tth[20]
tth_hi = tth[-20]
ttmin, ttmax = min(tth_low, tth_hi), max(tth_low, tth_hi)
valid_peaks = numpy.logical_and(ttmin<=tths, tths<ttmax)
cnt = valid_peaks.sum()
if (len(peak) == cnt) and cnt>0:
cp = ControlPoints(calibrant=LaB6, wavelength=wl)
#revert the order of assignment if needed !!
if tth_hi < tth_low:
peak = peak[-1::-1]
for p, r in zip(peak, numpy.where(valid_peaks)[0]):
cp.append([p], ring=r)
img = ds[i].reshape((-1,1))
sg = gonioref1.new_geometry(frame_name,
image=img,
metadata=i,
control_points=cp,
calibrant=LaB6)
sg.geometry_refinement.data = numpy.array(cp.getList())
#print(frame_name, len(sg.geometry_refinement.data))
print(" Number of peaks found and used for refinement")
print(sum([len(sg.geometry_refinement.data) for sg in gonioref1.single_geometries.values()]))
print("Residual error before fitting: ", gonioref1.chi2())
Number of peaks found and used for refinement
1183
Residual error before fitting: 6.334637850688808e-07
[30]:
gonioref1.refine2()
gonioref1.set_bounds("poni1", -1, 1)
gonioref1.set_bounds("poni2", -1, 1)
gonioref1.set_bounds("rot1", -1, 1)
gonioref1.set_bounds("scale", 0.9, 1.1)
gonioref1.refine2()
Cost function before refinement: 6.334637850688808e-07
[ 7.20006378e-01 3.28683955e-02 4.00000000e-03 0.00000000e+00
-7.71999891e+01 1.00000000e+00 1.70270825e+01]
message: Optimization terminated successfully
success: True
status: 0
fun: 1.3797258269094543e-07
x: [ 7.200e-01 3.338e-02 4.000e-03 0.000e+00 -7.720e+01
1.000e+00 1.703e+01]
nit: 2
jac: [-4.626e-07 2.408e-08 nan nan 1.330e-11
nan nan]
nfev: 9
njev: 2
Cost function after refinement: 1.3797258269094543e-07
GonioParam(dist=0.7200063394925221, poni1=0.033375469748006405, poni2=0.004, rot1=0.0, offset=-77.1999827124022, scale=1.0, nrj=17.027082549190933)
maxdelta on: poni1 (1) 0.03286839545438533 --> 0.033375469748006405
Cost function before refinement: 1.3797258269094543e-07
[ 7.20006339e-01 3.33754697e-02 4.00000000e-03 0.00000000e+00
-7.71999827e+01 1.00000000e+00 1.70270825e+01]
message: Optimization terminated successfully
success: True
status: 0
fun: 8.828503235714087e-10
x: [ 7.207e-01 3.368e-02 4.058e-03 -4.449e-05 -7.720e+01
9.990e-01 1.703e+01]
nit: 13
jac: [ 6.561e-08 6.554e-07 -1.755e-07 1.262e-07 7.935e-09
2.914e-07 nan]
nfev: 91
njev: 13
Cost function after refinement: 8.828503235714087e-10
GonioParam(dist=0.720682072663415, poni1=0.03367823301601242, poni2=0.004058010685114263, rot1=-4.448556851210191e-05, offset=-77.19997879322797, scale=0.9989672333399332, nrj=17.027082549190933)
maxdelta on: scale (5) 1.0 --> 0.9989672333399332
[30]:
array([ 7.20682073e-01, 3.36782330e-02, 4.05801069e-03, -4.44855685e-05,
-7.71999788e+01, 9.98967233e-01, 1.70270825e+01])
[31]:
mg1 = gonioref1.get_mg(position)
mg1.radial_range = (0, 95)
images = [i.reshape(-1, 1) for i in data[name]]
res_mg1 = mg1.integrate1d(images, 50000)
results[name] = res_mg1
[32]:
LaB6_new = get_calibrant("LaB6")
LaB6_new.wavelength = hc/gonioref1.param[-1]*1e-10
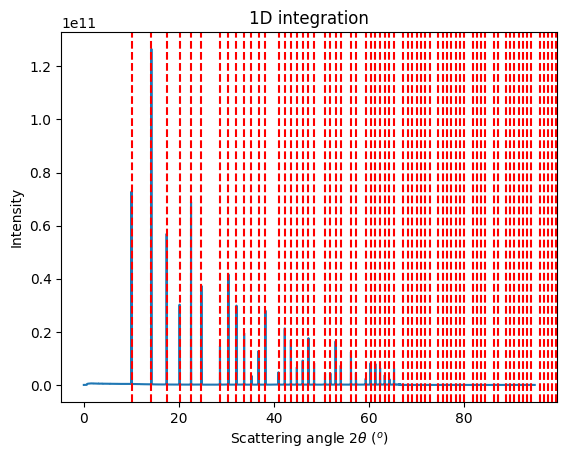
p = jupyter.plot1d(res_mg1, calibrant=LaB6_new)
p.figure.show()
/tmp/ipykernel_367778/3210620731.py:4: UserWarning: Matplotlib is currently using module://matplotlib_inline.backend_inline, which is a non-GUI backend, so cannot show the figure.
p.figure.show()
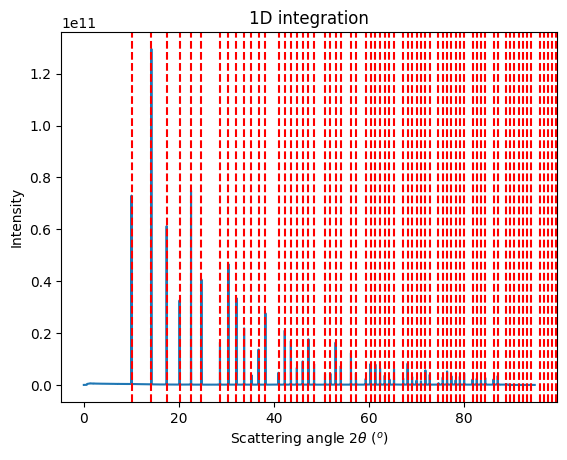
[33]:
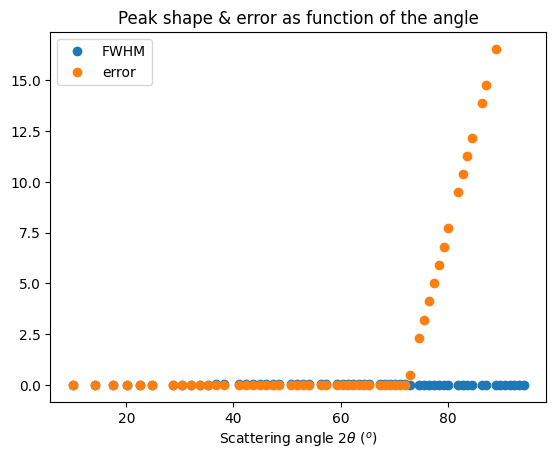
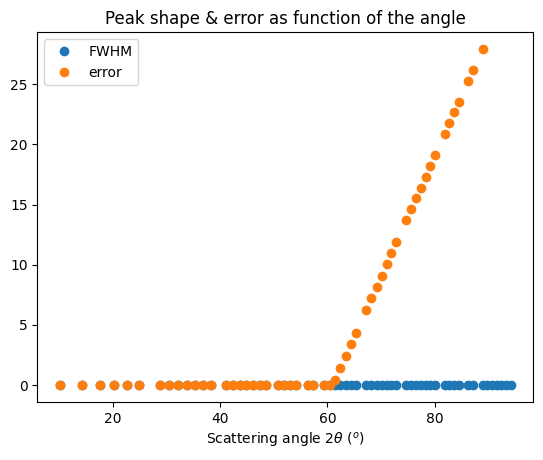
fig, ax = plt.subplots()
ax.plot(*calc_fwhm(res_mg1, LaB6_new, 10, 88), "o", label="FWHM")
ax.plot(*calc_peak_error(res_mg1, LaB6_new, 10, 88), "o", label="error")
ax.set_title("Peak shape & error as function of the angle")
ax.set_xlabel(res_mg.unit.label)
ax.legend()
fig.show()
27712
72 53
/tmp/ipykernel_367778/2659044189.py:7: UserWarning: Matplotlib is currently using module://matplotlib_inline.backend_inline, which is a non-GUI backend, so cannot show the figure.
fig.show()
All other Modules
We define now an automatic procedure for any module. The detection used 3 parameter visually extracted from the Figure1:
zero_pos: the frame where the beam-stop is in the center of the module
frame_start: the frame where the first peak of LaB6 appears (positive)
frame_stop: the frame where the second peak of LaB6 appears (positive)
This is enough for boot-strapping the goniometer configuration.
[34]:
def add_module(name,
zero_pos,
frame_start,
frame_stop,
):
ds = data[name]
param = {"dist": 0.72,
"poni1": 640*50e-6,
"poni2": 4e-3,
"rot1":0,
"offset": -get_position(zero_pos),
"scale":1,
"nrj": nrj}
#Lock enegy for now and a couple of other parameters
bounds = {"nrj": (nrj, nrj),
"dist": (0.7, 0.8),
"poni2": (4e-3, 4e-3),
"rot1": (0,0),
"scale": (1,1)}
gonioref = GoniometerRefinement(param,
get_position,
trans,
detector=modules[name],
wavelength=wl,
bounds=bounds
)
goniometers[name] = gonioref
for i in range(frame_start, frame_stop):
cp = ControlPoints(calibrant=LaB6, wavelength=wl)
peak = peak_picking(name, i)
if len(peak)!=1:
continue
cp.append([peak[0]], ring=0)
img = (ds[i]).reshape((-1,1))
sg = gonioref.new_geometry("%s_%04i"%(name, i),
image=img,
metadata=i,
control_points=cp,
calibrant=LaB6)
sg.geometry_refinement.data = numpy.array(cp.getList())
print(gonioref.chi2())
gonioref.refine2()
tths = LaB6.get_2th()
#print(tths)
for i in range(frame_stop, ds.shape[0]):
frame_name = "%s_%04i"%(name, i)
if frame_name in gonioref.single_geometries:
continue
peak = peak_picking(name, i)
ai=gonioref.get_ai(get_position(i))
tth = ai.array_from_unit(unit="2th_rad", scale=False)
tth_low = tth[20]
tth_hi = tth[-20]
ttmin, ttmax = min(tth_low, tth_hi), max(tth_low, tth_hi)
valid_peaks = numpy.logical_and(ttmin<=tths, tths<ttmax)
cnt = valid_peaks.sum()
if (len(peak) == cnt) and cnt>0:
cp = ControlPoints(calibrant=LaB6, wavelength=wl)
#revert the order of assignment if needed !!
if tth_hi < tth_low:
peak = peak[-1::-1]
for p, r in zip(peak, numpy.where(valid_peaks)[0]):
cp.append([p], ring=r)
img = (ds[i]).reshape((-1,1))
sg = gonioref.new_geometry(frame_name,
image=img,
metadata=i,
control_points=cp,
calibrant=LaB6)
sg.geometry_refinement.data = numpy.array(cp.getList())
#print(frame_name, len(sg.geometry_refinement.data))
print(" Number of peaks found and used for refinement")
print(sum([len(sg.geometry_refinement.data) for sg in gonioref.single_geometries.values()]))
gonioref.refine2()
gonioref.set_bounds("poni1", -1, 1)
gonioref.set_bounds("poni2", -1, 1)
gonioref.set_bounds("rot1", -1, 1)
gonioref.set_bounds("scale", 0.9, 1.1)
gonioref.refine2()
mg = gonioref.get_mg(position)
mg.radial_range = (0, 95)
images = [i.reshape(-1, 1) for i in ds]
res_mg = mg.integrate1d(images, 50000)
results[name] = res_mg
LaB6_new = get_calibrant("LaB6")
LaB6_new.wavelength = hc/gonioref.param[-1]*1e-10
p = jupyter.plot1d(res_mg, calibrant=LaB6_new)
p.figure.show()
fig, ax = plt.subplots()
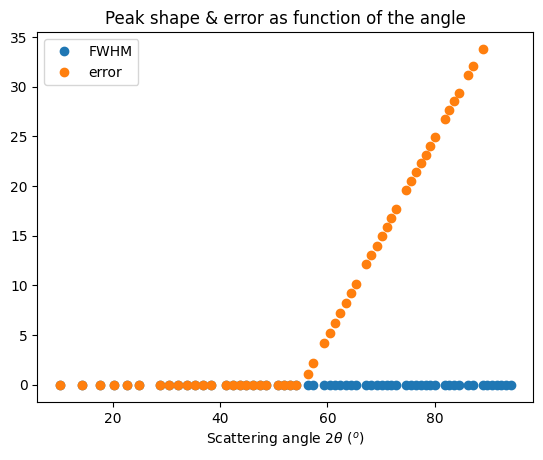
ax.plot(*calc_fwhm(res_mg, LaB6_new), "o", label="FWHM")
ax.plot(*calc_peak_error(res_mg, LaB6_new, 10, 89), "o", label="error")
ax.set_title("Peak shape & error as function of the angle")
ax.set_xlabel(res_mg.unit.label)
ax.legend()
fig.show()
[35]:
add_module(ds_names[2],
92,
131,
151)
8.40633024472856e-06
Cost function before refinement: 8.40633024472856e-06
[ 7.20000000e-01 3.20000000e-02 4.00000000e-03 0.00000000e+00
-7.15999445e+01 1.00000000e+00 1.70270825e+01]
message: Optimization terminated successfully
success: True
status: 0
fun: 1.8085719501136514e-11
x: [ 7.200e-01 3.409e-02 4.000e-03 0.000e+00 -7.160e+01
1.000e+00 1.703e+01]
nit: 2
jac: [ 4.574e-08 8.170e-07 nan nan 9.916e-09
nan nan]
nfev: 9
njev: 2
Cost function after refinement: 1.8085719501136514e-11
GonioParam(dist=0.7200189604924729, poni1=0.034089307266644636, poni2=0.004, rot1=0.0, offset=-71.59991818231154, scale=1.0, nrj=17.027082549190933)
maxdelta on: poni1 (1) 0.032 --> 0.034089307266644636
Number of peaks found and used for refinement
1093
Cost function before refinement: 5.557202432497131e-07
[ 7.20018960e-01 3.40893073e-02 4.00000000e-03 0.00000000e+00
-7.15999182e+01 1.00000000e+00 1.70270825e+01]
message: Optimization terminated successfully
success: True
status: 0
fun: 1.1960984572759293e-07
x: [ 7.200e-01 3.457e-02 4.000e-03 0.000e+00 -7.160e+01
1.000e+00 1.703e+01]
nit: 2
jac: [-9.442e-07 2.309e-08 nan nan -1.668e-11
nan nan]
nfev: 9
njev: 2
Cost function after refinement: 1.1960984572759293e-07
GonioParam(dist=0.7200183446946246, poni1=0.03456504217138479, poni2=0.004, rot1=0.0, offset=-71.5999122000852, scale=1.0, nrj=17.027082549190933)
maxdelta on: poni1 (1) 0.034089307266644636 --> 0.03456504217138479
Cost function before refinement: 1.1960984572759293e-07
[ 7.20018345e-01 3.45650422e-02 4.00000000e-03 0.00000000e+00
-7.15999122e+01 1.00000000e+00 1.70270825e+01]
message: Optimization terminated successfully
success: True
status: 0
fun: 6.570414650006303e-10
x: [ 7.207e-01 3.482e-02 4.043e-03 -3.377e-05 -7.160e+01
9.990e-01 1.703e+01]
nit: 10
jac: [ 2.182e-08 1.739e-08 -1.608e-07 1.158e-07 -1.824e-10
8.080e-09 nan]
nfev: 70
njev: 10
Cost function after refinement: 6.570414650006303e-10
GonioParam(dist=0.7206864291588817, poni1=0.03482474083006927, poni2=0.004043166284269385, rot1=-3.376838364866449e-05, offset=-71.59990881341272, scale=0.9989828730379465, nrj=17.027082549190933)
maxdelta on: scale (5) 1.0 --> 0.9989828730379465
/tmp/ipykernel_367778/465879643.py:99: UserWarning: Matplotlib is currently using module://matplotlib_inline.backend_inline, which is a non-GUI backend, so cannot show the figure.
p.figure.show()
25659
71 54
/tmp/ipykernel_367778/465879643.py:107: UserWarning: Matplotlib is currently using module://matplotlib_inline.backend_inline, which is a non-GUI backend, so cannot show the figure.
fig.show()
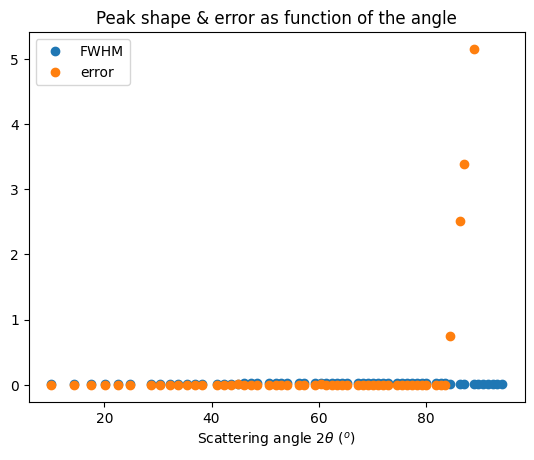
[36]:
add_module(ds_names[3],
121,
159,
179)
1.0825377842185958e-06
Cost function before refinement: 1.0825377842185958e-06
[ 7.20000000e-01 3.20000000e-02 4.00000000e-03 0.00000000e+00
-6.57999444e+01 1.00000000e+00 1.70270825e+01]
message: Optimization terminated successfully
success: True
status: 0
fun: 2.4921937668954493e-11
x: [ 7.200e-01 3.275e-02 4.000e-03 0.000e+00 -6.580e+01
1.000e+00 1.703e+01]
nit: 2
jac: [-8.600e-08 7.994e-08 nan nan 6.189e-10
nan nan]
nfev: 9
njev: 2
Cost function after refinement: 2.4921937668954493e-11
GonioParam(dist=0.7200067449756247, poni1=0.03274966118487238, poni2=0.004, rot1=0.0, offset=-65.7999350248995, scale=1.0, nrj=17.027082549190933)
maxdelta on: poni1 (1) 0.032 --> 0.03274966118487238
Number of peaks found and used for refinement
978
Cost function before refinement: 4.7051020473788555e-07
[ 7.20006745e-01 3.27496612e-02 4.00000000e-03 0.00000000e+00
-6.57999350e+01 1.00000000e+00 1.70270825e+01]
message: Optimization terminated successfully
success: True
status: 0
fun: 9.923942799031425e-08
x: [ 7.205e-01 3.319e-02 4.000e-03 0.000e+00 -6.580e+01
1.000e+00 1.703e+01]
nit: 7
jac: [-1.340e-09 -8.952e-12 nan nan -3.955e-10
nan nan]
nfev: 29
njev: 7
Cost function after refinement: 9.923942799031425e-08
GonioParam(dist=0.7204818161545966, poni1=0.033188632482365366, poni2=0.004, rot1=0.0, offset=-65.79992934723474, scale=1.0, nrj=17.027082549190933)
maxdelta on: dist (0) 0.7200067449756247 --> 0.7204818161545966
Cost function before refinement: 9.923942799031425e-08
[ 7.20481816e-01 3.31886325e-02 4.00000000e-03 0.00000000e+00
-6.57999293e+01 1.00000000e+00 1.70270825e+01]
message: Optimization terminated successfully
success: True
status: 0
fun: 5.124871954470427e-10
x: [ 7.205e-01 3.341e-02 3.978e-03 1.591e-05 -6.580e+01
9.990e-01 1.703e+01]
nit: 5
jac: [-5.053e-07 -5.371e-09 -1.298e-07 9.555e-08 -4.364e-10
2.566e-09 nan]
nfev: 36
njev: 5
Cost function after refinement: 5.124871954470427e-10
GonioParam(dist=0.7204829253887527, poni1=0.03340994866191066, poni2=0.003977911642428385, rot1=1.5909827962256308e-05, offset=-65.79992655958921, scale=0.9989991199293132, nrj=17.027082549190933)
maxdelta on: scale (5) 1.0 --> 0.9989991199293132
/tmp/ipykernel_367778/465879643.py:99: UserWarning: Matplotlib is currently using module://matplotlib_inline.backend_inline, which is a non-GUI backend, so cannot show the figure.
p.figure.show()
24026
64 54
/tmp/ipykernel_367778/465879643.py:107: UserWarning: Matplotlib is currently using module://matplotlib_inline.backend_inline, which is a non-GUI backend, so cannot show the figure.
fig.show()
[37]:
add_module(ds_names[4],
150,
188,
208)
2.3193001243857842e-07
Cost function before refinement: 2.3193001243857842e-07
[ 7.20000000e-01 3.20000000e-02 4.00000000e-03 0.00000000e+00
-6.00000556e+01 1.00000000e+00 1.70270825e+01]
message: Optimization terminated successfully
success: True
status: 0
fun: 2.085662476197838e-10
x: [ 7.200e-01 3.165e-02 4.000e-03 0.000e+00 -6.000e+01
1.000e+00 1.703e+01]
nit: 2
jac: [-2.720e-07 2.346e-08 nan nan -9.145e-11
nan nan]
nfev: 9
njev: 2
Cost function after refinement: 2.085662476197838e-10
GonioParam(dist=0.7199968842266145, poni1=0.03165314623342505, poni2=0.004, rot1=0.0, offset=-60.00005992107673, scale=1.0, nrj=17.027082549190933)
maxdelta on: poni1 (1) 0.032 --> 0.03165314623342505
Number of peaks found and used for refinement
864
Cost function before refinement: 3.8832764505567803e-07
[ 7.19996884e-01 3.16531462e-02 4.00000000e-03 0.00000000e+00
-6.00000599e+01 1.00000000e+00 1.70270825e+01]
message: Optimization terminated successfully
success: True
status: 0
fun: 8.355695005974523e-08
x: [ 7.206e-01 3.205e-02 4.000e-03 0.000e+00 -6.000e+01
1.000e+00 1.703e+01]
nit: 7
jac: [-2.493e-09 -1.943e-11 nan nan -2.948e-10
nan nan]
nfev: 29
njev: 7
Cost function after refinement: 8.355695005974523e-08
GonioParam(dist=0.7206442268536376, poni1=0.03204960860571386, poni2=0.004, rot1=0.0, offset=-60.0000548000565, scale=1.0, nrj=17.027082549190933)
maxdelta on: dist (0) 0.7199968842266145 --> 0.7206442268536376
Cost function before refinement: 8.355695005974523e-08
[ 7.20644227e-01 3.20496086e-02 4.00000000e-03 0.00000000e+00
-6.00000548e+01 1.00000000e+00 1.70270825e+01]
message: Optimization terminated successfully
success: True
status: 0
fun: 3.338833374910402e-10
x: [ 7.206e-01 3.224e-02 3.976e-03 1.754e-05 -6.000e+01
9.990e-01 1.703e+01]
nit: 5
jac: [-3.349e-07 -1.351e-09 -1.135e-07 8.314e-08 -3.434e-10
3.682e-09 nan]
nfev: 36
njev: 5
Cost function after refinement: 3.338833374910402e-10
GonioParam(dist=0.7206453081721997, poni1=0.03223711680104726, poni2=0.0039756515739672454, rot1=1.7542241829967905e-05, offset=-60.00005243766022, scale=0.9990118655636463, nrj=17.027082549190933)
maxdelta on: scale (5) 1.0 --> 0.9990118655636463
/tmp/ipykernel_367778/465879643.py:99: UserWarning: Matplotlib is currently using module://matplotlib_inline.backend_inline, which is a non-GUI backend, so cannot show the figure.
p.figure.show()
22251
56 54
/tmp/ipykernel_367778/465879643.py:107: UserWarning: Matplotlib is currently using module://matplotlib_inline.backend_inline, which is a non-GUI backend, so cannot show the figure.
fig.show()
[38]:
add_module(ds_names[5],
178,
216,
236)
1.4965819410817478e-06
Cost function before refinement: 1.4965819410817478e-06
[ 7.20000000e-01 3.20000000e-02 4.00000000e-03 0.00000000e+00
-5.43998333e+01 1.00000000e+00 1.70270825e+01]
message: Optimization terminated successfully
success: True
status: 0
fun: 2.0171535049901094e-10
x: [ 7.200e-01 3.288e-02 4.000e-03 0.000e+00 -5.440e+01
1.000e+00 1.703e+01]
nit: 2
jac: [-2.790e-07 1.127e-07 nan nan 1.017e-09
nan nan]
nfev: 9
njev: 2
Cost function after refinement: 2.0171535049901094e-10
GonioParam(dist=0.7200081377942467, poni1=0.03288139794526324, poni2=0.004, rot1=0.0, offset=-54.39982225664511, scale=1.0, nrj=17.027082549190933)
maxdelta on: poni1 (1) 0.032 --> 0.03288139794526324
Number of peaks found and used for refinement
754
Cost function before refinement: 3.084364539629558e-07
[ 7.20008138e-01 3.28813979e-02 4.00000000e-03 0.00000000e+00
-5.43998223e+01 1.00000000e+00 1.70270825e+01]
message: Optimization terminated successfully
success: True
status: 0
fun: 6.550962572089796e-08
x: [ 7.205e-01 3.324e-02 4.000e-03 0.000e+00 -5.440e+01
1.000e+00 1.703e+01]
nit: 7
jac: [-1.598e-09 -1.620e-11 nan nan -3.332e-10
nan nan]
nfev: 29
njev: 7
Cost function after refinement: 6.550962572089796e-08
GonioParam(dist=0.7205268320603014, poni1=0.03323636624652024, poni2=0.004, rot1=0.0, offset=-54.399817662277066, scale=1.0, nrj=17.027082549190933)
maxdelta on: dist (0) 0.7200081377942467 --> 0.7205268320603014
Cost function before refinement: 6.550962572089796e-08
[ 7.20526832e-01 3.32363662e-02 4.00000000e-03 0.00000000e+00
-5.43998177e+01 1.00000000e+00 1.70270825e+01]
message: Optimization terminated successfully
success: True
status: 0
fun: 2.980133018674163e-10
x: [ 7.205e-01 3.339e-02 3.973e-03 1.948e-05 -5.440e+01
9.990e-01 1.703e+01]
nit: 5
jac: [-6.288e-07 -6.165e-09 -8.418e-08 6.319e-08 -4.255e-10
1.871e-09 nan]
nfev: 36
njev: 5
Cost function after refinement: 2.980133018674163e-10
GonioParam(dist=0.7205282661392393, poni1=0.03339481351901525, poni2=0.003972951169717649, rot1=1.9483670504509448e-05, offset=-54.39981566521699, scale=0.9990259510567647, nrj=17.027082549190933)
maxdelta on: scale (5) 1.0 --> 0.9990259510567647
/tmp/ipykernel_367778/465879643.py:99: UserWarning: Matplotlib is currently using module://matplotlib_inline.backend_inline, which is a non-GUI backend, so cannot show the figure.
p.figure.show()
20549
54 54
/tmp/ipykernel_367778/465879643.py:107: UserWarning: Matplotlib is currently using module://matplotlib_inline.backend_inline, which is a non-GUI backend, so cannot show the figure.
fig.show()
[39]:
add_module(ds_names[6],
207,
245,
266)
7.41484379835199e-08
Cost function before refinement: 7.41484379835199e-08
[ 7.20000000e-01 3.20000000e-02 4.00000000e-03 0.00000000e+00
-4.85998889e+01 1.00000000e+00 1.70270825e+01]
message: Optimization terminated successfully
success: True
status: 0
fun: 5.651340369404608e-11
x: [ 7.200e-01 3.180e-02 4.000e-03 0.000e+00 -4.860e+01
1.000e+00 1.703e+01]
nit: 2
jac: [-2.813e-07 1.905e-08 nan nan -1.234e-10
nan nan]
nfev: 9
njev: 2
Cost function after refinement: 5.651340369404608e-11
GonioParam(dist=0.7199985717445607, poni1=0.03180385768846998, poni2=0.004, rot1=0.0, offset=-48.599891358723, scale=1.0, nrj=17.027082549190933)
maxdelta on: poni1 (1) 0.032 --> 0.03180385768846998
Number of peaks found and used for refinement
626
Cost function before refinement: 2.383303034849477e-07
[ 7.19998572e-01 3.18038577e-02 4.00000000e-03 0.00000000e+00
-4.85998914e+01 1.00000000e+00 1.70270825e+01]
message: Optimization terminated successfully
success: True
status: 0
fun: 5.1983308105299717e-08
x: [ 7.206e-01 3.211e-02 4.000e-03 0.000e+00 -4.860e+01
1.000e+00 1.703e+01]
nit: 7
jac: [-2.199e-09 -2.335e-11 nan nan -2.599e-10
nan nan]
nfev: 29
njev: 7
Cost function after refinement: 5.1983308105299717e-08
GonioParam(dist=0.7206068542793277, poni1=0.03211384891528438, poni2=0.004, rot1=0.0, offset=-48.599887342572686, scale=1.0, nrj=17.027082549190933)
maxdelta on: dist (0) 0.7199985717445607 --> 0.7206068542793277
Cost function before refinement: 5.1983308105299717e-08
[ 7.20606854e-01 3.21138489e-02 4.00000000e-03 0.00000000e+00
-4.85998873e+01 1.00000000e+00 1.70270825e+01]
message: Optimization terminated successfully
success: True
status: 0
fun: 2.556084121448774e-10
x: [ 7.206e-01 3.225e-02 3.969e-03 2.238e-05 -4.860e+01
9.990e-01 1.703e+01]
nit: 6
jac: [-6.637e-07 8.690e-08 -6.746e-08 5.130e-08 7.875e-10
2.881e-09 nan]
nfev: 42
njev: 6
Cost function after refinement: 2.556084121448774e-10
GonioParam(dist=0.7206092934239683, poni1=0.03224725723057559, poni2=0.003968935506155581, rot1=2.237548771450148e-05, offset=-48.59988566030428, scale=0.9990409081096999, nrj=17.027082549190933)
maxdelta on: scale (5) 1.0 --> 0.9990409081096999
/tmp/ipykernel_367778/465879643.py:99: UserWarning: Matplotlib is currently using module://matplotlib_inline.backend_inline, which is a non-GUI backend, so cannot show the figure.
p.figure.show()
18650
54 54
/tmp/ipykernel_367778/465879643.py:107: UserWarning: Matplotlib is currently using module://matplotlib_inline.backend_inline, which is a non-GUI backend, so cannot show the figure.
fig.show()
[40]:
add_module(ds_names[7],
236,
273,
293)
4.377487894658635e-06
Cost function before refinement: 4.377487894658635e-06
[ 7.20000000e-01 3.20000000e-02 4.00000000e-03 0.00000000e+00
-4.27998889e+01 1.00000000e+00 1.70270825e+01]
message: Optimization terminated successfully
success: True
status: 0
fun: 9.109058146293743e-11
x: [ 7.200e-01 3.049e-02 4.000e-03 0.000e+00 -4.280e+01
1.000e+00 1.703e+01]
nit: 2
jac: [-3.538e-07 3.502e-09 nan nan -3.652e-10
nan nan]
nfev: 9
njev: 2
Cost function after refinement: 9.109058146293743e-11
GonioParam(dist=0.7199860337927957, poni1=0.030492505461750096, poni2=0.004, rot1=0.0, offset=-42.79990784449265, scale=1.0, nrj=17.027082549190933)
maxdelta on: poni1 (1) 0.032 --> 0.030492505461750096
Number of peaks found and used for refinement
543
Cost function before refinement: 1.911534453472336e-07
[ 7.19986034e-01 3.04925055e-02 4.00000000e-03 0.00000000e+00
-4.27999078e+01 1.00000000e+00 1.70270825e+01]
message: Optimization terminated successfully
success: True
status: 0
fun: 4.121300333570348e-08
x: [ 7.207e-01 3.077e-02 4.000e-03 0.000e+00 -4.280e+01
1.000e+00 1.703e+01]
nit: 7
jac: [-3.061e-09 -2.322e-11 nan nan -3.626e-10
nan nan]
nfev: 29
njev: 7
Cost function after refinement: 4.121300333570348e-08
GonioParam(dist=0.720705554602103, poni1=0.03076843090598898, poni2=0.004, rot1=0.0, offset=-42.799904173872896, scale=1.0, nrj=17.027082549190933)
maxdelta on: dist (0) 0.7199860337927957 --> 0.720705554602103
Cost function before refinement: 4.121300333570348e-08
[ 7.20705555e-01 3.07684309e-02 4.00000000e-03 0.00000000e+00
-4.27999042e+01 1.00000000e+00 1.70270825e+01]
message: Optimization terminated successfully
success: True
status: 0
fun: 1.905573974207547e-10
x: [ 7.207e-01 3.086e-02 3.965e-03 2.507e-05 -4.280e+01
9.991e-01 1.703e+01]
nit: 5
jac: [-5.207e-07 -3.451e-07 -5.785e-08 4.380e-08 -4.683e-09
9.352e-08 nan]
nfev: 35
njev: 5
Cost function after refinement: 1.905573974207547e-10
GonioParam(dist=0.7207071581128385, poni1=0.030863392388519827, poni2=0.003965206217913014, rot1=2.5069661472187673e-05, offset=-42.799902973828175, scale=0.9990506059528655, nrj=17.027082549190933)
maxdelta on: scale (5) 1.0 --> 0.9990506059528655
/tmp/ipykernel_367778/465879643.py:99: UserWarning: Matplotlib is currently using module://matplotlib_inline.backend_inline, which is a non-GUI backend, so cannot show the figure.
p.figure.show()
16803
45 54
/tmp/ipykernel_367778/465879643.py:107: UserWarning: Matplotlib is currently using module://matplotlib_inline.backend_inline, which is a non-GUI backend, so cannot show the figure.
fig.show()
[41]:
add_module(ds_names[8],
264,
302,
322)
9.734136493812279e-08
Cost function before refinement: 9.734136493812279e-08
[ 7.20000000e-01 3.20000000e-02 4.00000000e-03 0.00000000e+00
-3.72000000e+01 1.00000000e+00 1.70270825e+01]
message: Optimization terminated successfully
success: True
status: 0
fun: 1.383834659393779e-10
x: [ 7.200e-01 3.178e-02 4.000e-03 0.000e+00 -3.720e+01
1.000e+00 1.703e+01]
nit: 2
jac: [-5.987e-07 2.236e-08 nan nan -2.112e-10
nan nan]
nfev: 9
njev: 2
Cost function after refinement: 1.383834659393779e-10
GonioParam(dist=0.7199980533133431, poni1=0.0317753490052087, poni2=0.004, rot1=0.0, offset=-37.20000282728478, scale=1.0, nrj=17.027082549190933)
maxdelta on: poni1 (1) 0.032 --> 0.0317753490052087
Number of peaks found and used for refinement
454
Cost function before refinement: 1.4308139309115986e-07
[ 7.19998053e-01 3.17753490e-02 4.00000000e-03 0.00000000e+00
-3.72000028e+01 1.00000000e+00 1.70270825e+01]
message: Optimization terminated successfully
success: True
status: 0
fun: 3.226788268415189e-08
x: [ 7.208e-01 3.201e-02 4.000e-03 0.000e+00 -3.720e+01
1.000e+00 1.703e+01]
nit: 7
jac: [-3.925e-09 -5.222e-11 nan nan -3.043e-10
nan nan]
nfev: 29
njev: 7
Cost function after refinement: 3.226788268415189e-08
GonioParam(dist=0.7208093285809686, poni1=0.03201295264935034, poni2=0.004, rot1=0.0, offset=-37.19999969779676, scale=1.0, nrj=17.027082549190933)
maxdelta on: dist (0) 0.7199980533133431 --> 0.7208093285809686
Cost function before refinement: 3.226788268415189e-08
[ 7.20809329e-01 3.20129526e-02 4.00000000e-03 0.00000000e+00
-3.71999997e+01 1.00000000e+00 1.70270825e+01]
message: Optimization terminated successfully
success: True
status: 0
fun: 1.8511707669927584e-10
x: [ 7.208e-01 3.208e-02 3.960e-03 2.909e-05 -3.720e+01
9.991e-01 1.703e+01]
nit: 5
jac: [-5.574e-07 1.084e-09 -4.859e-08 3.728e-08 -3.498e-10
3.440e-09 nan]
nfev: 35
njev: 5
Cost function after refinement: 1.8511707669927584e-10
GonioParam(dist=0.720810786218182, poni1=0.0320817564491065, poni2=0.003959633634965548, rot1=2.9090593451096456e-05, offset=-37.199998826623414, scale=0.9990588539443465, nrj=17.027082549190933)
maxdelta on: scale (5) 1.0 --> 0.9990588539443465
/tmp/ipykernel_367778/465879643.py:99: UserWarning: Matplotlib is currently using module://matplotlib_inline.backend_inline, which is a non-GUI backend, so cannot show the figure.
p.figure.show()
16875
45 54
/tmp/ipykernel_367778/465879643.py:107: UserWarning: Matplotlib is currently using module://matplotlib_inline.backend_inline, which is a non-GUI backend, so cannot show the figure.
fig.show()
[42]:
len(goniometers)
[42]:
9
[43]:
# print all the parameters to be able to compare them visually
goniometers["data_12"] = goniometers["data_11"]
for name in ds_names:
print(name, *["%8.4e"%i for i in goniometers[name].param])
data_02 7.2310e-01 3.2054e-02 3.9849e-03 1.0948e-05 -8.2800e+01 9.9942e-01 1.7027e+01
data_03 7.2068e-01 3.3678e-02 4.0580e-03 -4.4486e-05 -7.7200e+01 9.9897e-01 1.7027e+01
data_04 7.2069e-01 3.4825e-02 4.0432e-03 -3.3768e-05 -7.1600e+01 9.9898e-01 1.7027e+01
data_05 7.2048e-01 3.3410e-02 3.9779e-03 1.5910e-05 -6.5800e+01 9.9900e-01 1.7027e+01
data_07 7.2065e-01 3.2237e-02 3.9757e-03 1.7542e-05 -6.0000e+01 9.9901e-01 1.7027e+01
data_08 7.2053e-01 3.3395e-02 3.9730e-03 1.9484e-05 -5.4400e+01 9.9903e-01 1.7027e+01
data_09 7.2061e-01 3.2247e-02 3.9689e-03 2.2375e-05 -4.8600e+01 9.9904e-01 1.7027e+01
data_10 7.2071e-01 3.0863e-02 3.9652e-03 2.5070e-05 -4.2800e+01 9.9905e-01 1.7027e+01
data_11 7.2081e-01 3.2082e-02 3.9596e-03 2.9091e-05 -3.7200e+01 9.9906e-01 1.7027e+01
data_12 7.2081e-01 3.2082e-02 3.9596e-03 2.9091e-05 -3.7200e+01 9.9906e-01 1.7027e+01
Use the negative part of the spectum …
Until now, we used only the data where 2th >0 For the last modules, this thows away half of the data.
We setup here a way to assign the peaks for the negative part of the spectrum.
[44]:
def complete_gonio(module_id=None, name=None):
"Scan missing frames for un-indexed peaks"
if name is None:
name = ds_names[module_id]
gonioref = goniometers[name]
ds = data[name]
print("Number of peaks previously found:",
sum([len(sg.geometry_refinement.data) for sg in gonioref.single_geometries.values()]))
tths = LaB6.get_2th()
for i in range(ds.shape[0]):
frame_name = "%s_%04i"%(name, i)
if frame_name in gonioref.single_geometries:
continue
peak = peak_picking(name, i)
ai=gonioref.get_ai(get_position(i))
tth = ai.array_from_unit(unit="2th_rad", scale=False)
tth_low = tth[20]
tth_hi = tth[-20]
ttmin, ttmax = min(tth_low, tth_hi), max(tth_low, tth_hi)
valid_peaks = numpy.logical_and(ttmin<=tths, tths<ttmax)
cnt = valid_peaks.sum()
if (len(peak) == cnt) and cnt>0:
cp = ControlPoints(calibrant=LaB6, wavelength=wl)
#revert the order of assignment if needed !!
if tth_hi < tth_low:
peak = peak[-1::-1]
for p, r in zip(peak, numpy.where(valid_peaks)[0]):
cp.append([p], ring=r)
img = ds[i].reshape((-1,1))
sg = gonioref.new_geometry(frame_name,
image=img,
metadata=i,
control_points=cp,
calibrant=LaB6)
sg.geometry_refinement.data = numpy.array(cp.getList())
#print(frame_name, len(sg.geometry_refinement.data))
print("Number of peaks found after re-scan:",
sum([len(sg.geometry_refinement.data) for sg in gonioref.single_geometries.values()]))
return gonioref
[45]:
gonio8 = complete_gonio(module_id=8)
gonio8.refine2()
Number of peaks previously found: 454
Number of peaks found after re-scan: 1006
Cost function before refinement: 4.707082320757526e-09
[ 7.20810786e-01 3.20817564e-02 3.95963363e-03 2.90905935e-05
-3.71999988e+01 9.99058854e-01 1.70270825e+01]
message: Optimization terminated successfully
success: True
status: 0
fun: 9.802713851439468e-10
x: [ 7.208e-01 3.208e-02 3.962e-03 2.771e-05 -3.720e+01
9.990e-01 1.703e+01]
nit: 4
jac: [-8.293e-07 1.798e-08 -2.226e-07 1.638e-07 -1.374e-10
-3.004e-08 nan]
nfev: 29
njev: 4
Cost function after refinement: 9.802713851439468e-10
GonioParam(dist=0.7208134358051861, poni1=0.03208491868712114, poni2=0.003961539924237118, rot1=2.7705794268123684e-05, offset=-37.19999878573076, scale=0.9989913574692074, nrj=17.027082549190933)
maxdelta on: scale (5) 0.9990588539443465 --> 0.9989913574692074
[45]:
array([ 7.20813436e-01, 3.20849187e-02, 3.96153992e-03, 2.77057943e-05,
-3.71999988e+01, 9.98991357e-01, 1.70270825e+01])
[46]:
gonio7 = complete_gonio(module_id=7)
Number of peaks previously found: 543
Number of peaks found after re-scan: 1004
[47]:
gonio7.refine2()
Cost function before refinement: 2.0497716259840994e-09
[ 7.20707158e-01 3.08633924e-02 3.96520622e-03 2.50696615e-05
-4.27999030e+01 9.99050606e-01 1.70270825e+01]
message: Optimization terminated successfully
success: True
status: 0
fun: 6.982166320635817e-10
x: [ 7.207e-01 3.087e-02 3.967e-03 2.399e-05 -4.280e+01
9.990e-01 1.703e+01]
nit: 4
jac: [-6.616e-07 1.821e-08 -2.311e-07 1.692e-07 -1.059e-10
-2.989e-08 nan]
nfev: 29
njev: 4
Cost function after refinement: 6.982166320635817e-10
GonioParam(dist=0.720709214422471, poni1=0.03086624488803945, poni2=0.003966690771283648, rot1=2.39914176175178e-05, offset=-42.799902936946246, scale=0.9990066875067236, nrj=17.027082549190933)
maxdelta on: scale (5) 0.9990506059528655 --> 0.9990066875067236
[47]:
array([ 7.20709214e-01, 3.08662449e-02, 3.96669077e-03, 2.39914176e-05,
-4.27999029e+01, 9.99006688e-01, 1.70270825e+01])
[48]:
gonio6 = complete_gonio(module_id=6)
gonio6.refine2()
Number of peaks previously found: 626
Number of peaks found after re-scan: 990
Cost function before refinement: 9.054149840019781e-10
[ 7.20609293e-01 3.22472572e-02 3.96893551e-03 2.23754877e-05
-4.85998857e+01 9.99040908e-01 1.70270825e+01]
message: Optimization terminated successfully
success: True
status: 0
fun: 6.093707047210183e-10
x: [ 7.206e-01 3.225e-02 3.970e-03 2.155e-05 -4.860e+01
9.990e-01 1.703e+01]
nit: 4
jac: [-8.022e-07 3.637e-08 -2.332e-07 1.713e-07 1.531e-10
-6.906e-08 nan]
nfev: 29
njev: 4
Cost function after refinement: 6.093707047210183e-10
GonioParam(dist=0.7206117522126192, poni1=0.03224903534974467, poni2=0.003970067520032141, rot1=2.154981768904857e-05, offset=-48.5998856370124, scale=0.999018042153128, nrj=17.027082549190933)
maxdelta on: scale (5) 0.9990409081096999 --> 0.999018042153128
[48]:
array([ 7.20611752e-01, 3.22490353e-02, 3.97006752e-03, 2.15498177e-05,
-4.85998856e+01, 9.99018042e-01, 1.70270825e+01])
[49]:
gonio5 = complete_gonio(module_id=5)
gonio5.refine2()
Number of peaks previously found: 754
Number of peaks found after re-scan: 1038
Cost function before refinement: 5.322293562205405e-10
[ 7.20528266e-01 3.33948135e-02 3.97295117e-03 1.94836705e-05
-5.43998157e+01 9.99025951e-01 1.70270825e+01]
message: Optimization terminated successfully
success: True
status: 0
fun: 5.247777068807799e-10
x: [ 7.205e-01 3.340e-02 3.974e-03 1.898e-05 -5.440e+01
9.990e-01 1.703e+01]
nit: 4
jac: [-6.548e-07 1.292e-07 -1.627e-07 1.198e-07 1.289e-09
-2.774e-07 nan]
nfev: 29
njev: 4
Cost function after refinement: 5.247777068807799e-10
GonioParam(dist=0.7205306818871419, poni1=0.03339533863359239, poni2=0.003973636919054829, rot1=1.8979820018941428e-05, offset=-54.39981565738007, scale=0.9990218992357166, nrj=17.027082549190933)
maxdelta on: scale (5) 0.9990259510567647 --> 0.9990218992357166
[49]:
array([ 7.20530682e-01, 3.33953386e-02, 3.97363692e-03, 1.89798200e-05,
-5.43998157e+01, 9.99021899e-01, 1.70270825e+01])
[50]:
gonio4 = complete_gonio(module_id=4)
gonio4.refine2()
Number of peaks previously found: 864
Number of peaks found after re-scan: 1081
Cost function before refinement: 4.522890520775561e-10
[ 7.20645308e-01 3.22371168e-02 3.97565157e-03 1.75422418e-05
-6.00000524e+01 9.99011866e-01 1.70270825e+01]
message: Optimization terminated successfully
success: True
status: 0
fun: 4.329909092681409e-10
x: [ 7.206e-01 3.224e-02 3.976e-03 1.742e-05 -6.000e+01
9.990e-01 1.703e+01]
nit: 4
jac: [-3.236e-07 -1.338e-08 -8.079e-08 5.953e-08 -4.927e-10
3.166e-08 nan]
nfev: 29
njev: 4
Cost function after refinement: 4.329909092681409e-10
GonioParam(dist=0.7206464175851856, poni1=0.032235988249254756, poni2=0.0039758195842887565, rot1=1.7416684299562826e-05, offset=-60.0000524507336, scale=0.9990197113116526, nrj=17.027082549190933)
maxdelta on: scale (5) 0.9990118655636463 --> 0.9990197113116526
[50]:
array([ 7.20646418e-01, 3.22359882e-02, 3.97581958e-03, 1.74166843e-05,
-6.00000525e+01, 9.99019711e-01, 1.70270825e+01])
[51]:
gonio3 = complete_gonio(module_id=3)
gonio3.refine2()
Number of peaks previously found: 978
Number of peaks found after re-scan: 1156
Cost function before refinement: 7.053066247292853e-10
[ 7.20482925e-01 3.34099487e-02 3.97791164e-03 1.59098280e-05
-6.57999266e+01 9.98999120e-01 1.70270825e+01]
message: Optimization terminated successfully
success: True
status: 0
fun: 6.316703213409536e-10
x: [ 7.205e-01 3.341e-02 3.978e-03 1.605e-05 -6.580e+01
9.990e-01 1.703e+01]
nit: 4
jac: [-4.998e-07 -1.632e-08 9.666e-09 -4.950e-09 -5.754e-10
3.901e-08 nan]
nfev: 29
njev: 4
Cost function after refinement: 6.316703213409536e-10
GonioParam(dist=0.7204847939312276, poni1=0.033407488249092, poni2=0.003977700789209715, rot1=1.605421293874649e-05, offset=-65.79992658915752, scale=0.9990156265501503, nrj=17.027082549190933)
maxdelta on: scale (5) 0.9989991199293132 --> 0.9990156265501503
[51]:
array([ 7.20484794e-01, 3.34074882e-02, 3.97770079e-03, 1.60542129e-05,
-6.57999266e+01, 9.99015627e-01, 1.70270825e+01])
[52]:
gonio2 = complete_gonio(module_id=2)
gonio2.refine2()
Number of peaks previously found: 1093
Number of peaks found after re-scan: 1229
Cost function before refinement: 8.306328970111712e-10
[ 7.20686429e-01 3.48247408e-02 4.04316628e-03 -3.37683836e-05
-7.15999088e+01 9.98982873e-01 1.70270825e+01]
message: Optimization terminated successfully
success: True
status: 0
fun: 7.771718764214187e-10
x: [ 7.207e-01 3.482e-02 4.043e-03 -3.357e-05 -7.160e+01
9.990e-01 1.703e+01]
nit: 4
jac: [ 9.152e-08 -1.052e-09 5.616e-08 -4.083e-08 -4.257e-10
2.851e-09 nan]
nfev: 29
njev: 4
Cost function after refinement: 7.771718764214187e-10
GonioParam(dist=0.7206860334374249, poni1=0.03482262187953887, poni2=0.004042896898550854, rot1=-3.357268964891843e-05, offset=-71.5999088383266, scale=0.9989982448525314, nrj=17.027082549190933)
maxdelta on: scale (5) 0.9989828730379465 --> 0.9989982448525314
[52]:
array([ 7.20686033e-01, 3.48226219e-02, 4.04289690e-03, -3.35726896e-05,
-7.15999088e+01, 9.98998245e-01, 1.70270825e+01])
[53]:
gonio1 = complete_gonio(module_id=1)
gonio1.refine2()
Number of peaks previously found: 1183
Number of peaks found after re-scan: 1285
Cost function before refinement: 9.822430107504146e-10
[ 7.20682073e-01 3.36782330e-02 4.05801069e-03 -4.44855685e-05
-7.71999788e+01 9.98967233e-01 1.70270825e+01]
message: Optimization terminated successfully
success: True
status: 0
fun: 9.683583561116745e-10
x: [ 7.207e-01 3.368e-02 4.058e-03 -4.454e-05 -7.720e+01
9.990e-01 1.703e+01]
nit: 4
jac: [ 1.052e-07 -1.409e-09 -2.647e-09 1.496e-09 -3.432e-10
4.363e-09 nan]
nfev: 29
njev: 4
Cost function after refinement: 9.683583561116745e-10
GonioParam(dist=0.7206815883863531, poni1=0.03367666939027231, poni2=0.004058082314538765, rot1=-4.453529530230961e-05, offset=-77.19997881135367, scale=0.9989759056428863, nrj=17.027082549190933)
maxdelta on: scale (5) 0.9989672333399332 --> 0.9989759056428863
[53]:
array([ 7.20681588e-01, 3.36766694e-02, 4.05808231e-03, -4.45352953e-05,
-7.71999788e+01, 9.98975906e-01, 1.70270825e+01])
[54]:
gonio0 = complete_gonio(module_id=0)
gonio0.refine2()
Number of peaks previously found: 1203
Number of peaks found after re-scan: 1255
Cost function before refinement: 2.580092915588822e-06
[ 7.23096244e-01 3.20537008e-02 3.98485488e-03 1.09477707e-05
-8.27999440e+01 9.99415058e-01 1.70270825e+01]
message: Optimization terminated successfully
success: True
status: 0
fun: 2.5799879786031964e-06
x: [ 7.231e-01 3.207e-02 3.981e-03 1.351e-05 -8.280e+01
9.994e-01 1.703e+01]
nit: 4
jac: [-1.439e-07 3.613e-08 5.528e-07 -3.992e-07 1.022e-09
-1.146e-07 nan]
nfev: 29
njev: 4
Cost function after refinement: 2.5799879786031964e-06
GonioParam(dist=0.7230969945154274, poni1=0.03206584438250582, poni2=0.003981302101258431, rot1=1.351375944293161e-05, offset=-82.79994383887343, scale=0.9993962397251773, nrj=17.027082549190933)
maxdelta on: scale (5) 0.9994150576486731 --> 0.9993962397251773
[54]:
array([ 7.23096995e-01, 3.20658444e-02, 3.98130210e-03, 1.35137594e-05,
-8.27999438e+01, 9.99396240e-01, 1.70270825e+01])
[55]:
#Rescan module0 which looks much different:
gonio0.single_geometries.clear()
gonio0 = complete_gonio(module_id=0)
gonio0.refine2()
Number of peaks previously found: 0
Number of peaks found after re-scan: 1250
Cost function before refinement: 9.454139650039214e-07
[ 7.23096995e-01 3.20658444e-02 3.98130210e-03 1.35137594e-05
-8.27999438e+01 9.99396240e-01 1.70270825e+01]
message: Optimization terminated successfully
success: True
status: 0
fun: 9.315197979050413e-07
x: [ 7.220e-01 3.220e-02 3.944e-03 4.514e-05 -8.280e+01
9.991e-01 1.703e+01]
nit: 9
jac: [-1.206e-08 -1.145e-08 1.037e-07 -7.484e-08 1.341e-10
-9.527e-09 nan]
nfev: 64
njev: 9
Cost function after refinement: 9.315197979050413e-07
GonioParam(dist=0.7219737518819529, poni1=0.032200315169332513, poni2=0.003943811455063223, rot1=4.514209223007649e-05, offset=-82.79994226212274, scale=0.9991407871114438, nrj=17.027082549190933)
maxdelta on: dist (0) 0.7230969945154274 --> 0.7219737518819529
[55]:
array([ 7.21973752e-01, 3.22003152e-02, 3.94381146e-03, 4.51420922e-05,
-8.27999423e+01, 9.99140787e-01, 1.70270825e+01])
Discard wronly assigned peaks
We have seen previously that some modules have a much higher residual error, while all have almost the same number of peaks recorded and fitted.
Some frames are contributing much more than all the other in those badly-fitted data. Let’s spot them and re-assign them
[56]:
#search for mis-assigned peaks in module #0
labels = []
errors = []
for lbl,sg in gonio0.single_geometries.items():
labels.append(lbl)
errors.append(sg.geometry_refinement.chi2())
s = numpy.argsort(errors)
for i in s[-10:]:
print(labels[i], errors[i])
data_02_0455 6.313036491714458e-07
data_02_0464 6.523609473021892e-07
data_02_0465 6.891634832505096e-07
data_02_0457 7.370411378714757e-07
data_02_0456 7.376222637955442e-07
data_02_0460 7.458553094683675e-07
data_02_0466 7.671412675214738e-07
data_02_0461 7.935692964121192e-07
data_02_0462 7.971540266865079e-07
data_02_0480 0.0011307661026103302
[57]:
#remove wrongly assigned peak for frame 480
print(gonio0.single_geometries.pop("data_02_0480").control_points)
gonio0.refine2()
gonio0 = complete_gonio(module_id=0)
gonio0.refine2()
ControlPoints instance containing 4 group of point:
LaB6 Calibrant with 109 reflections at wavelength 7.281587910025816e-11
Containing 4 groups of points:
#psg ring 52: 1 points
#psh ring 53: 1 points
#psi ring 54: 1 points
#psj ring 55: 1 points
Cost function before refinement: 8.041213618478122e-09
[ 7.21973752e-01 3.22003152e-02 3.94381146e-03 4.51420922e-05
-8.27999423e+01 9.99140787e-01 1.70270825e+01]
message: Optimization terminated successfully
success: True
status: 0
fun: 9.214244602861188e-10
x: [ 7.206e-01 3.228e-02 4.043e-03 -2.053e-05 -8.280e+01
9.990e-01 1.703e+01]
nit: 9
jac: [-3.087e-08 -3.829e-08 -1.829e-07 1.319e-07 -8.443e-10
-1.615e-08 nan]
nfev: 64
njev: 9
Cost function after refinement: 9.214244602861188e-10
GonioParam(dist=0.7205957894276002, poni1=0.032284408312060156, poni2=0.004042525656543217, rot1=-2.0533943479941534e-05, offset=-82.79994103817624, scale=0.9989751747980284, nrj=17.027082549190933)
maxdelta on: dist (0) 0.7219737518819529 --> 0.7205957894276002
Number of peaks previously found: 1246
Number of peaks found after re-scan: 1263
Cost function before refinement: 9.385075964190633e-10
[ 7.20595789e-01 3.22844083e-02 4.04252566e-03 -2.05339435e-05
-8.27999410e+01 9.98975175e-01 1.70270825e+01]
message: Optimization terminated successfully
success: True
status: 0
fun: 9.382098584456135e-10
x: [ 7.206e-01 3.228e-02 4.043e-03 -2.057e-05 -8.280e+01
9.990e-01 1.703e+01]
nit: 1
jac: [-2.666e-08 -1.466e-06 -1.817e-07 1.310e-07 -1.881e-08
-4.389e-08 nan]
nfev: 9
njev: 1
Cost function after refinement: 9.382098584456135e-10
GonioParam(dist=0.7205957964378075, poni1=0.03228479377833516, poni2=0.004042573433038651, rot1=-2.0568399467646526e-05, offset=-82.79994103322964, scale=0.9989751863383792, nrj=17.027082549190933)
maxdelta on: poni1 (1) 0.032284408312060156 --> 0.03228479377833516
[57]:
array([ 7.20595796e-01, 3.22847938e-02, 4.04257343e-03, -2.05683995e-05,
-8.27999410e+01, 9.98975186e-01, 1.70270825e+01])
[58]:
def search_outliers(module_id=None, name=None, threshold=1.2):
"Search for wrongly assigned peaks"
if name is None:
name = ds_names[module_id]
gonioref = goniometers[name]
labels = []
errors = []
for lbl,sg in gonioref.single_geometries.items():
labels.append(lbl)
errors.append(sg.geometry_refinement.chi2())
s = numpy.argsort(errors)
last = errors[s[-1]]
to_remove = []
for i in s[-1::-1]:
lbl = labels[i]
current = errors[i]
print(lbl , current, last, last/current)
if threshold*current<last:
break
last=current
to_remove.append(lbl)
return to_remove
for lbl in search_outliers(8):
gonio8.single_geometries.pop(lbl)
gonio8.refine2()
gonio8 = complete_gonio(module_id=8)
gonio8.refine2()
data_11_0495 1.4653264249059768e-06 1.4653264249059768e-06 1.0
data_11_0496 1.4360706723755973e-06 1.4653264249059768e-06 1.02037208411337
data_11_0499 1.4166274579074244e-06 1.4360706723755973e-06 1.01372500184127
data_11_0497 1.408429897528043e-06 1.4166274579074244e-06 1.0058203538520227
data_11_0498 1.3832745250176507e-06 1.408429897528043e-06 1.0181853797315261
data_11_0500 1.3708837484730059e-06 1.3832745250176507e-06 1.0090385319385737
data_11_0492 1.3295635096461316e-06 1.3708837484730059e-06 1.031078048191825
data_11_0489 1.3287444389906674e-06 1.3295635096461316e-06 1.000616424521849
data_11_0491 1.3215889751725488e-06 1.3287444389906674e-06 1.0054142883699408
data_11_0490 1.301797579301906e-06 1.3215889751725488e-06 1.0152031284934913
data_11_0494 1.2865330382410883e-06 1.301797579301906e-06 1.0118648651896938
data_11_0493 1.2861198600876661e-06 1.2865330382410883e-06 1.0003212594457518
data_11_0483 1.2244247451147827e-06 1.2861198600876661e-06 1.0503870206960737
data_11_0486 1.2073493928202727e-06 1.2244247451147827e-06 1.0141428424912058
data_11_0485 1.2017864447477076e-06 1.2073493928202727e-06 1.0046288990002155
data_11_0484 1.1994579208818936e-06 1.2017864447477076e-06 1.001941313509441
data_11_0487 1.1764421082529778e-06 1.1994579208818936e-06 1.0195639143375226
data_11_0477 1.1389376208111523e-06 1.1764421082529778e-06 1.032929360446549
data_11_0478 1.1156529806479392e-06 1.1389376208111523e-06 1.0208708626849992
data_11_0481 1.1104608438547017e-06 1.1156529806479392e-06 1.0046756594993609
data_11_0479 1.1057542147544931e-06 1.1104608438547017e-06 1.004256487596797
data_11_0480 1.100219756303158e-06 1.1057542147544931e-06 1.0050303209150975
data_11_0482 8.673122808931536e-07 1.100219756303158e-06 1.2685393491374957
Cost function before refinement: 1.0594738330129545e-09
[ 7.20813436e-01 3.20849187e-02 3.96153992e-03 2.77057943e-05
-3.71999988e+01 9.98991357e-01 1.70270825e+01]
message: Optimization terminated successfully
success: True
status: 0
fun: 1.058942401027041e-09
x: [ 7.208e-01 3.209e-02 3.962e-03 2.762e-05 -3.720e+01
9.990e-01 1.703e+01]
nit: 1
jac: [-8.451e-07 -1.253e-06 -2.518e-07 1.849e-07 -1.614e-08
9.174e-08 nan]
nfev: 9
njev: 1
Cost function after refinement: 1.058942401027041e-09
GonioParam(dist=0.7208138055232528, poni1=0.032085466901616906, poni2=0.003961650091808378, rot1=2.7624888069974965e-05, offset=-37.199998778669595, scale=0.9989913173312018, nrj=17.027082549190933)
maxdelta on: poni1 (1) 0.03208491868712114 --> 0.032085466901616906
Number of peaks previously found: 918
Number of peaks found after re-scan: 1006
Cost function before refinement: 9.804575919262705e-10
[ 7.20813806e-01 3.20854669e-02 3.96165009e-03 2.76248881e-05
-3.71999988e+01 9.98991317e-01 1.70270825e+01]
message: Optimization terminated successfully
success: True
status: 0
fun: 9.797990703945884e-10
x: [ 7.208e-01 3.209e-02 3.962e-03 2.759e-05 -3.720e+01
9.990e-01 1.703e+01]
nit: 1
jac: [-8.288e-07 2.044e-06 -2.226e-07 1.638e-07 2.536e-08
1.004e-06 nan]
nfev: 9
njev: 1
Cost function after refinement: 9.797990703945884e-10
GonioParam(dist=0.7208139925217619, poni1=0.03208500579368141, poni2=0.003961700325261782, rot1=2.7587922571998175e-05, offset=-37.19999878439213, scale=0.9989910907857577, nrj=17.027082549190933)
maxdelta on: poni1 (1) 0.032085466901616906 --> 0.03208500579368141
[58]:
array([ 7.20813993e-01, 3.20850058e-02, 3.96170033e-03, 2.75879226e-05,
-3.71999988e+01, 9.98991091e-01, 1.70270825e+01])
[59]:
print(gonio7.chi2())
for lbl in search_outliers(7):
gonio7.single_geometries.pop(lbl)
gonio7.refine2()
gonio7 = complete_gonio(module_id=7)
gonio7.refine2()
6.982166320635817e-10
data_10_0292 4.478313610295236e-06 4.478313610295236e-06 1.0
data_10_0291 4.441618075732054e-06 4.478313610295236e-06 1.008261749195339
data_10_0288 4.421114039991817e-06 4.441618075732054e-06 1.0046377531895274
data_10_0285 4.4151969079424084e-06 4.421114039991817e-06 1.0013401739883365
data_10_0290 4.4114083219467785e-06 4.4151969079424084e-06 1.0008588155344365
data_10_0289 4.40450577270408e-06 4.4114083219467785e-06 1.0015671563618955
data_10_0284 4.386350135873239e-06 4.40450577270408e-06 1.0041391216543243
data_10_0275 4.376873169865872e-06 4.386350135873239e-06 1.0021652366060354
data_10_0286 4.374944729160871e-06 4.376873169865872e-06 1.0004407920155303
data_10_0283 4.360029737297362e-06 4.374944729160871e-06 1.0034208463616476
data_10_0281 4.3581187741366675e-06 4.360029737297362e-06 1.0004384834970619
data_10_0282 4.3552714424913155e-06 4.3581187741366675e-06 1.0006537667474804
data_10_0278 4.352333646868408e-06 4.3552714424913155e-06 1.0006749932016406
data_10_0280 4.3515501506852325e-06 4.352333646868408e-06 1.0001800499031481
data_10_0277 4.349866613398178e-06 4.3515501506852325e-06 1.0003870319337769
data_10_0276 4.3396700589153925e-06 4.349866613398178e-06 1.0023496151422475
data_10_0279 4.338090818701843e-06 4.3396700589153925e-06 1.0003640403761813
data_10_0274 4.337324373540883e-06 4.338090818701843e-06 1.0001767092094
data_10_0287 4.319689618966426e-06 4.337324373540883e-06 1.004082412425427
data_10_0496 1.950808600710568e-06 4.319689618966426e-06 2.2143072454124972
Cost function before refinement: 6.590245000704119e-10
[ 7.20709214e-01 3.08662449e-02 3.96669077e-03 2.39914176e-05
-4.27999029e+01 9.99006688e-01 1.70270825e+01]
message: Optimization terminated successfully
success: True
status: 0
fun: 6.580239090129342e-10
x: [ 7.207e-01 3.087e-02 3.967e-03 2.397e-05 -4.280e+01
9.990e-01 1.703e+01]
nit: 2
jac: [-6.411e-07 8.001e-09 -1.445e-07 1.068e-07 -2.377e-10
-3.751e-07 nan]
nfev: 15
njev: 2
Cost function after refinement: 6.580239090129342e-10
GonioParam(dist=0.7207093528191252, poni1=0.030865644602940744, poni2=0.003966722983761047, rot1=2.3967642448708757e-05, offset=-42.7999029444283, scale=0.9990064423875449, nrj=17.027082549190933)
maxdelta on: poni1 (1) 0.03086624488803945 --> 0.030865644602940744
Number of peaks previously found: 985
Number of peaks found after re-scan: 1004
Cost function before refinement: 6.991408555023671e-10
[ 7.20709353e-01 3.08656446e-02 3.96672298e-03 2.39676424e-05
-4.27999029e+01 9.99006442e-01 1.70270825e+01]
message: Optimization terminated successfully
success: True
status: 0
fun: 6.980019785354917e-10
x: [ 7.207e-01 3.087e-02 3.967e-03 2.393e-05 -4.280e+01
9.990e-01 1.703e+01]
nit: 2
jac: [-6.609e-07 1.522e-07 -2.321e-07 1.700e-07 1.580e-09
9.613e-08 nan]
nfev: 15
njev: 2
Cost function after refinement: 6.980019785354917e-10
GonioParam(dist=0.7207094971168743, poni1=0.03086623823197484, poni2=0.003966772613855158, rot1=2.3931290270607465e-05, offset=-42.79990293688394, scale=0.9990067735018262, nrj=17.027082549190933)
maxdelta on: poni1 (1) 0.030865644602940744 --> 0.03086623823197484
[59]:
array([ 7.20709497e-01, 3.08662382e-02, 3.96677261e-03, 2.39312903e-05,
-4.27999029e+01, 9.99006774e-01, 1.70270825e+01])
[60]:
print(gonio0.chi2())
print(len(search_outliers(0)))
# for lbl in search_outliers(7):
# gonio7.single_geometries.pop(lbl)
# gonio7.refine2()
# gonio7 = complete_gonio(module_id=7)
# gonio7.refine2()
9.382098584456135e-10
data_02_0462 7.971540266865079e-07 7.971540266865079e-07 1.0
data_02_0461 7.935692964121192e-07 7.971540266865079e-07 1.0045172240037459
data_02_0466 7.671412675214738e-07 7.935692964121192e-07 1.0344500159351753
data_02_0460 7.458553094683675e-07 7.671412675214738e-07 1.0285389911191738
data_02_0456 7.376222637955442e-07 7.458553094683675e-07 1.011161601373661
data_02_0457 7.370411378714757e-07 7.376222637955442e-07 1.0007884579221
data_02_0465 6.891634832505096e-07 7.370411378714757e-07 1.069472129305439
data_02_0464 6.523609473021892e-07 6.891634832505096e-07 1.0564143762751521
data_02_0455 6.313036491714458e-07 6.523609473021892e-07 1.033355261225529
data_02_0463 6.240792201950713e-07 6.313036491714458e-07 1.0115761408849928
data_02_0459 6.163883776139301e-07 6.240792201950713e-07 1.0124772673536007
data_02_0448 6.082012730300175e-07 6.163883776139301e-07 1.013461176335796
data_02_0454 5.868915115543744e-07 6.082012730300175e-07 1.036309541126612
data_02_0439 5.868103847559679e-07 5.868915115543744e-07 1.0001382504476983
data_02_0435 5.859903705274693e-07 5.868103847559679e-07 1.0013993646819837
data_02_0426 5.755879595006237e-07 5.859903705274693e-07 1.0180726696157278
data_02_0458 5.724203268031596e-07 5.755879595006237e-07 1.0055337529943331
data_02_0453 5.590326059354276e-07 5.724203268031596e-07 1.0239480143476254
data_02_0434 5.570139568262492e-07 5.590326059354276e-07 1.0036240548094704
data_02_0444 5.52479378594903e-07 5.570139568262492e-07 1.0082076877563808
data_02_0430 5.489352109509736e-07 5.52479378594903e-07 1.0064564407114447
data_02_0443 5.459467109203509e-07 5.489352109509736e-07 1.0054739775345192
data_02_0447 5.424204366818411e-07 5.459467109203509e-07 1.0065009981188784
data_02_0468 5.360711310359359e-07 5.424204366818411e-07 1.0118441476854674
data_02_0425 5.340449210573293e-07 5.360711310359359e-07 1.0037940815439177
data_02_0467 5.066722866428126e-07 5.340449210573293e-07 1.0540243371033504
data_02_0438 5.014369370144399e-07 5.066722866428126e-07 1.0104406940173654
data_02_0429 4.99403819968963e-07 5.014369370144399e-07 1.0040710882940447
data_02_0442 4.988909715188969e-07 4.99403819968963e-07 1.0010279770117
data_02_0421 4.887204776036332e-07 4.988909715188969e-07 1.0208104517435677
data_02_0452 4.818394342566045e-07 4.887204776036332e-07 1.0142807808116514
data_02_0441 4.7080818883309074e-07 4.818394342566045e-07 1.0234304451051603
data_02_0433 4.6907497808393685e-07 4.7080818883309074e-07 1.0036949546024256
data_02_0437 4.674409673906393e-07 4.6907497808393685e-07 1.0034956514453985
data_02_0420 4.599762568493357e-07 4.674409673906393e-07 1.0162284692528132
data_02_0451 4.5329033193163294e-07 4.599762568493357e-07 1.0147497628930484
data_02_0446 4.4537883049631956e-07 4.5329033193163294e-07 1.0177635327357095
data_02_0428 4.42456525822236e-07 4.4537883049631956e-07 1.0066047272523622
data_02_0424 4.3749902020266474e-07 4.42456525822236e-07 1.0113314667933995
data_02_0432 4.3734551969408895e-07 4.3749902020266474e-07 1.0003509822363863
data_02_0436 4.331866832386705e-07 4.3734551969408895e-07 1.0096005639516095
data_02_0450 4.262100092982173e-07 4.331866832386705e-07 1.0163690992427437
data_02_0445 4.1944397535287247e-07 4.262100092982173e-07 1.0161309598967363
data_02_0427 4.1840555392472044e-07 4.1944397535287247e-07 1.0024818538339453
data_02_0423 4.1311968681592694e-07 4.1840555392472044e-07 1.0127950017331144
data_02_0419 3.8768788546419296e-07 4.1311968681592694e-07 1.0655986485656717
data_02_0408 3.5423439589395346e-07 3.8768788546419296e-07 1.0944388516699954
data_02_0418 3.436567691349336e-07 3.5423439589395346e-07 1.0307796258041018
data_02_0412 3.4365078751307176e-07 3.436567691349336e-07 1.0000174061054978
data_02_0398 3.357911671477211e-07 3.4365078751307176e-07 1.0234062748943396
data_02_0389 3.2715497286197265e-07 3.357911671477211e-07 1.0263978695179181
data_02_0394 3.213836275958599e-07 3.2715497286197265e-07 1.017957807338494
data_02_0416 3.19468056079038e-07 3.213836275958599e-07 1.005996128502901
data_02_0403 3.0713355118444586e-07 3.19468056079038e-07 1.0401600699338276
data_02_0411 3.0688035367483995e-07 3.0713355118444586e-07 1.0008250691403797
data_02_0407 3.0628805841467744e-07 3.0688035367483995e-07 1.0019337850232497
data_02_0402 3.049021454711834e-07 3.0628805841467744e-07 1.0045454351964376
data_02_0393 2.980908450430102e-07 3.049021454711834e-07 1.0228497471205142
data_02_0388 2.945097819229645e-07 2.980908450430102e-07 1.012159402980314
data_02_0397 2.9208255748953456e-07 2.945097819229645e-07 1.0083100629297828
data_02_0384 2.8246444537231956e-07 2.9208255748953456e-07 1.0340507000962094
data_02_0406 2.817235681006301e-07 2.8246444537231956e-07 1.0026298022443931
data_02_0401 2.815310734578888e-07 2.817235681006301e-07 1.0006837420835186
data_02_0417 2.810858349891032e-07 2.815310734578888e-07 1.001583994685477
data_02_0392 2.739812164821265e-07 2.810858349891032e-07 1.025931042274353
data_02_0410 2.7025873203608476e-07 2.739812164821265e-07 1.0137737804732418
data_02_0415 2.6501792601213064e-07 2.7025873203608476e-07 1.0197752887995744
data_02_0405 2.6433960353472077e-07 2.6501792601213064e-07 1.0025661023484163
data_02_0414 2.5775846420670583e-07 2.6433960353472077e-07 1.0255321948331337
data_02_0396 2.570083223372203e-07 2.5775846420670583e-07 1.002918745442419
data_02_0391 2.485179006235142e-07 2.570083223372203e-07 1.0341642259668387
data_02_0387 2.4757387983640684e-07 2.485179006235142e-07 1.0038130871791933
data_02_0383 2.436324190464806e-07 2.4757387983640684e-07 1.0161778994985649
data_02_0400 2.4112108284998156e-07 2.436324190464806e-07 1.0104152493295724
data_02_0395 2.386285458278207e-07 2.4112108284998156e-07 1.0104452592354953
data_02_0399 2.3072425986983e-07 2.386285458278207e-07 1.0342585819213381
data_02_0386 2.2832961753069427e-07 2.3072425986983e-07 1.0104876553687294
data_02_0409 2.2099254926714062e-07 2.2832961753069427e-07 1.0332005232207373
data_02_0404 2.200632149826795e-07 2.2099254926714062e-07 1.0042230332976563
data_02_0390 2.1855316188101852e-07 2.200632149826795e-07 1.0069093171138062
data_02_0382 2.1738312055544068e-07 2.1855316188101852e-07 1.005382392720227
data_02_0381 2.0686219013436962e-07 2.1738312055544068e-07 1.0508596105176933
data_02_0413 2.0388152591107816e-07 2.0686219013436962e-07 1.0146195895384433
data_02_0385 2.0140303101946426e-07 2.0388152591107816e-07 1.0123061449426467
data_02_0360 1.9864896885838632e-07 2.0140303101946426e-07 1.0138639640412193
data_02_0375 1.9263546030346346e-07 1.9864896885838632e-07 1.0312170383658836
data_02_0370 1.920301959625982e-07 1.9263546030346346e-07 1.003151922737105
data_02_0365 1.911260411714131e-07 1.920301959625982e-07 1.0047306729404508
data_02_0380 1.896072216244721e-07 1.911260411714131e-07 1.0080103465149082
data_02_0369 1.7565559633410337e-07 1.896072216244721e-07 1.0794260221794028
data_02_0355 1.710407884427107e-07 1.7565559633410337e-07 1.026980744963874
data_02_0374 1.6999503262094926e-07 1.710407884427107e-07 1.0061516845853562
data_02_0364 1.694072168719141e-07 1.6999503262094926e-07 1.0034698388881484
data_02_0350 1.6598943575407027e-07 1.694072168719141e-07 1.0205903532493936
data_02_0363 1.574813568972464e-07 1.6598943575407027e-07 1.0540259432891173
data_02_0373 1.5391536774940503e-07 1.574813568972464e-07 1.0231685061731282
data_02_0354 1.5253343428684397e-07 1.5391536774940503e-07 1.009059872473351
data_02_0358 1.5111664301393935e-07 1.5253343428684397e-07 1.0093754813807896
data_02_0349 1.4524820316105622e-07 1.5111664301393935e-07 1.040402839588838
data_02_0368 1.4209150109826283e-07 1.4524820316105622e-07 1.0222159808179547
data_02_0359 1.3720532981184415e-07 1.4209150109826283e-07 1.0356121099167162
data_02_0379 1.370664499810907e-07 1.3720532981184415e-07 1.001013229939001
data_02_0367 1.3261331246263957e-07 1.370664499810907e-07 1.0335798679314772
data_02_0378 1.3251851947293534e-07 1.3261331246263957e-07 1.0007153188103914
data_02_0362 1.2827293192504197e-07 1.3251851947293534e-07 1.033098078325475
data_02_0372 1.274859702116593e-07 1.2827293192504197e-07 1.0061729279863196
data_02_0344 1.2738008290496092e-07 1.274859702116593e-07 1.0008312705117124
data_02_0353 1.270493714215481e-07 1.2738008290496092e-07 1.0026030155026546
data_02_0345 1.2601084004776139e-07 1.270493714215481e-07 1.0082416034477122
data_02_0343 1.216743457485912e-07 1.2601084004776139e-07 1.0356401694415556
data_02_0357 1.1836469442237941e-07 1.216743457485912e-07 1.02796147400509
data_02_0348 1.1627475678612285e-07 1.1836469442237941e-07 1.0179741303617673
data_02_0371 1.1505415954033668e-07 1.1627475678612285e-07 1.0106088928089405
data_02_0366 1.144487086545646e-07 1.1505415954033668e-07 1.0052901504341083
data_02_0352 1.1166503411858944e-07 1.144487086545646e-07 1.0249287931351803
data_02_0356 1.1066798028785224e-07 1.1166503411858944e-07 1.0090094156244998
data_02_0377 1.0535396343349566e-07 1.1066798028785224e-07 1.0504396482217875
data_02_0351 1.024389106065953e-07 1.0535396343349566e-07 1.0284564996800414
data_02_0361 1.015376647151082e-07 1.024389106065953e-07 1.0088759761613169
data_02_0347 1.013401128814537e-07 1.015376647151082e-07 1.0019493942530497
data_02_0376 9.83230223927681e-08 1.013401128814537e-07 1.030685493745639
data_02_0342 9.289928398112562e-08 9.83230223927681e-08 1.0583829947789956
data_02_0329 9.16005199927433e-08 9.289928398112562e-08 1.0141785656728282
data_02_0346 9.116941174584917e-08 9.16005199927433e-08 1.0047286500882109
data_02_0111 9.09158982411786e-08 9.116941174584917e-08 1.002788439751187
data_02_0074 9.069441044346989e-08 9.09158982411786e-08 1.0024421328351514
data_02_0137 9.032976894843263e-08 9.069441044346989e-08 1.004036781000131
data_02_0095 8.745284939511447e-08 9.032976894843263e-08 1.0328968075164728
data_02_0148 8.648921735282278e-08 8.745284939511447e-08 1.0111416436844451
data_02_0125 8.424420227332979e-08 8.648921735282278e-08 1.0266488971218346
data_02_0334 8.326862448084429e-08 8.424420227332979e-08 1.0117160310809497
data_02_0112 8.320697701582237e-08 8.326862448084429e-08 1.0007408929783639
data_02_0075 8.138269794869593e-08 8.320697701582237e-08 1.02241605541606
data_02_0126 8.103535619957762e-08 8.138269794869593e-08 1.0042862987886776
data_02_0096 8.045292747184154e-08 8.103535619957762e-08 1.007239372711949
data_02_0076 8.031608553391842e-08 8.045292747184154e-08 1.0017037924223202
data_02_0341 7.826189678569166e-08 8.031608553391842e-08 1.0262476228227875
data_02_0138 7.734409220420543e-08 7.826189678569166e-08 1.0118665117829948
data_02_0313 7.682169383541839e-08 7.734409220420543e-08 1.0068001412453391
data_02_0097 7.680679419341013e-08 7.682169383541839e-08 1.0001939885939093
data_02_0176 7.667729640743856e-08 7.680679419341013e-08 1.0016888673967252
data_02_0328 7.592389914455753e-08 7.667729640743856e-08 1.0099230581064675
data_02_0113 7.555667819876745e-08 7.592389914455753e-08 1.0048602050082724
data_02_0327 7.544624001244896e-08 7.555667819876745e-08 1.001463799737406
data_02_0127 7.131653040419096e-08 7.544624001244896e-08 1.0579067655822936
data_02_0312 6.911490652182211e-08 7.131653040419096e-08 1.0318545447453324
data_02_0139 6.90931164939152e-08 6.911490652182211e-08 1.000315371906966
data_02_0340 6.902050869991086e-08 6.90931164939152e-08 1.0010519741939317
data_02_0333 6.774036313340146e-08 6.902050869991086e-08 1.018897825569497
data_02_0307 6.766457491542204e-08 6.774036313340146e-08 1.0011200575496728
data_02_0185 6.763925664301622e-08 6.766457491542204e-08 1.0003743132858398
data_02_0150 6.745630599854259e-08 6.763925664301622e-08 1.0027121355337423
data_02_0177 6.735831856953238e-08 6.745630599854259e-08 1.0014547190471963
data_02_0193 6.662205552089285e-08 6.735831856953238e-08 1.0110513409243076
data_02_0208 6.626147902975876e-08 6.662205552089285e-08 1.0054417211389464
data_02_0098 6.59226867430583e-08 6.626147902975876e-08 1.0051392366336789
data_02_0302 6.582977316743616e-08 6.59226867430583e-08 1.0014114217800176
data_02_0140 6.576202833197386e-08 6.582977316743616e-08 1.001030151246557
data_02_0077 6.529938573091631e-08 6.576202833197386e-08 1.0070849456833177
data_02_0201 6.303184379764337e-08 6.529938573091631e-08 1.0359745455099272
data_02_0114 6.245919214643206e-08 6.303184379764337e-08 1.009168412711275
data_02_0318 6.239184702937052e-08 6.245919214643206e-08 1.0010793897002255
data_02_0178 6.168572229146186e-08 6.239184702937052e-08 1.0114471341451146
data_02_0326 6.156213199765569e-08 6.168572229146186e-08 1.0020075700726363
data_02_0215 6.154481021597962e-08 6.156213199765569e-08 1.0002814499161712
data_02_0311 6.138471473893103e-08 6.154481021597962e-08 1.0026080674599447
data_02_0099 6.073035821178917e-08 6.138471473893103e-08 1.0107747845790713
data_02_0301 6.069712736926435e-08 6.073035821178917e-08 1.0005474862479513
data_02_0186 6.06185298751725e-08 6.069712736926435e-08 1.001296591887888
data_02_0078 6.055512834877297e-08 6.06185298751725e-08 1.001047005070064
data_02_0079 5.949127153350898e-08 6.055512834877297e-08 1.0178825697928604
data_02_0306 5.912441694744221e-08 5.949127153350898e-08 1.006204789916032
data_02_0332 5.727315593013976e-08 5.912441694744221e-08 1.0323233631399773
data_02_0141 5.719417876988802e-08 5.727315593013976e-08 1.0013808601146192
data_02_0115 5.7162648432152425e-08 5.719417876988802e-08 1.0005515898685664
data_02_0128 5.695548290502778e-08 5.7162648432152425e-08 1.003637323687872
data_02_0168 5.679705522484517e-08 5.695548290502778e-08 1.0027893643350951
data_02_0100 5.659624831555914e-08 5.679705522484517e-08 1.0035480604326705
data_02_0216 5.525232626983928e-08 5.659624831555914e-08 1.0243233567968968
data_02_0217 5.4764481465418027e-08 5.525232626983928e-08 1.0089080511924378
data_02_0278 5.440683377108302e-08 5.4764481465418027e-08 1.0065735803674922
data_02_0194 5.33628932458377e-08 5.440683377108302e-08 1.0195630420643795
data_02_0169 5.3331628241844825e-08 5.33628932458377e-08 1.0005862375671544
data_02_0325 5.3061665141943205e-08 5.3331628241844825e-08 1.0050877238620284
data_02_0284 5.276552648610089e-08 5.3061665141943205e-08 1.0056123510095236
data_02_0151 5.2367054005389306e-08 5.276552648610089e-08 1.0076092208790393
data_02_0116 5.235341210012136e-08 5.2367054005389306e-08 1.0002605733746992
data_02_0129 5.1837395523233295e-08 5.235341210012136e-08 1.0099545235959393
data_02_0209 5.18370655523612e-08 5.1837395523233295e-08 1.0000063655391866
data_02_0101 5.166973621609745e-08 5.18370655523612e-08 1.0032384399170131
data_02_0331 5.107872558725756e-08 5.166973621609745e-08 1.011570582900121
data_02_0117 5.101371818979342e-08 5.107872558725756e-08 1.001274312082532
data_02_0170 4.9929646401594325e-08 5.101371818979342e-08 1.0217119860909827
data_02_0202 4.979995439523293e-08 4.9929646401594325e-08 1.0026042595407236
data_02_0187 4.912204765516747e-08 4.979995439523293e-08 1.0138004576849953
data_02_0195 4.909544260249187e-08 4.912204765516747e-08 1.000541904732197
data_02_0179 4.884857389359304e-08 4.909544260249187e-08 1.0050537546794422
data_02_0152 4.8736577849243335e-08 4.884857389359304e-08 1.0022979874519737
data_02_0338 4.863240901971703e-08 4.8736577849243335e-08 1.0021419631810562
data_02_0080 4.7763667151372616e-08 4.863240901971703e-08 1.0181883410583028
data_02_0300 4.7307711300649533e-08 4.7763667151372616e-08 1.0096380872840243
data_02_0289 4.716164970271535e-08 4.7307711300649533e-08 1.0030970417458864
data_02_0305 4.694853706025366e-08 4.716164970271535e-08 1.0045392818563905
data_02_0130 4.6783797253514985e-08 4.694853706025366e-08 1.003521300458917
data_02_0317 4.67657228043495e-08 4.6783797253514985e-08 1.0003864892507082
data_02_0142 4.632766607135677e-08 4.67657228043495e-08 1.0094556184271837
data_02_0203 4.572492026730186e-08 4.632766607135677e-08 1.013181997924356
data_02_0180 4.5156858808528775e-08 4.572492026730186e-08 1.0125797381341723
data_02_0236 4.490529842713039e-08 4.5156858808528775e-08 1.0056020200334845
data_02_0210 4.400391313944352e-08 4.490529842713039e-08 1.0204842075028755
data_02_0081 4.364523998775825e-08 4.400391313944352e-08 1.0082179213995814
data_02_0131 4.354491436440689e-08 4.364523998775825e-08 1.0023039573005421
data_02_0310 4.337830735352795e-08 4.354491436440689e-08 1.0038407909631215
data_02_0153 4.31781464846463e-08 4.337830735352795e-08 1.0046356984997684
data_02_0339 4.314212949863592e-08 4.31781464846463e-08 1.0008348448819966
data_02_0196 4.23775505358902e-08 4.314212949863592e-08 1.0180420754167514
data_02_0188 4.2228755701222894e-08 4.23775505358902e-08 1.0035235429554226
data_02_0229 4.2089051413528255e-08 4.2228755701222894e-08 1.0033192548418834
data_02_0290 4.153886120248492e-08 4.2089051413528255e-08 1.0132451924563215
data_02_0172 4.115914233205105e-08 4.153886120248492e-08 1.0092256264081134
data_02_0102 4.110162871665345e-08 4.115914233205105e-08 1.0013993025871089
data_02_0330 4.090697306450536e-08 4.110162871665345e-08 1.0047584956198332
data_02_0337 4.052173813148013e-08 4.090697306450536e-08 1.0095068708991521
data_02_0309 3.9744054468036604e-08 4.052173813148013e-08 1.0195672956333373
data_02_0232 3.958823021675607e-08 3.9744054468036604e-08 1.003936125722907
data_02_0171 3.9523838882891047e-08 3.958823021675607e-08 1.00162917711652
data_02_0230 3.9452295301997494e-08 3.9523838882891047e-08 1.0018134199885178
data_02_0242 3.9216491298397226e-08 3.9452295301997494e-08 1.0060128786587774
data_02_0316 3.909765321726841e-08 3.9216491298397226e-08 1.003039519545289
data_02_0239 3.897254103689109e-08 3.909765321726841e-08 1.0032102648954526
data_02_0237 3.875842749117757e-08 3.897254103689109e-08 1.005524309410186
data_02_0299 3.859061375036245e-08 3.875842749117757e-08 1.0043485636663019
data_02_0324 3.826965217976124e-08 3.859061375036245e-08 1.0083868431595244
data_02_0249 3.810910320273194e-08 3.826965217976124e-08 1.0042128773320962
data_02_0143 3.8107526237647436e-08 3.810910320273194e-08 1.0000413819851404
data_02_0118 3.810108545745867e-08 3.8107526237647436e-08 1.0001690445327591
data_02_0189 3.8002440706154374e-08 3.810108545745867e-08 1.0025957477854395
data_02_0082 3.774230173608561e-08 3.8002440706154374e-08 1.0068925041161452
data_02_0238 3.7560085646901294e-08 3.774230173608561e-08 1.004851322515537
data_02_0323 3.7515177979767095e-08 3.7560085646901294e-08 1.0011970532875631
data_02_0181 3.70626977416921e-08 3.7515177979767095e-08 1.0122085078973082
data_02_0231 3.682097870952214e-08 3.70626977416921e-08 1.0065647095933234
data_02_0103 3.677844957399585e-08 3.682097870952214e-08 1.0011563602060147
data_02_0255 3.628478587594827e-08 3.677844957399585e-08 1.013605253169616
data_02_0204 3.616482722772049e-08 3.628478587594827e-08 1.003316997685968
data_02_0272 3.599235964365634e-08 3.616482722772049e-08 1.0047917831943132
data_02_0154 3.593898072303098e-08 3.599235964365634e-08 1.001485265289985
data_02_0083 3.5895020334709865e-08 3.593898072303098e-08 1.0012246932279518
data_02_0315 3.5408373834389536e-08 3.5895020334709865e-08 1.0137438251922115
data_02_0271 3.540525678042462e-08 3.5408373834389536e-08 1.0000880392983518
data_02_0132 3.539145384780218e-08 3.540525678042462e-08 1.0003900075052525
data_02_0211 3.5318224781573855e-08 3.539145384780218e-08 1.0020734073323676
data_02_0283 3.508224638393394e-08 3.5318224781573855e-08 1.0067264335087729
data_02_0304 3.46939405835159e-08 3.508224638393394e-08 1.0111923233246825
data_02_0266 3.438015300024862e-08 3.46939405835159e-08 1.009126997871854
data_02_0282 3.4240456183147185e-08 3.438015300024862e-08 1.004079876049379
data_02_0308 3.402620683267746e-08 3.4240456183147185e-08 1.0062965981345875
data_02_0259 3.3943817851300015e-08 3.402620683267746e-08 1.0024272161056949
data_02_0119 3.3927967732563694e-08 3.3943817851300015e-08 1.0004671697067522
data_02_0253 3.3906643227995556e-08 3.3927967732563694e-08 1.0006289181864672
data_02_0197 3.380954203638034e-08 3.3906643227995556e-08 1.0028720055276328
data_02_0251 3.359311746412807e-08 3.380954203638034e-08 1.0064425271778772
data_02_0144 3.324769307344446e-08 3.359311746412807e-08 1.0103894243104496
data_02_0182 3.304671658618233e-08 3.324769307344446e-08 1.006081587159741
data_02_0336 3.2916902236036773e-08 3.304671658618233e-08 1.0039436988697994
data_02_0264 3.273171534614387e-08 3.2916902236036773e-08 1.0056577202854944
data_02_0104 3.252847857592453e-08 3.273171534614387e-08 1.0062479642183375
data_02_0298 3.2495936136271714e-08 3.252847857592453e-08 1.0010014310563744
data_02_0250 3.2424764651418045e-08 3.2495936136271714e-08 1.0021949730589812
data_02_0256 3.2363282384610147e-08 3.2424764651418045e-08 1.0018997537418248
data_02_0173 3.233329242773447e-08 3.2363282384610147e-08 1.0009275256128867
data_02_0258 3.226936799352002e-08 3.233329242773447e-08 1.0019809633156522
data_02_0243 3.217054250479955e-08 3.226936799352002e-08 1.0030719248426017
data_02_0190 3.214097411475764e-08 3.217054250479955e-08 1.0009199593620386
data_02_0262 3.1932167695326754e-08 3.214097411475764e-08 1.0065390618458214
data_02_0269 3.1518173981986e-08 3.1932167695326754e-08 1.0131350792586324
data_02_0120 3.1505053151953135e-08 3.1518173981986e-08 1.0004164674780767
data_02_0191 3.141979540670374e-08 3.1505053151953135e-08 1.0027135041506732
data_02_0261 3.124495944635774e-08 3.141979540670374e-08 1.0055956532971715
data_02_0218 3.055803606392995e-08 3.124495944635774e-08 1.022479304003395
data_02_0252 3.018652396532365e-08 3.055803606392995e-08 1.0123072169234548
data_02_0322 3.011743875604037e-08 3.018652396532365e-08 1.0022938607045202
data_02_0314 3.0097930406807425e-08 3.011743875604037e-08 1.0006481624805847
data_02_0265 3.00515531663903e-08 3.0097930406807425e-08 1.0015432560227533
data_02_0268 2.9905630412435414e-08 3.00515531663903e-08 1.004879440825772
data_02_0155 2.979168606021535e-08 2.9905630412435414e-08 1.0038247030392895
data_02_0267 2.959674115223327e-08 2.979168606021535e-08 1.0065867017919088
data_02_0198 2.8804746879771473e-08 2.959674115223327e-08 1.027495269295978
data_02_0084 2.8541798370207324e-08 2.8804746879771473e-08 1.0092127519840735
data_02_0303 2.8462045177166852e-08 2.8541798370207324e-08 1.0028020893278762
data_02_0257 2.84619849607659e-08 2.8462045177166852e-08 1.0000021156781944
data_02_0281 2.844564031443896e-08 2.84619849607659e-08 1.0005745923152465
data_02_0219 2.8276171686765055e-08 2.844564031443896e-08 1.0059933370596001
data_02_0174 2.7830204276391705e-08 2.8276171686765055e-08 1.0160245827139567
data_02_0212 2.7693017298617995e-08 2.7830204276391705e-08 1.0049538472566713
data_02_0133 2.7647612743784636e-08 2.7693017298617995e-08 1.0016422595055179
data_02_0297 2.742399964524251e-08 2.7647612743784636e-08 1.0081539199764729
data_02_0205 2.7192009285789882e-08 2.742399964524251e-08 1.0085315637036747
data_02_0321 2.6960862044686667e-08 2.7192009285789882e-08 1.0085734365881958
data_02_0277 2.6917629218358815e-08 2.6960862044686667e-08 1.001606115678953
data_02_0105 2.6824132024842366e-08 2.6917629218358815e-08 1.0034855626802708
data_02_0199 2.6596840541936688e-08 2.6824132024842366e-08 1.0085458076325755
data_02_0145 2.6322012612096534e-08 2.6596840541936688e-08 1.010440992255807
data_02_0134 2.588661423462738e-08 2.6322012612096534e-08 1.0168194408709788
data_02_0244 2.5860850926336772e-08 2.588661423462738e-08 1.0009962281737748
data_02_0288 2.5814316096620205e-08 2.5860850926336772e-08 1.001802675288487
data_02_0280 2.5567500765371216e-08 2.5814316096620205e-08 1.0096534789815388
data_02_0200 2.5161849095525086e-08 2.5567500765371216e-08 1.0161216955203134
data_02_0286 2.5066600585479665e-08 2.5161849095525086e-08 1.003799817598745
data_02_0085 2.5060021490244493e-08 2.5066600585479665e-08 1.0002625335033226
data_02_0270 2.5014775517562304e-08 2.5060021490244493e-08 1.0018087698868383
data_02_0263 2.4817548038766007e-08 2.5014775517562304e-08 1.0079470976942693
data_02_0156 2.4613448459163313e-08 2.4817548038766007e-08 1.0082921976553314
data_02_0276 2.4560452898896405e-08 2.4613448459163313e-08 1.0021577598949443
data_02_0285 2.4538549254818378e-08 2.4560452898896405e-08 1.0008926218029668
data_02_0121 2.4058596989283354e-08 2.4538549254818378e-08 1.0199493040158916
data_02_0296 2.405839871997145e-08 2.4058596989283354e-08 1.0000082411682594
data_02_0207 2.3903476052081983e-08 2.405839871997145e-08 1.0064811773631548
data_02_0449 2.3732450458975782e-08 2.3903476052081983e-08 1.0072064026174556
data_02_0275 2.3517628219451086e-08 2.3732450458975782e-08 1.0091345197534427
data_02_0183 2.3500585579617803e-08 2.3517628219451086e-08 1.000725200645556
data_02_0206 2.3061826926576378e-08 2.3500585579617803e-08 1.0190253206928632
data_02_0220 2.2994985104397943e-08 2.3061826926576378e-08 1.0029067999772547
data_02_0146 2.2740994949298897e-08 2.2994985104397943e-08 1.0111688233371194
data_02_0221 2.2573021854433983e-08 2.2740994949298897e-08 1.0074413207034538
data_02_0295 2.2222325010870083e-08 2.2573021854433983e-08 1.0157812849642132
data_02_0106 2.2203302797213507e-08 2.2222325010870083e-08 1.0008567290114587
data_02_0287 2.1985349022305534e-08 2.2203302797213507e-08 1.0099135917599873
data_02_0335 2.1740527315368754e-08 2.1985349022305534e-08 1.0112610749217528
data_02_0157 2.1600870527428213e-08 2.1740527315368754e-08 1.0064653314672298
data_02_0086 2.1281183987317782e-08 2.1600870527428213e-08 1.0150220279238666
data_02_0135 2.060532963668915e-08 2.1281183987317782e-08 1.032799977605077
data_02_0245 2.021471536951278e-08 2.060532963668915e-08 1.0193232632780713
data_02_0147 2.0122437868152768e-08 2.021471536951278e-08 1.0045858012813675
data_02_0122 2.0049348713409756e-08 2.0122437868152768e-08 1.0036454627922216
data_02_0107 1.9387318513901423e-08 2.0049348713409756e-08 1.0341475897780104
data_02_0184 1.932982128871685e-08 1.9387318513901423e-08 1.0029745347525865
data_02_0233 1.9242217938137572e-08 1.932982128871685e-08 1.004552663880064
data_02_0175 1.9131995590831726e-08 1.9242217938137572e-08 1.0057611526608685
data_02_0192 1.906093179977536e-08 1.9131995590831726e-08 1.0037282432885681
data_02_0214 1.866853198836985e-08 1.906093179977536e-08 1.0210193180508231
data_02_0246 1.8085096524630115e-08 1.866853198836985e-08 1.0322605667570064
data_02_0224 1.7865147451066153e-08 1.8085096524630115e-08 1.0123116293423504
data_02_0123 1.778411411472574e-08 1.7865147451066153e-08 1.0045565011457789
data_02_0234 1.7743073771607667e-08 1.778411411472574e-08 1.0023130345759903
data_02_0087 1.768951320824764e-08 1.7743073771607667e-08 1.0030278144304758
data_02_0136 1.6856225078377287e-08 1.768951320824764e-08 1.0494350381533095
data_02_0222 1.685223922581369e-08 1.6856225078377287e-08 1.0002365176823202
data_02_0223 1.6841136609881915e-08 1.685223922581369e-08 1.000659255737244
data_02_0108 1.6692846185776305e-08 1.6841136609881915e-08 1.0088834715455515
data_02_0124 1.649784658805764e-08 1.6692846185776305e-08 1.0118197000243547
data_02_0274 1.6468218420670362e-08 1.649784658805764e-08 1.0017991118790415
data_02_0158 1.609224391228375e-08 1.6468218420670362e-08 1.0233637092773382
data_02_0240 1.5068601573472125e-08 1.609224391228375e-08 1.0679321391451295
data_02_0320 1.5036954071778313e-08 1.5068601573472125e-08 1.0021046484243248
data_02_0247 1.4173929697596535e-08 1.5036954071778313e-08 1.0608881511757549
data_02_0248 1.4169017637897149e-08 1.4173929697596535e-08 1.0003466760946256
data_02_0088 1.387531962674457e-08 1.4169017637897149e-08 1.0211669366222367
data_02_0235 1.3468344564201617e-08 1.387531962674457e-08 1.0302171555385269
data_02_0160 1.3120041044574954e-08 1.3468344564201617e-08 1.0265474413108397
data_02_0161 1.2298607229417375e-08 1.3120041044574954e-08 1.0667907999527597
data_02_0260 1.2167259676309402e-08 1.2298607229417375e-08 1.0107951631346963
data_02_0159 1.1999983455730615e-08 1.2167259676309402e-08 1.0139397042667508
data_02_0294 1.1975930661632139e-08 1.1999983455730615e-08 1.0020084279692378
data_02_0273 1.1970561201325617e-08 1.1975930661632139e-08 1.000448555436643
data_02_0241 1.1800054102163205e-08 1.1970561201325617e-08 1.0144496879155118
data_02_0109 1.1756306999668193e-08 1.1800054102163205e-08 1.0037211602671015
data_02_0254 1.1681362011672839e-08 1.1756306999668193e-08 1.0064157747975333
data_02_0089 1.0944841611492818e-08 1.1681362011672839e-08 1.0672938381681671
data_02_0319 1.0710357720931692e-08 1.0944841611492818e-08 1.0218931894406165
data_02_0291 9.6476348944768e-09 1.0710357720931692e-08 1.1101537151932743
data_02_0110 9.297536383721325e-09 9.6476348944768e-09 1.0376549761470628
data_02_0090 8.946140193618794e-09 9.297536383721325e-09 1.0392790837721477
data_02_0440 8.921394731124998e-09 8.946140193618794e-09 1.0027737212890564
data_02_0292 8.845594599634719e-09 8.921394731124998e-09 1.0085692522573224
data_02_0293 8.013187887764542e-09 8.845594599634719e-09 1.1038795949289035
data_02_0091 5.400193227259109e-09 8.013187887764542e-09 1.4838705858367347
376
Overlay of the differents results
We are getting to an end. Here are the first actually integrated data
[61]:
fig, ax = plt.subplots()
summed, counted, radial = None, None, None
for i in range(9):
name = ds_names[i]
ds = data[name]
gonioref = goniometers[name]
mg = gonioref.get_mg(position)
mg.radial_range = (0, 95)
images = [i.reshape(-1, 1) for i in ds]
res_mg = mg.integrate1d(images, 50000)
results[name] = res_mg
if summed is None:
summed = res_mg.sum
counted = res_mg.count
else:
summed += res_mg.sum
counted += res_mg.count
radial = res_mg.radial
jupyter.plot1d(res_mg, label="%i %s"%(i, name), calibrant=LaB6, ax=ax )
ax.plot(radial, summed/counted, label="Merged")
ax.legend()
fig.show()
/tmp/ipykernel_367778/3999147500.py:22: RuntimeWarning: invalid value encountered in divide
ax.plot(radial, summed/counted, label="Merged")
/tmp/ipykernel_367778/3999147500.py:24: UserWarning: Matplotlib is currently using module://matplotlib_inline.backend_inline, which is a non-GUI backend, so cannot show the figure.
fig.show()
Multi-Gonio fit
Can we fit everything togeather ? Just assume energy and scale parameter of the goniometer are the same for all modules and fit everything.
[62]:
from scipy.optimize import minimize
class MultiGoniometer:
def __init__(self, list_of_goniometers,
param_name_split,
param_name_common):
self.nb_gonio = len(list_of_goniometers)
self.goniometers = list_of_goniometers
self.names_split = param_name_split
self.names_common = param_name_common
self.param = None
def init_param(self):
param = []
for gonio in self.goniometers:
param += list(gonio.param[:len(self.names_split)])
param += list(gonio.param[len(self.names_split):])
self.param = numpy.array(param)
def residu2(self, param):
"Actually performs the calulation of the average of the error squared"
sumsquare = 0.0
npt = 0
for idx, gonio in enumerate(self.goniometers):
gonio_param = numpy.concatenate((param[len(self.names_split)*idx:len(self.names_split)*(1+idx)],
param[len(self.names_split)*len(self.goniometers):]))
sumsquare += gonio.residu2(gonio_param)
return sumsquare
def chi2(self, param=None):
"""Calculate the average of the square of the error for a given parameter set
"""
if param is not None:
return self.residu2(param)
else:
if self.param is None:
self.init_param()
return self.residu2(self.param)
def refine2(self, method="slsqp", **options):
"""Geometry refinement tool
See https://docs.scipy.org/doc/scipy-0.18.1/reference/generated/scipy.optimize.minimize.html
:param method: name of the minimizer
:param options: options for the minimizer
"""
if method.lower() in ["simplex", "nelder-mead"]:
method = "Nelder-Mead"
former_error = self.chi2()
print("Cost function before refinement: %s" % former_error)
param = numpy.asarray(self.param, dtype=numpy.float64)
print(param)
res = minimize(self.residu2, param, method=method,
tol=1e-12,
options=options)
print(res)
newparam = res.x
new_error = res.fun
print("Cost function after refinement: %s" % new_error)
if new_error < former_error:
self.param = newparam
return self.param
def integrate(self, list_of_dataset, npt=50000, radial_range=(0,100)):
summed = None
counted = None
param = self.param
for idx, ds in enumerate(list_of_dataset):
gonio = self.goniometers[idx]
gonio_param = numpy.concatenate((param[len(self.names_split)*idx:len(self.names_split)*(1+idx)],
param[len(self.names_split)*len(self.goniometers):]))
print(gonio_param)
gonio.param = gonio_param
mg = gonio.get_mg(position)
mg.radial_range = radial_range
images = [i.reshape(-1, 1) for i in ds]
res_mg = mg.integrate1d(images, 50000)
if summed is None:
summed = res_mg.sum
counted = res_mg.count
else:
summed += res_mg.sum
counted += res_mg.count
radial = res_mg.radial
res = Integrate1dResult(radial, summed/numpy.maximum(counted, 1e-10))
res._set_unit(res_mg.unit)
res._set_count(counted)
res._set_sum(summed)
return res
[63]:
multigonio = MultiGoniometer([goniometers[ds_names[i]] for i in range(9)],
["dist", "poni1", "poni2", "rot1", "offset"],
["scale", "nrj"])
[64]:
%time print(multigonio.chi2())
multigonio.param = numpy.array([ 7.20594053e-01, 3.22408604e-02, 4.05228023e-03, -2.75578440e-05,
-8.27999414e+01, 7.20612302e-01, 3.36369797e-02, 4.02094516e-03,
-1.74996556e-05, -7.71999791e+01, 7.20636130e-01, 3.47920978e-02,
4.01341931e-03, -1.21330600e-05, -7.15999090e+01, 7.20757808e-01,
3.33850817e-02, 3.95036100e-03, 3.46517345e-05, -6.57999267e+01,
7.20813915e-01, 3.22167822e-02, 3.97128822e-03, 2.00055269e-05,
-6.00000525e+01, 7.20881596e-01, 3.33801850e-02, 3.97760147e-03,
1.47074593e-05, -5.43998157e+01, 7.21048510e-01, 3.22346939e-02,
4.02104962e-03, -1.69519259e-05, -4.85998856e+01, 7.21074630e-01,
3.08484557e-02, 4.09385968e-03, -6.91378973e-05, -4.27999030e+01,
7.21154891e-01, 3.20619921e-02, 4.24950906e-03, -1.81328256e-04,
-3.71999987e+01, 9.99038595e-01, 1.70266104e+01])
%time print(multigonio.chi2())
8.603024734828662e-09
CPU times: user 357 ms, sys: 15.9 ms, total: 373 ms
Wall time: 371 ms
6.139505955765795e-09
CPU times: user 308 ms, sys: 16 ms, total: 324 ms
Wall time: 323 ms
[65]:
%time multigonio.refine2()
Cost function before refinement: 6.139505955765795e-09
[ 7.20594053e-01 3.22408604e-02 4.05228023e-03 -2.75578440e-05
-8.27999414e+01 7.20612302e-01 3.36369797e-02 4.02094516e-03
-1.74996556e-05 -7.71999791e+01 7.20636130e-01 3.47920978e-02
4.01341931e-03 -1.21330600e-05 -7.15999090e+01 7.20757808e-01
3.33850817e-02 3.95036100e-03 3.46517345e-05 -6.57999267e+01
7.20813915e-01 3.22167822e-02 3.97128822e-03 2.00055269e-05
-6.00000525e+01 7.20881596e-01 3.33801850e-02 3.97760147e-03
1.47074593e-05 -5.43998157e+01 7.21048510e-01 3.22346939e-02
4.02104962e-03 -1.69519259e-05 -4.85998856e+01 7.21074630e-01
3.08484557e-02 4.09385968e-03 -6.91378973e-05 -4.27999030e+01
7.21154891e-01 3.20619921e-02 4.24950906e-03 -1.81328256e-04
-3.71999987e+01 9.99038595e-01 1.70266104e+01]
message: Optimization terminated successfully
success: True
status: 0
fun: 6.139505955765795e-09
x: [ 7.206e-01 3.224e-02 ... 9.990e-01 1.703e+01]
nit: 1
jac: [ 5.910e-08 -8.339e-08 ... -4.210e-08 6.458e-07]
nfev: 48
njev: 1
Cost function after refinement: 6.139505955765795e-09
CPU times: user 16 s, sys: 360 ms, total: 16.4 s
Wall time: 16.4 s
[65]:
array([ 7.20594053e-01, 3.22408604e-02, 4.05228023e-03, -2.75578440e-05,
-8.27999414e+01, 7.20612302e-01, 3.36369797e-02, 4.02094516e-03,
-1.74996556e-05, -7.71999791e+01, 7.20636130e-01, 3.47920978e-02,
4.01341931e-03, -1.21330600e-05, -7.15999090e+01, 7.20757808e-01,
3.33850817e-02, 3.95036100e-03, 3.46517345e-05, -6.57999267e+01,
7.20813915e-01, 3.22167822e-02, 3.97128822e-03, 2.00055269e-05,
-6.00000525e+01, 7.20881596e-01, 3.33801850e-02, 3.97760147e-03,
1.47074593e-05, -5.43998157e+01, 7.21048510e-01, 3.22346939e-02,
4.02104962e-03, -1.69519259e-05, -4.85998856e+01, 7.21074630e-01,
3.08484557e-02, 4.09385968e-03, -6.91378973e-05, -4.27999030e+01,
7.21154891e-01, 3.20619921e-02, 4.24950906e-03, -1.81328256e-04,
-3.71999987e+01, 9.99038595e-01, 1.70266104e+01])
[66]:
LaB6_new = get_calibrant("LaB6")
LaB6_new.wavelength = 1e-10*hc/multigonio.param[-1]
print(LaB6,"\n", LaB6_new)
LaB6 Calibrant with 109 reflections at wavelength 7.281789822635113e-11
LaB6 Calibrant with 109 reflections at wavelength 7.281789829007909e-11
[67]:
%time res = multigonio.integrate([data[ds_names[i]] for i in range(9)])
[ 7.20594053e-01 3.22408604e-02 4.05228023e-03 -2.75578440e-05
-8.27999414e+01 9.99038595e-01 1.70266104e+01]
[ 7.20612302e-01 3.36369797e-02 4.02094516e-03 -1.74996556e-05
-7.71999791e+01 9.99038595e-01 1.70266104e+01]
[ 7.20636130e-01 3.47920978e-02 4.01341931e-03 -1.21330600e-05
-7.15999090e+01 9.99038595e-01 1.70266104e+01]
[ 7.20757808e-01 3.33850817e-02 3.95036100e-03 3.46517345e-05
-6.57999267e+01 9.99038595e-01 1.70266104e+01]
[ 7.20813915e-01 3.22167822e-02 3.97128822e-03 2.00055269e-05
-6.00000525e+01 9.99038595e-01 1.70266104e+01]
[ 7.20881596e-01 3.33801850e-02 3.97760147e-03 1.47074593e-05
-5.43998157e+01 9.99038595e-01 1.70266104e+01]
[ 7.21048510e-01 3.22346939e-02 4.02104962e-03 -1.69519259e-05
-4.85998856e+01 9.99038595e-01 1.70266104e+01]
[ 7.21074630e-01 3.08484557e-02 4.09385968e-03 -6.91378973e-05
-4.27999030e+01 9.99038595e-01 1.70266104e+01]
[ 7.21154891e-01 3.20619921e-02 4.24950906e-03 -1.81328256e-04
-3.71999987e+01 9.99038595e-01 1.70266104e+01]
CPU times: user 11.8 s, sys: 13.5 s, total: 25.4 s
Wall time: 6.44 s
[68]:
ax = jupyter.plot1d(res, calibrant=LaB6_new)
ax.figure.show()
/tmp/ipykernel_367778/1083240546.py:2: UserWarning: Matplotlib is currently using module://matplotlib_inline.backend_inline, which is a non-GUI backend, so cannot show the figure.
ax.figure.show()
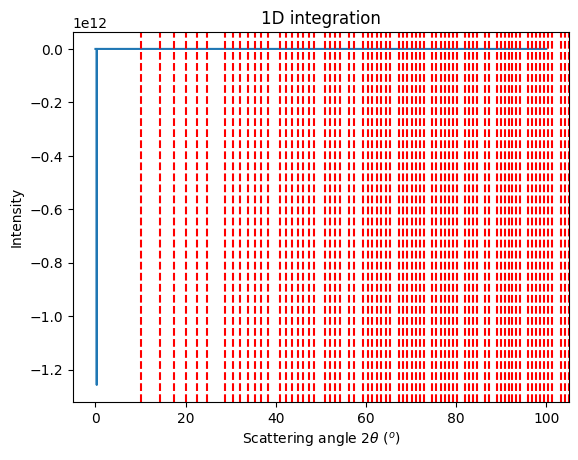
[69]:
fig, ax = plt.subplots()
ax.plot(*calc_fwhm(res, LaB6_new, 10, 95), "o", label="FWHM")
ax.plot(*calc_peak_error(res, LaB6_new, 10, 95), "o", label="error")
ax.set_title("Peak shape & error as function of the angle")
ax.set_xlabel(res.unit.label)
ax.legend()
fig.show()
28454
68 60
/tmp/ipykernel_367778/344732789.py:7: UserWarning: Matplotlib is currently using module://matplotlib_inline.backend_inline, which is a non-GUI backend, so cannot show the figure.
fig.show()
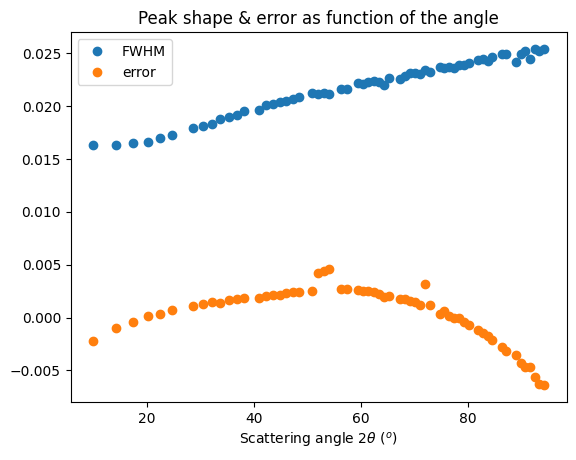
[70]:
print("total run time: ", time.time()-start_time)
total run time: 1055.6983478069305
Conclusion
The calibration works and the FWHM of every single peak is pretty small: 0.02°. The geometry has been refined with the wavelength: The goniometer scale parameter refines to 0.999 instead of 1 and the wavelength is fitted with a change at the 5th digit which is pretty precise.