Inpainting missing data
Missing data in an image can be an issue, especially when one wants to perform Fourier analysis. This tutorial explains how to fill-up missing pixels with values which looks “realistic” and introduce as little perturbation as possible for subsequent analysis. The user should keep the mask nearby and only consider the values of actual pixels and never the one inpainted.
This tutorial will use fully synthetic data to allow comparison between actual (syntetic) data with inpainted values.
The first part of the tutorial is about the generation of a challenging 2D diffraction image with realistic noise and to describe the metric used, then comes the actual tutorial on how to use the inpainting. Finally a benchmark is used based on the metric determined.
Creation of the image
A realistic challenging image should contain:
Bragg peak rings. We chose LaB6 as guinea-pig, with very sharp peaks, at the limit of the resolution of the detector
Some amorphous content
strong polarization effect
Poissonian noise
One image will be generated but then multiple ones with different noise to discriminate the effect of the noise from other effects.
[1]:
%matplotlib inline
# Used for documentation to inline plots into notebook
# %matplotlib widget
# uncomment the later for better UI
from matplotlib.pyplot import subplots
import numpy
[2]:
import pyFAI
print("Using pyFAI version: ", pyFAI.version)
from pyFAI.azimuthalIntegrator import AzimuthalIntegrator
from pyFAI.gui import jupyter
import pyFAI.test.utilstest
from pyFAI.calibrant import get_calibrant
import time
start_time = time.perf_counter()
Using pyFAI version: 2024.9.0-dev0
[3]:
detector = pyFAI.detector_factory("Pilatus2MCdTe")
mask = detector.mask.copy()
nomask = numpy.zeros_like(mask)
detector.mask=nomask
ai = AzimuthalIntegrator(detector=detector)
ai.setFit2D(200, 200, 200)
ai.wavelength = 3e-11
print(ai)
Detector Pilatus CdTe 2M PixelSize= 172µm, 172µm BottomRight (3)
Wavelength= 3.000000e-11 m
SampleDetDist= 2.000000e-01 m PONI= 3.440000e-02, 3.440000e-02 m rot1=0.000000 rot2=0.000000 rot3=0.000000 rad
DirectBeamDist= 200.000 mm Center: x=200.000, y=200.000 pix Tilt= 0.000° tiltPlanRotation= 0.000° 𝛌= 0.300Å
[4]:
LaB6 = get_calibrant("LaB6")
LaB6.wavelength = ai.wavelength
print(LaB6)
r = ai.array_from_unit(unit="q_nm^-1")
decay_b = numpy.exp(-(r-50)**2/2000)
bragg = LaB6.fake_calibration_image(ai, Imax=1e4, W=1e-6) * ai.polarization(factor=1.0) * decay_b
decay_a = numpy.exp(-r/100)
amorphous = 1000*ai.polarization(factor=1.0)*ai.solidAngleArray() * decay_a
img_nomask = bragg + amorphous
#Not the same noise function for all images two images
img_nomask = numpy.random.poisson(img_nomask)
img_nomask2 = numpy.random.poisson(img_nomask)
img = numpy.random.poisson(img_nomask)
img[numpy.where(mask)] = -1
fig,ax = subplots(1,2, figsize=(10,5))
jupyter.display(img=img, label="With mask", ax=ax[0])
jupyter.display(img=img_nomask, label="Without mask", ax=ax[1])
LaB6 Calibrant with 640 reflections at wavelength 3e-11
[4]:
<Axes: title={'center': 'Without mask'}>
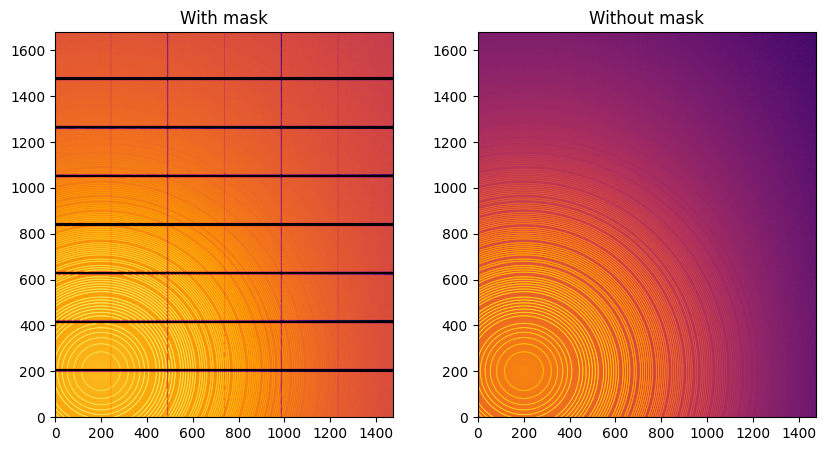
Note the aliassing effect on the displayed images.
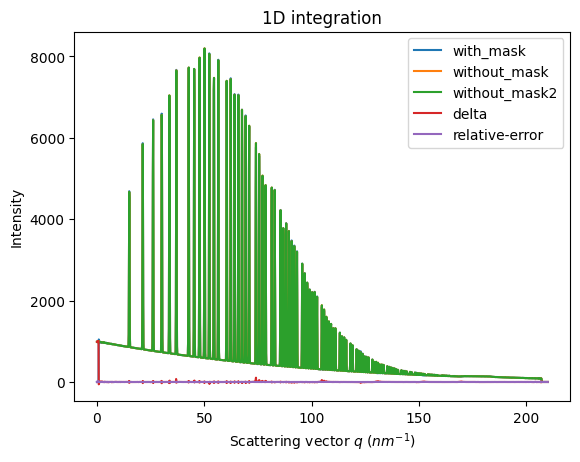
We will measure now the effect after 1D intergeration. We do not correct for polarization on purpose to highlight the defect one wishes to whipe out. We use a R-factor to describe the quality of the 1D-integrated signal.
[5]:
wo = ai.integrate1d(img_nomask, 2000, unit="q_nm^-1", method="splitpixel", radial_range=(0,210))
wo2 = ai.integrate1d(img_nomask2, 2000, unit="q_nm^-1", method="splitpixel", radial_range=(0,210))
wm = ai.integrate1d(img, 2000, unit="q_nm^-1", method="splitpixel", mask=mask, radial_range=(0,210))
ax = jupyter.plot1d(wm , label="with_mask")
ax.plot(*wo, label="without_mask")
ax.plot(*wo2, label="without_mask2")
ax.plot(wo.radial, wo.intensity-wm.intensity, label="delta")
ax.plot(wo.radial, wo.intensity-wo2.intensity, label="relative-error")
ax.legend()
print("Between masked and non masked image R= %s"%pyFAI.utils.mathutil.rwp(wm,wo))
print("Between two different non-masked images R'= %s"%pyFAI.utils.mathutil.rwp(wo2,wo))
Between masked and non masked image R= 5.67700904372284
Between two different non-masked images R'= 0.22219246808262047
[6]:
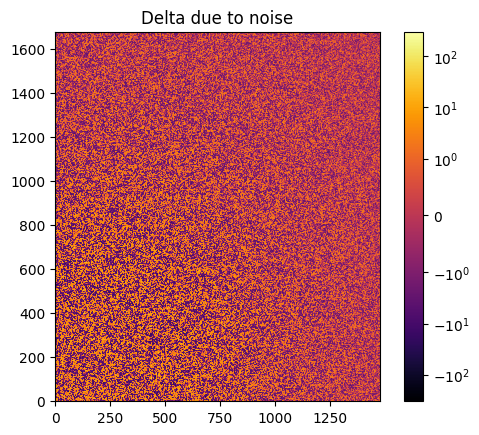
# Effect of the noise on the delta image
fig, ax = subplots()
jupyter.display(img=img_nomask-img_nomask2, label="Delta due to noise", ax=ax)
ax.figure.colorbar(ax.images[0])
[6]:
<matplotlib.colorbar.Colorbar at 0x7f1c9034e380>
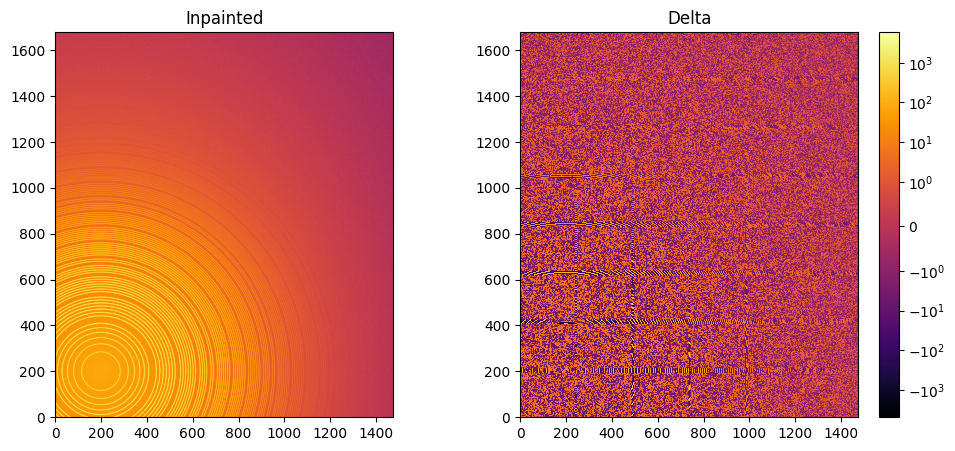
Inpainting
This part describes how to paint the missing pixels for having a “natural-looking image”. The delta image contains the difference with the original image
[7]:
#Inpainting:
inpainted = ai.inpainting(img, mask=mask, poissonian=True)
fig, ax = subplots(1, 2, figsize=(12,5))
jupyter.display(img=inpainted, label="Inpainted", ax=ax[0])
jupyter.display(img=img_nomask-inpainted, label="Delta", ax=ax[1])
ax[1].figure.colorbar(ax[1].images[0])
[7]:
<matplotlib.colorbar.Colorbar at 0x7f1c9011ec20>
[8]:
# Comparison of the inpained image with the original one:
wm = ai.integrate1d(inpainted, 2000, unit="q_nm^-1", method="splitpixel", radial_range=(0,210))
wo = ai.integrate1d(img_nomask, 2000, unit="q_nm^-1", method="splitpixel", radial_range=(0,210))
ax = jupyter.plot1d(wm , label="inpainted")
ax.plot(*wo, label="without_mask")
ax.plot(wo.radial, wo.intensity-wm.intensity, label="delta")
ax.legend()
print("R= %s"%pyFAI.utils.mathutil.rwp(wm,wo))
R= 1.2671014289898865
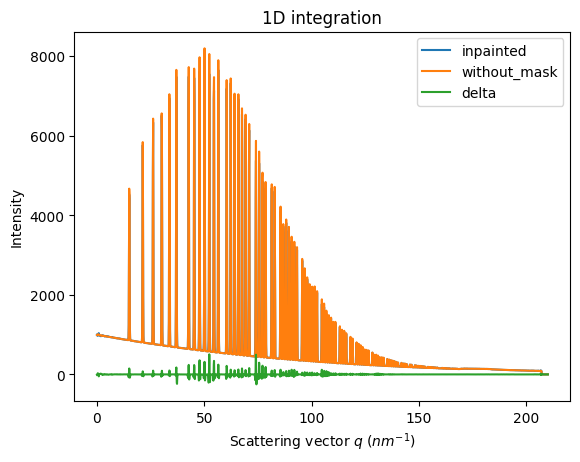
One can see by zooming in that the main effect on inpainting is a broadening of the signal in the inpainted region. This could (partially) be adressed by increasing the number of radial bins used in the inpainting.
Benchmarking and optimization of the parameters
The parameter set depends on the detector, the experiment geometry and the type of signal on the detector. Finer detail require finer slicing.
[9]:
#Basic benchmarking of execution time for default options:
%timeit inpainted = ai.inpainting(img, mask=mask)
2.35 s ± 14.1 ms per loop (mean ± std. dev. of 7 runs, 1 loop each)
[10]:
wo = ai.integrate1d(img_nomask, 2000, unit="q_nm^-1", method="splitpixel", radial_range=(0,210))
for m in (("no", "histogram", "cython"), ("bbox", "histogram","cython")):
for k in (512, 1024, 2048, 4096):
ai.reset()
for i in (0, 1, 2, 4, 8):
inpainted = ai.inpainting(img, mask=mask, poissonian=True, method=m, npt_rad=k, grow_mask=i)
wm = ai.integrate1d(inpainted, 2000, unit="q_nm^-1", method="splitpixel", radial_range=(0,210))
print(f"method: {m} npt_rad={k} grow={i}; R= {pyFAI.utils.mathutil.rwp(wm,wo)}")
method: ('no', 'histogram', 'cython') npt_rad=512 grow=0; R= 7.844445218847064
method: ('no', 'histogram', 'cython') npt_rad=512 grow=1; R= 7.842974458398813
method: ('no', 'histogram', 'cython') npt_rad=512 grow=2; R= 7.844231843551052
method: ('no', 'histogram', 'cython') npt_rad=512 grow=4; R= 7.8459067065616805
method: ('no', 'histogram', 'cython') npt_rad=512 grow=8; R= 7.843799959988562
method: ('no', 'histogram', 'cython') npt_rad=1024 grow=0; R= 8.08869312385723
method: ('no', 'histogram', 'cython') npt_rad=1024 grow=1; R= 8.089496973082857
method: ('no', 'histogram', 'cython') npt_rad=1024 grow=2; R= 8.088952018044555
method: ('no', 'histogram', 'cython') npt_rad=1024 grow=4; R= 8.089811534346834
method: ('no', 'histogram', 'cython') npt_rad=1024 grow=8; R= 8.089758764616912
method: ('no', 'histogram', 'cython') npt_rad=2048 grow=0; R= 8.209181321569549
method: ('no', 'histogram', 'cython') npt_rad=2048 grow=1; R= 8.209377516243512
method: ('no', 'histogram', 'cython') npt_rad=2048 grow=2; R= 8.209665288295193
method: ('no', 'histogram', 'cython') npt_rad=2048 grow=4; R= 8.209180180783662
method: ('no', 'histogram', 'cython') npt_rad=2048 grow=8; R= 8.209283935325205
method: ('no', 'histogram', 'cython') npt_rad=4096 grow=0; R= 8.284407434407044
method: ('no', 'histogram', 'cython') npt_rad=4096 grow=1; R= 8.284709934058238
method: ('no', 'histogram', 'cython') npt_rad=4096 grow=2; R= 8.284544117976838
method: ('no', 'histogram', 'cython') npt_rad=4096 grow=4; R= 8.28433285781612
method: ('no', 'histogram', 'cython') npt_rad=4096 grow=8; R= 8.284431414086317
method: ('bbox', 'histogram', 'cython') npt_rad=512 grow=0; R= 3.1669197218113028
method: ('bbox', 'histogram', 'cython') npt_rad=512 grow=1; R= 2.9086240608760185
method: ('bbox', 'histogram', 'cython') npt_rad=512 grow=2; R= 2.7124282408093987
method: ('bbox', 'histogram', 'cython') npt_rad=512 grow=4; R= 2.625591801847571
method: ('bbox', 'histogram', 'cython') npt_rad=512 grow=8; R= 2.5446556740325796
method: ('bbox', 'histogram', 'cython') npt_rad=1024 grow=0; R= 1.6899530791526276
method: ('bbox', 'histogram', 'cython') npt_rad=1024 grow=1; R= 1.3293008844632694
method: ('bbox', 'histogram', 'cython') npt_rad=1024 grow=2; R= 1.3255138047195456
method: ('bbox', 'histogram', 'cython') npt_rad=1024 grow=4; R= 1.2840494293434288
method: ('bbox', 'histogram', 'cython') npt_rad=1024 grow=8; R= 1.2801822774443288
method: ('bbox', 'histogram', 'cython') npt_rad=2048 grow=0; R= 0.9132723431368797
method: ('bbox', 'histogram', 'cython') npt_rad=2048 grow=1; R= 0.6742151534405462
method: ('bbox', 'histogram', 'cython') npt_rad=2048 grow=2; R= 0.6570017077412936
method: ('bbox', 'histogram', 'cython') npt_rad=2048 grow=4; R= 0.6527608355153538
method: ('bbox', 'histogram', 'cython') npt_rad=2048 grow=8; R= 0.6560476366091916
method: ('bbox', 'histogram', 'cython') npt_rad=4096 grow=0; R= 0.5887728253881461
method: ('bbox', 'histogram', 'cython') npt_rad=4096 grow=1; R= 0.4481847349331564
method: ('bbox', 'histogram', 'cython') npt_rad=4096 grow=2; R= 0.45249276572979896
method: ('bbox', 'histogram', 'cython') npt_rad=4096 grow=4; R= 0.4447540207481813
method: ('bbox', 'histogram', 'cython') npt_rad=4096 grow=8; R= 0.44827575042027507
[11]:
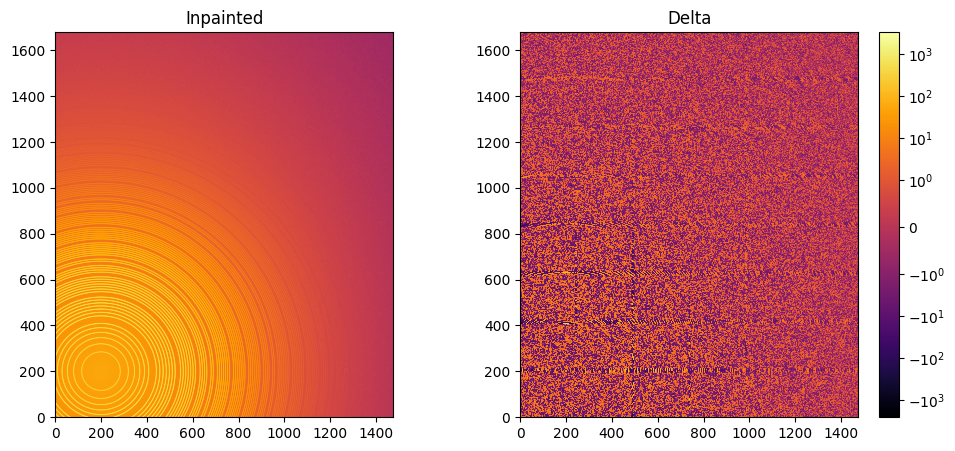
#Inpainting, best solution found:
ai.reset()
%time inpainted = ai.inpainting(img, mask=mask, poissonian=True, method=("pseudo", "csr", "cython"), npt_rad=4096, grow_mask=1)
fig, ax = subplots(1, 2, figsize=(12, 5))
jupyter.display(img=inpainted, label="Inpainted", ax=ax[0])
jupyter.display(img=img_nomask-inpainted, label="Delta", ax=ax[1])
ax[1].figure.colorbar(ax[1].images[0])
pass
CPU times: user 3.41 s, sys: 454 ms, total: 3.86 s
Wall time: 3.26 s
[12]:
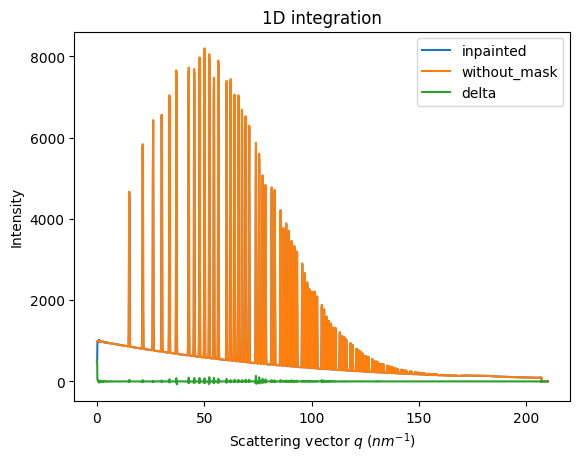
# Comparison of the inpained image with the original one:
wm = ai.integrate1d(inpainted, 2000, unit="q_nm^-1", method="splitpixel", radial_range=(0,210))
wo = ai.integrate1d(img_nomask, 2000, unit="q_nm^-1", method="splitpixel", radial_range=(0,210))
ax = jupyter.plot1d(wm , label="inpainted")
ax.plot(*wo, label="without_mask")
ax.plot(wo.radial, wo.intensity-wm.intensity, label="delta")
ax.legend()
print("R= %s"%pyFAI.utils.mathutil.rwp(wm,wo))
R= 0.9929187811170841
Conclusion
Inpainting is one of the only solution to fill up the gaps in detector when Fourier analysis is needed. This tutorial explains basically how this is possible using the pyFAI library and how to optimize the parameter set for inpainting. The result may greatly vary with detector position and tilt and the kind of signal (amorphous or more spotty).
[13]:
print(f"Execution time: {time.perf_counter()-start_time:.3f} s")
Execution time: 77.365 s