Calibration of the pixel position for a Pilatus detector

This tutorial summarizes the work done by Frederic Sulzman during his internship at ESRF during the summer 2015 entilted “Calibration for geometric distortion in multi- modules pixel detectors”.

The overall strategy is very similar to “CCD calibration” tutorial with some specificities due to the modular nature of the detector.

0. Image preprocessing

1. Peak picking

2. Grid assignment

3. Displacement fitting

4. Reconstruction of the pixel position

5. Saving into a detector definition file

6. Validation of the geometry with a 2D integration

Each module being made by lithographic processes, the error within a module will be assumeed to be constant. We will use the name “displacement of the module” to describe the rigide movement of the module.

This tutorial uses data from the Pilatus3 2M CdTe from the ID15 beam line of the ESRF. They provided not only the intersnip subject but also the couple of images uses to calibrate the detector.

This detector contains 48 half-modules, each bound to a single CdTe monocrystal sensor and is designed for high energy X-ray radiation detection. Due to the construction procedure, these half-modules could show a misalignment within the detector plane. While the manufacturer (Dectris) garanties a precision within a pixel (172µm), the miss-alignment of certain modules can be seen while calibrating Debye-Scherrer ring using refereance sample. So the aim of this work is to provide a detector description with a better precision better than the original detector.

This work will be performed on the image of a grid available: http://www.silx.org/pub/pyFAI/detector_calibration/Pilatus2MCdTe_ID15_grid_plus_sample_0004.cbf and the scattering of ceria (CeO2) at 72.1keV available here. http://www.silx.org/pub/pyFAI/detector_calibration/Pilatus2MCdTe_ID15_CeO2_72100eV_800mm_0000.cbf

It is a good exercise to calibrate all rings of the later image using the pyFAI-calib2 tool. A calibration close to perfection is needed to visualize the module miss-alignement we aim at correcting.

%matplotlib inline
#For documentation purpose, `inline` is used to enforce the storage of the image in the notebook
#matplotlib widget
#many imports which will be used all along the notebook
import time
start_time = time.perf_counter()
import os
import pyFAI
import fabio
import glob
import numpy
from numpy.lib.stride_tricks import as_strided
from math import sin, cos, sqrt
from scipy.ndimage import convolve, binary_dilation
from scipy.spatial import distance_matrix
from scipy.optimize import minimize
from matplotlib.pyplot import subplots
from pyFAI.ext.bilinear import Bilinear
from pyFAI.ext.watershed import InverseWatershed
from silx.resources import ExternalResources
from pyFAI.azimuthalIntegrator import AzimuthalIntegrator

# A couple of compound dtypes ...
dt = numpy.dtype([('y', numpy.float64),
                  ('x', numpy.float64),
                  ('i', numpy.int64),
                 ])
dl = numpy.dtype([('y', numpy.float64),
                  ('x', numpy.float64),
                  ('i', numpy.int64),
                  ('Y', numpy.int64),
                  ('X', numpy.int64),
                 ])

print("Using pyFAI verison: ", pyFAI.version)

Using pyFAI verison:  2024.9.0-dev0

#Nota: Configure here your proxy if you are behind a firewall
#os.environ["http_proxy"] = "http://proxy.comany.com:3128"

downloader = ExternalResources("detector_calibration", "http://www.silx.org/pub/pyFAI/detector_calibration/")
ring_file = downloader.getfile("Pilatus2MCdTe_ID15_CeO2_72100eV_800mm_0000.cbf")
print(ring_file)
grid_file = downloader.getfile("Pilatus2MCdTe_ID15_grid_plus_sample_0004.cbf")
print(grid_file)

/tmp/detector_calibration_testdata_edgar1993a/Pilatus2MCdTe_ID15_CeO2_72100eV_800mm_0000.cbf
/tmp/detector_calibration_testdata_edgar1993a/Pilatus2MCdTe_ID15_grid_plus_sample_0004.cbf

rings = fabio.open(ring_file).data
img = fabio.open(grid_file).data
fig,ax = subplots(1,2, figsize=(10,5))
ax[0].imshow(img.clip(0,1000), interpolation="bilinear")
ax[0].set_title("grid")
ax[1].imshow(numpy.arcsinh(rings), interpolation="bilinear")
ax[1].set_title("rings")
pass

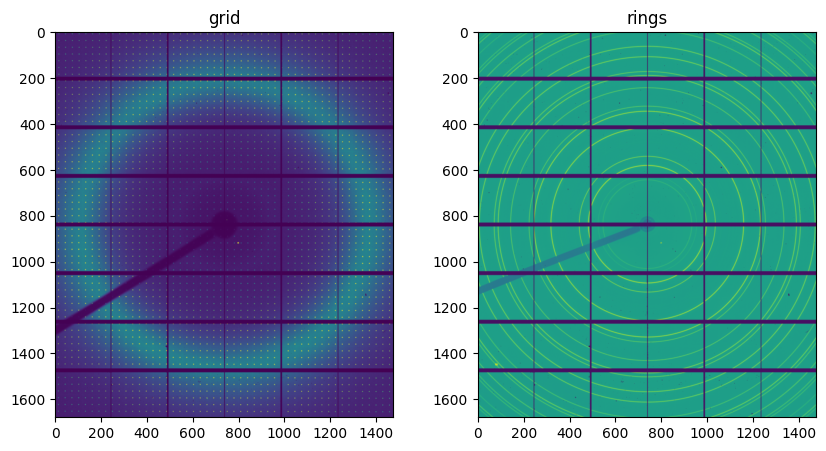
Image processing

There are 3 pre-processing steps which are needed.

1. Define for each module a unique identifier which will be used later on during the fitting procedure

2. Define the proper mask: each module is the assembly of 4x2 sub-modules and there are (3) interpolated pixels between each sub-module, such “unreliable pixels should be masked out as well

3. Correct the grid image by the smoothed image to have a constant background.

4. Convolve the raw image with a typical hole shape to allow a precise spotting of the hole center.

# This is the default detector as definied in pyFAI according to the specification provided by Dectris:
pilatus = pyFAI.detector_factory("Pilatus_2m_CdTe")
print(pilatus)

mask1 = pilatus.mask
module_size = pilatus.MODULE_SIZE
module_gap = pilatus.MODULE_GAP
submodule_size = (96,60)

Detector Pilatus CdTe 2M         PixelSize= 172µm, 172µm         BottomRight (3)

#1 + 2 Calculation of the module_id and the interpolated-mask:
mid = numpy.zeros(pilatus.shape, dtype=int)
mask2 = numpy.zeros(pilatus.shape, dtype=int)
idx = 1
for i in range(8):
    y_start = i*(module_gap[0] + module_size[0])
    y_stop = y_start + module_size[0]
    for j in range(3):
        x_start = j*(module_gap[1] + module_size[1])
        x_stop = x_start + module_size[1]
        mid[y_start:y_stop,x_start: x_start+module_size[1]//2] = idx
        idx+=1
        mid[y_start:y_stop,x_start+module_size[1]//2: x_stop] = idx
        idx+=1
        mask2[y_start+submodule_size[0]-1:y_start+submodule_size[0]+2,
              x_start:x_stop] = 1
        for k in range(1,8):
            mask2[y_start:y_stop,
              x_start+k*(submodule_size[1]+1)-1:x_start+k*(submodule_size[1]+1)+2] = 1

#Extra masking
mask0 = img<0
#Those pixel are miss-behaving... they are the hot pixels next to the beam-stop
mask0[915:922,793:800] = 1
mask0[817:820,747:750] = 1

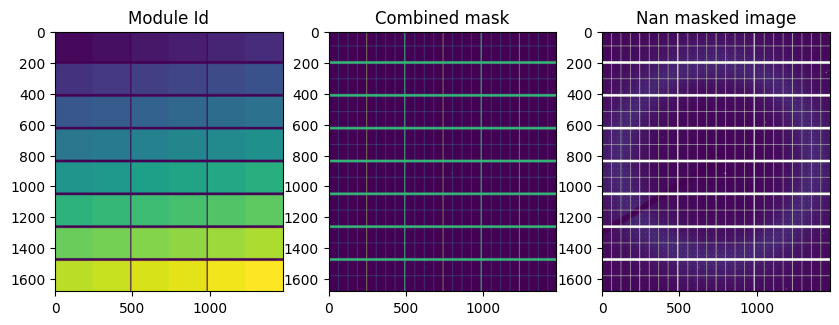
fig,ax = subplots(1,3, figsize=(10,4))
ax[0].imshow(mid, interpolation="bilinear")
ax[0].set_title("Module Id")

ax[1].imshow(mask2+mask1+mask0, interpolation="bilinear")
ax[1].set_title("Combined mask")

nimg = img.astype(float)
nimg[numpy.where(mask0+mask1+mask2)] = numpy.nan


ax[2].imshow(nimg)#, interpolation="bilinear")
ax[2].set_title("Nan masked image")
pass

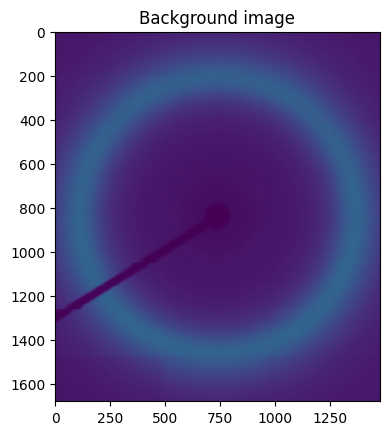
# The Nan-masked image contains now only valid values (and Nan elsewhere). We will make a large median filter to
# build up a smooth image without gaps.
#
# This function is backported from future version of numpy ... it allows to expose a winbowed view
# to perform the nanmedian-filter

def sliding_window_view(x, shape, subok=False, readonly=True):
    """
    Creates sliding window views of the N dimensional array with the given window
    shape. Window slides across each dimension of `x` and extract subsets of `x`
    at any window position.
    Parameters
    ----------
    x : array_like
        Array to create sliding window views of.
    shape : sequence of int
        The shape of the window. Must have same length as the number of input array dimensions.
    subok : bool, optional
        If True, then sub-classes will be passed-through, otherwise the returned
        array will be forced to be a base-class array (default).
    readonly : bool, optional
        If set to True, the returned array will always be readonly view.
        Otherwise it will return writable copies(see Notes).
    Returns
    -------
    view : ndarray
        Sliding window views (or copies) of `x`. view.shape = x.shape - shape + 1
    See also
    --------
    as_strided: Create a view into the array with the given shape and strides.
    broadcast_to: broadcast an array to a given shape.
    Notes
    -----
    ``sliding_window_view`` create sliding window views of the N dimensions array
    with the given window shape and its implementation based on ``as_strided``.
    Please note that if readonly set to True, views are returned, not copies
    of array. In this case, write operations could be unpredictable, so the returned
    views are readonly. Bear in mind that returned copies (readonly=False) will
    take more memory than the original array, due to overlapping windows.
    For some cases there may be more efficient approaches to calculate transformations
    across multi-dimensional arrays, for instance `scipy.signal.fftconvolve`, where combining
    the iterating step with the calculation itself while storing partial results can result
    in significant speedups.
    Examples
    --------
    >>> i, j = np.ogrid[:3,:4]
    >>> x = 10*i + j
    >>> shape = (2,2)
    >>> np.lib.stride_tricks.sliding_window_view(x, shape)
    array([[[[ 0,  1],
             [10, 11]],
            [[ 1,  2],
             [11, 12]],
            [[ 2,  3],
             [12, 13]]],
           [[[10, 11],
             [20, 21]],
            [[11, 12],
             [21, 22]],
            [[12, 13],
             [22, 23]]]])
    """
    np = numpy
    # first convert input to array, possibly keeping subclass
    x = np.array(x, copy=False, subok=subok)

    try:
        shape = np.array(shape, dtype=np.int64)
    except:
        raise TypeError('`shape` must be a sequence of integer')
    else:
        if shape.ndim > 1:
            raise ValueError('`shape` must be one-dimensional sequence of integer')
        if len(x.shape) != len(shape):
            raise ValueError("`shape` length doesn't match with input array dimensions")
        if np.any(shape <= 0):
            raise ValueError('`shape` cannot contain non-positive value')

    o = np.array(x.shape) - shape  + 1 # output shape
    if np.any(o <= 0):
        raise ValueError('window shape cannot larger than input array shape')

    if type(readonly) != bool:
        raise TypeError('readonly must be a boolean')

    strides = x.strides
    view_strides = strides

    view_shape = np.concatenate((o, shape), axis=0)
    view_strides = np.concatenate((view_strides, strides), axis=0)
    view = as_strided(x, view_shape, view_strides, subok=subok, writeable=not readonly)

    if not readonly:
        return view.copy()
    else:
        return view

%%time
#Calculate a background image using a large median filter ... takes a while
shape = (19,11)
print(nimg.shape)
padded = numpy.pad(nimg, tuple((i//2,) for i in shape), mode="edge")
print(padded.shape)
background = numpy.nanmedian(sliding_window_view(padded, shape), axis = (-2,-1))
print(background.shape)
fig,ax = subplots()
ax.imshow(background)
ax.set_title("Background image")
pass

(1679, 1475)
(1697, 1485)
(1679, 1475)
CPU times: user 22.9 s, sys: 20.4 s, total: 43.4 s
Wall time: 43.7 s

fig,ax = subplots(1,2, figsize=(9,5))

normalized = (nimg/background)

low = numpy.nanmin(normalized)
high = numpy.nanmax(normalized)
print(low, high)
normalized[numpy.isnan(normalized)] = 0
normalized /= high

ax[0].imshow(normalized)
ax[0].set_title("Normalized image")

ax[1].hist(normalized.ravel(), 100, range=(0,1))
ax[1].set_title("Histogram of intensities in normalized image")
pass

0.0 17.728813559322035

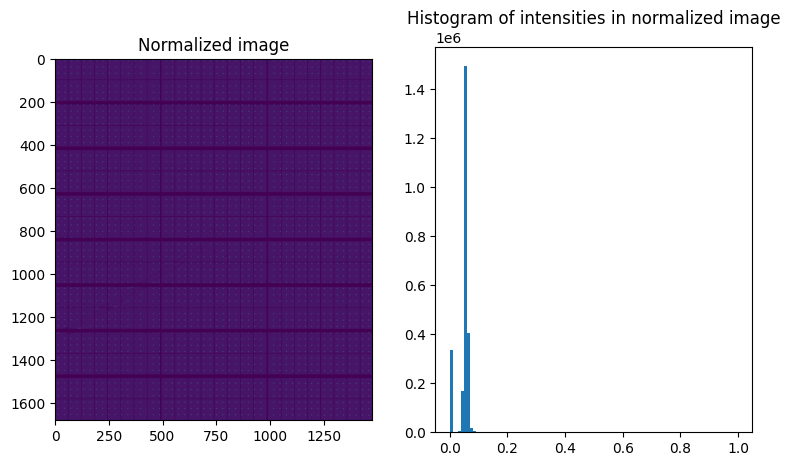
For a precise measurement of the peak position, one trick is to convolve the image with a pattern which looks like a hole of the grid.

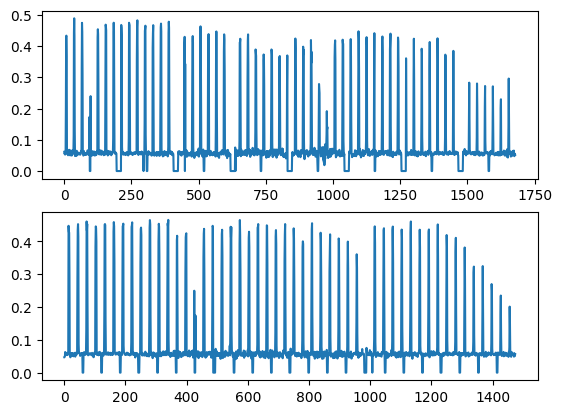
#print the profile of the normalized image: the center is difficult to measure due to the small size of the hole.
fig,ax = subplots(2)
ax[0].plot(normalized[:,545])
ax[1].plot(normalized[536,:])
pass

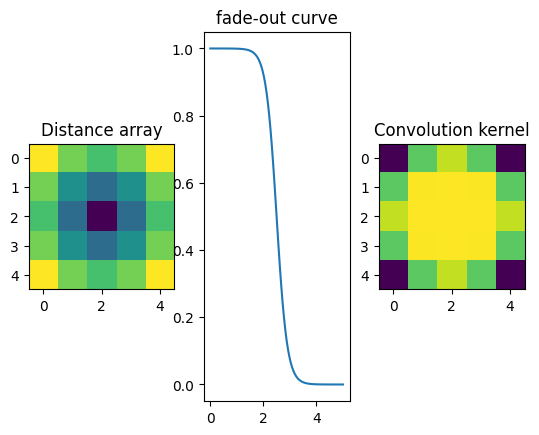
#Definition of the convolution kernel
ksize = 5
y,x = numpy.ogrid[-(ksize-1)//2:ksize//2+1,-(ksize-1)//2:ksize//2+1]
d = numpy.sqrt(y*y+x*x)

#Fade out curve definition
fadeout = lambda x: 1/(1+numpy.exp(5*(x-2.5)))

kernel = fadeout(d)
mini=kernel.sum()
print(mini)

fig,ax = subplots(1,3)
ax[0].imshow(d)
ax[0].set_title("Distance array")

ax[1].plot(numpy.linspace(0,5,100),fadeout(numpy.linspace(0,5,100)))
ax[1].set_title("fade-out curve")

ax[2].imshow(kernel)
ax[2].set_title("Convolution kernel")
pass

19.63857792789662

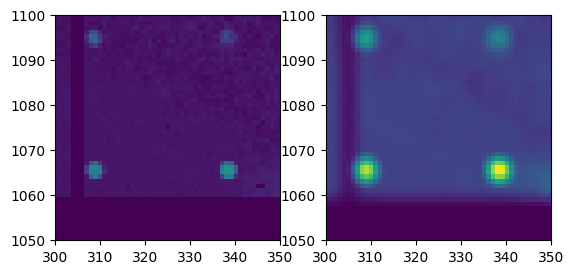
my_smooth = convolve(normalized, kernel, mode="constant", cval=0)/mini
print(my_smooth.shape)
fig,ax = subplots(1,2)
ax[0].imshow(normalized.clip(0,1))
ax[0].set_ylim(1050,1100)
ax[0].set_xlim(300,350)
ax[1].imshow(my_smooth.clip(0,1))
ax[1].set_ylim(1050,1100)
ax[1].set_xlim(300,350)
numpy.where(my_smooth == my_smooth.max())

(1679, 1475)

(array([1065]), array([338]))

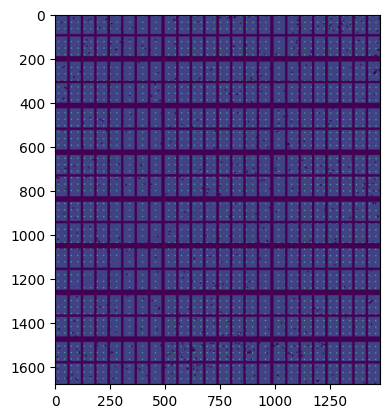
#mask out all pixels too close to any masked position

all_masks = numpy.logical_or(numpy.logical_or(mask0,mask1),mask2)
print(all_masks.sum())
big_mask = binary_dilation(all_masks, iterations=ksize//2+1+1)
print(big_mask.sum())
smooth2 = my_smooth.copy()
smooth2[big_mask] = 0
fig,ax = subplots()
ax.imshow(smooth2)
pass

335009
782371

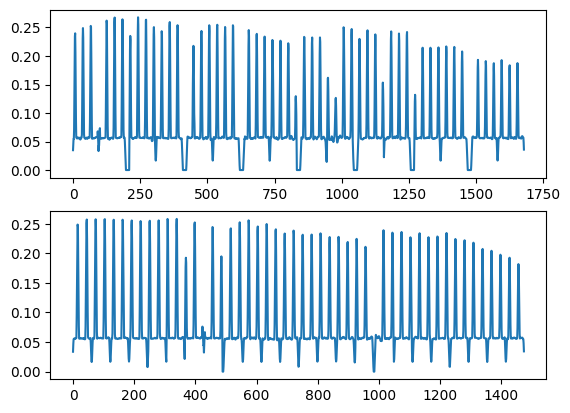
#Display the profile of the smoothed image: the center is easy to measure thanks to the smoothness of the signal
fig,ax = subplots(2)
ax[0].plot(my_smooth[:,545])
ax[1].plot(my_smooth[536,:])
pass

Peak picking

We use the watershed module from pyFAI to retrieve all peak positions. Those regions are sieved out respectively for:

• their size, it should be larger than the kernel itself

• the peaks too close to masked regions are removed

• the intensity of the peak

iw = InverseWatershed(my_smooth)
iw.init()
iw.merge_singleton()
all_regions = set(iw.regions.values())

regions = [i for i in all_regions if i.size>mini]

print("Number of region segmented: %s"%len(all_regions))
print("Number of large enough regions : %s"%len(regions))

Number of region segmented: 82126
Number of large enough regions : 41333

#Remove peaks on masked region
sieved_region = [i for i in regions if not big_mask[(i.index//nimg.shape[-1], i.index%nimg.shape[-1])]]
print("Number of peaks not on masked areea : %s"%len(sieved_region))

Number of peaks not on masked areea : 30001

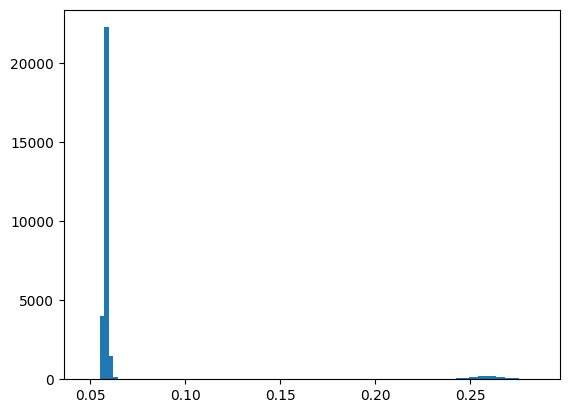
# Histogram of peak height:
s = numpy.array([i.maxi for i in sieved_region])

fig, ax = subplots()
ax.hist(s, 100)
pass

#sieve-out for peak intensity
int_mini = 0.1
peaks = [(i.index//nimg.shape[-1], i.index%nimg.shape[-1]) for i in sieved_region if (i.maxi)>int_mini]
print("Number of remaining peaks with I>%s: %s"%(int_mini, len(peaks)))

peaks_raw = numpy.array(peaks)

Number of remaining peaks with I>0.1: 2075

# Finally the peak positions are interpolated using a second order taylor expansion
# in thevinicy of the maximum value of the signal:

#Create bilinear interpolator
bl = Bilinear(my_smooth)

#Overlay raw peak coordinate and refined peak positions

ref_peaks = [bl.local_maxi(p) for p in peaks]
fig, ax = subplots()
ax.imshow(img.clip(0,1000), interpolation="nearest")
peaks_ref = numpy.array(ref_peaks)
ax.plot(peaks_raw[:,1], peaks_raw[:, 0], ".r")
ax.plot(peaks_ref[:,1],peaks_ref[:, 0], ".b")
ax.set_title("Extracted peak position (red: raw, blue: refined)")
print("Refined peak coordinate:")
print(ref_peaks[:10])

Refined peak coordinate:
[(742.1180413514376, 221.4319804608822), (743.4527280330658, 1309.30092304945), (743.4597269892693, 1338.5053663551807), (743.6080393493176, 1368.1613915711641), (743.5962627232075, 1397.376223564148), (743.7820372730494, 1427.0128736887127), (743.8194748610258, 1456.5655208230019), (742.3942741155624, 662.4384651482105), (596.40856808424, 1397.4448700249195), (596.4921390414238, 1426.6323048174381)]

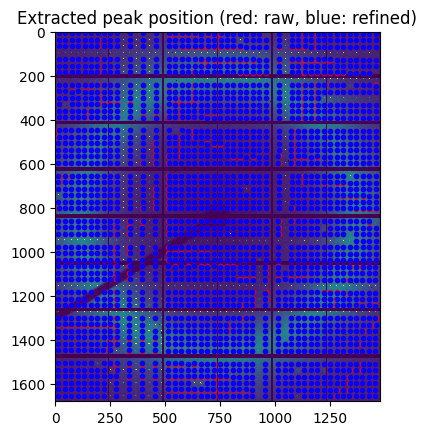
At this stage we have about 2000 peaks (with sub-pixel precision) which are visually distributed on all modules. Some modules have their peaks located along sub-module boundaries which are masked out, hence they have fewer ontrol point for the calculation. Let’s assign each peak to a module identifier. This allows to print out the number of peaks per module:

yxi = numpy.array([i+(mid[round(i[0]),round(i[1])],)
                   for i in ref_peaks], dtype=dt)
print("Number of keypoint per module:")
for i in range(1,mid.max()+1):
    print("Module id:",i, "cp:", (yxi[:]["i"] == i).sum())

Number of keypoint per module:
Module id: 1 cp: 48
Module id: 2 cp: 30
Module id: 3 cp: 48
Module id: 4 cp: 46
Module id: 5 cp: 42
Module id: 6 cp: 47
Module id: 7 cp: 47
Module id: 8 cp: 30
Module id: 9 cp: 48
Module id: 10 cp: 48
Module id: 11 cp: 41
Module id: 12 cp: 39
Module id: 13 cp: 48
Module id: 14 cp: 30
Module id: 15 cp: 47
Module id: 16 cp: 48
Module id: 17 cp: 42
Module id: 18 cp: 48
Module id: 19 cp: 47
Module id: 20 cp: 30
Module id: 21 cp: 48
Module id: 22 cp: 47
Module id: 23 cp: 42
Module id: 24 cp: 47
Module id: 25 cp: 48
Module id: 26 cp: 30
Module id: 27 cp: 48
Module id: 28 cp: 47
Module id: 29 cp: 41
Module id: 30 cp: 50
Module id: 31 cp: 46
Module id: 32 cp: 30
Module id: 33 cp: 48
Module id: 34 cp: 42
Module id: 35 cp: 47
Module id: 36 cp: 48
Module id: 37 cp: 48
Module id: 38 cp: 28
Module id: 39 cp: 48
Module id: 40 cp: 42
Module id: 41 cp: 44
Module id: 42 cp: 48
Module id: 43 cp: 47
Module id: 44 cp: 26
Module id: 45 cp: 46
Module id: 46 cp: 42
Module id: 47 cp: 45
Module id: 48 cp: 48

Grid assignment

The calibration is performed using a regular grid, the idea is to assign to each peak of coordinates (x,y) the integer value (X, Y) which correspond to the grid corrdinate system.

The first step is to measure the grid pitch which correspond to the distance (in pixels) from one peak to the next. This is easily obtained from a pair-wise distribution function.

# pairwise distance calculation using scipy.spatial.distance_matrix

dist = distance_matrix(peaks_ref, peaks_ref)

fig, ax = subplots()
ax.hist(dist.ravel(), 100, range=(0,100))
ax.set_title("Pair-wise distribution function")
pass

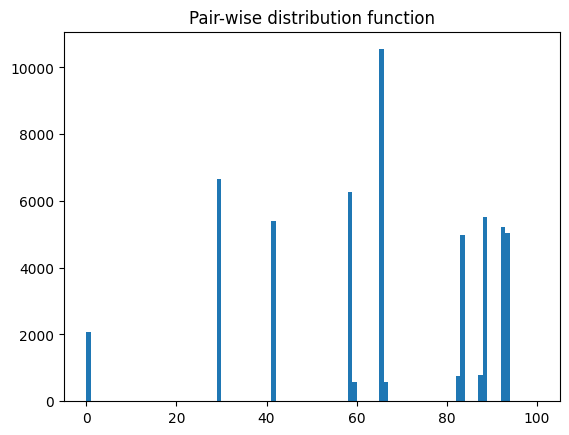
The histogram of the pair-distribution function has a first peak at 0 and the second peak between 29 and 30. Let’s start the fit with this value

Two other parameters correspond to the offset, in pixel for the grid index (X,Y) = (0,0). The easiest is to measure the smallest x and y for the first module.

#from pair-wise distribution histogram
step = 29
#work with the first module and fit the peak positions
first = yxi[yxi[:]["i"] == 1]
y_min = first[:]["y"].min()
x_min = first[:]["x"].min()
print("offset for the first peak: ", x_min, y_min)

offset for the first peak:  16.269793540239334 7.186804354190826

The grid looks very well aligned with the axes which makes this step easier but nothing garanties it is perfect, so the rotation of the grid has to be measured as well.

The default rotation will be zero and will be fitted later on.

Once the indexes X,Y determined for eack peak, one can fit the parameter to properly align the grid with the first module. Those 4 parameters are step-size, x_min, y_min and angle

#Assign each peak to an index
indexed1 = numpy.zeros(len(first), dtype=dl)

for i,v in enumerate(first):
    Y = int(round((v["y"]-y_min)/step))
    X = int(round((v["x"]-x_min)/step))
    indexed1[i]["y"] = v["y"]
    indexed1[i]["x"] = v["x"]
    indexed1[i]["i"] = v["i"]
    indexed1[i]["Y"] = Y
    indexed1[i]["X"] = X
    print("peak id: %s %20s Y:%d (Δ=%.3f) X:%s (Δ=%.3f)"%
          (i,v, Y, (v["y"]-Y*step-y_min)/step, X, (v["x"]-X*step-x_min)/step))

peak id: 0 (124.69245848059654, 16.476630687713623, 1) Y:4 (Δ=0.052) X:0 (Δ=0.007)
peak id: 1 (124.74490785598755, 45.5625721514225, 1) Y:4 (Δ=0.054) X:1 (Δ=0.010)
peak id: 2 (124.81674040853977, 75.133620262146, 1) Y:4 (Δ=0.056) X:2 (Δ=0.030)
peak id: 3 (124.75223885476589, 104.64793801307678, 1) Y:4 (Δ=0.054) X:3 (Δ=0.048)
peak id: 4 (124.84565204381943, 133.79748472571373, 1) Y:4 (Δ=0.057) X:4 (Δ=0.053)
peak id: 5 (124.85729224979877, 163.30601540207863, 1) Y:4 (Δ=0.058) X:5 (Δ=0.070)
peak id: 6 (124.8999103307724, 192.57832247018814, 1) Y:4 (Δ=0.059) X:6 (Δ=0.080)
peak id: 7 (124.96431520953774, 222.11254385113716, 1) Y:4 (Δ=0.061) X:7 (Δ=0.098)
peak id: 8 (36.49696946144104, 16.50531429052353, 1) Y:1 (Δ=0.011) X:0 (Δ=0.008)
peak id: 9 (36.54493173956871, 45.66864573955536, 1) Y:1 (Δ=0.012) X:1 (Δ=0.014)
peak id: 10 (36.57917180657387, 75.22501930594444, 1) Y:1 (Δ=0.014) X:2 (Δ=0.033)
peak id: 11 (36.485214710235596, 104.38776880502701, 1) Y:1 (Δ=0.010) X:3 (Δ=0.039)
peak id: 12 (36.59589970111847, 133.8930837586522, 1) Y:1 (Δ=0.014) X:4 (Δ=0.056)
peak id: 13 (36.56109261512756, 163.54238694906235, 1) Y:1 (Δ=0.013) X:5 (Δ=0.078)
peak id: 14 (36.629887342453, 192.6334888935089, 1) Y:1 (Δ=0.015) X:6 (Δ=0.082)
peak id: 15 (36.661303013563156, 222.22433692216873, 1) Y:1 (Δ=0.016) X:7 (Δ=0.102)
peak id: 16 (65.94893547147512, 16.45467510819435, 1) Y:2 (Δ=0.026) X:0 (Δ=0.006)
peak id: 17 (65.94483701884747, 45.613368570804596, 1) Y:2 (Δ=0.026) X:1 (Δ=0.012)
peak id: 18 (66.03506868705153, 75.15414215624332, 1) Y:2 (Δ=0.029) X:2 (Δ=0.030)
peak id: 19 (65.89957739412785, 104.3801993727684, 1) Y:2 (Δ=0.025) X:3 (Δ=0.038)
peak id: 20 (66.12287057191133, 133.89461011439562, 1) Y:2 (Δ=0.032) X:4 (Δ=0.056)
peak id: 21 (66.10124520212412, 163.3917499780655, 1) Y:2 (Δ=0.032) X:5 (Δ=0.073)
peak id: 22 (66.10113758593798, 192.66102123260498, 1) Y:2 (Δ=0.032) X:6 (Δ=0.082)
peak id: 23 (66.11095763742924, 222.20659750699997, 1) Y:2 (Δ=0.032) X:7 (Δ=0.101)
peak id: 24 (183.4998989701271, 16.392478436231613, 1) Y:6 (Δ=0.080) X:0 (Δ=0.004)
peak id: 25 (183.50560438632965, 45.46551960706711, 1) Y:6 (Δ=0.080) X:1 (Δ=0.007)
peak id: 26 (183.60742422938347, 75.08415242284536, 1) Y:6 (Δ=0.083) X:2 (Δ=0.028)
peak id: 27 (183.51583003997803, 104.62201929092407, 1) Y:6 (Δ=0.080) X:3 (Δ=0.047)
peak id: 28 (183.66220077872276, 133.73585817217827, 1) Y:6 (Δ=0.085) X:4 (Δ=0.051)
peak id: 29 (183.6555324792862, 163.3083115518093, 1) Y:6 (Δ=0.085) X:5 (Δ=0.070)
peak id: 30 (183.60811904072762, 192.46339762210846, 1) Y:6 (Δ=0.083) X:6 (Δ=0.076)
peak id: 31 (183.7554596364498, 222.06266520917416, 1) Y:6 (Δ=0.089) X:7 (Δ=0.096)
peak id: 32 (7.186804354190826, 16.41273033618927, 1) Y:0 (Δ=0.000) X:0 (Δ=0.005)
peak id: 33 (7.231230393052101, 45.745011150836945, 1) Y:0 (Δ=0.002) X:1 (Δ=0.016)
peak id: 34 (7.290591448545456, 75.19019249081612, 1) Y:0 (Δ=0.004) X:2 (Δ=0.032)
peak id: 35 (7.198769122362137, 104.56766724586487, 1) Y:0 (Δ=0.000) X:3 (Δ=0.045)
peak id: 36 (7.283639132976532, 134.01557774748653, 1) Y:0 (Δ=0.003) X:4 (Δ=0.060)
peak id: 37 (7.254908889532089, 163.38282072544098, 1) Y:0 (Δ=0.002) X:5 (Δ=0.073)
peak id: 38 (7.367172479629517, 192.76562055945396, 1) Y:0 (Δ=0.006) X:6 (Δ=0.086)
peak id: 39 (7.374693810939789, 222.16684445738792, 1) Y:0 (Δ=0.006) X:7 (Δ=0.100)
peak id: 40 (154.25518941879272, 16.269793540239334, 1) Y:5 (Δ=0.071) X:0 (Δ=0.000)
peak id: 41 (154.21079713106155, 45.57556250691414, 1) Y:5 (Δ=0.070) X:1 (Δ=0.011)
peak id: 42 (154.28871083259583, 75.04928851872683, 1) Y:5 (Δ=0.072) X:2 (Δ=0.027)
peak id: 43 (154.2160492092371, 104.43665820360184, 1) Y:5 (Δ=0.070) X:3 (Δ=0.040)
peak id: 44 (154.3742390871048, 133.86603190004826, 1) Y:5 (Δ=0.075) X:4 (Δ=0.055)
peak id: 45 (154.35255640745163, 163.24378995597363, 1) Y:5 (Δ=0.075) X:5 (Δ=0.068)
peak id: 46 (154.32582822442055, 192.64246737957, 1) Y:5 (Δ=0.074) X:6 (Δ=0.082)
peak id: 47 (154.46003967523575, 222.0459629110992, 1) Y:5 (Δ=0.078) X:7 (Δ=0.096)

The error in positionning each of the pixel is less than 0.1 pixel which is already excellent and will allow a straight forward fit.

The cost function for the first module is calculated as the sum of distances squared in pixel space. It uses 4 parameters which are step-size, x_min, y_min and angle

#Calculate the center of every single module for rotation around this center.
centers = {i: numpy.array([[numpy.where(mid == i)[1].mean()], [numpy.where(mid == i)[0].mean()]]) for i in range(1, 49)}
for k,v in centers.items():
    print(k,v.ravel())

1 [121.  97.]
2 [364.5  97. ]
3 [615.  97.]
4 [858.5  97. ]
5 [1109.   97.]
6 [1352.5   97. ]
7 [121. 309.]
8 [364.5 309. ]
9 [615. 309.]
10 [858.5 309. ]
11 [1109.  309.]
12 [1352.5  309. ]
13 [121. 521.]
14 [364.5 521. ]
15 [615. 521.]
16 [858.5 521. ]
17 [1109.  521.]
18 [1352.5  521. ]
19 [121. 733.]
20 [364.5 733. ]
21 [615. 733.]
22 [858.5 733. ]
23 [1109.  733.]
24 [1352.5  733. ]
25 [121. 945.]
26 [364.5 945. ]
27 [615. 945.]
28 [858.5 945. ]
29 [1109.  945.]
30 [1352.5  945. ]
31 [ 121. 1157.]
32 [ 364.5 1157. ]
33 [ 615. 1157.]
34 [ 858.5 1157. ]
35 [1109. 1157.]
36 [1352.5 1157. ]
37 [ 121. 1369.]
38 [ 364.5 1369. ]
39 [ 615. 1369.]
40 [ 858.5 1369. ]
41 [1109. 1369.]
42 [1352.5 1369. ]
43 [ 121. 1581.]
44 [ 364.5 1581. ]
45 [ 615. 1581.]
46 [ 858.5 1581. ]
47 [1109. 1581.]
48 [1352.5 1581. ]

# Define a rotation of a module around the center of the module ...

def rotate(angle, xy, module):
    "Perform the rotation of the xy points around the center of the given module"
    rot = [[cos(angle),-sin(angle)],
           [sin(angle), cos(angle)]]
    center = centers[module]
    return numpy.dot(rot, xy - center) + center

guess1 = [step, y_min, x_min, 0]

def cost1(param):
    """contains: step, y_min, x_min, angle for the first module
    returns the sum of distance squared in pixel space
    """
    step = param[0]
    y_min = param[1]
    x_min = param[2]
    angle = param[3]
    XY = numpy.vstack((indexed1["X"], indexed1["Y"]))
#     rot = [[cos(angle),-sin(angle)],
#            [sin(angle), cos(angle)]]
    xy_min = [[x_min], [y_min]]
    xy_guess = rotate(angle, step * XY + xy_min, module=1)
    delta = xy_guess - numpy.vstack((indexed1["x"], indexed1["y"]))
    return (delta*delta).sum()

print("Before optimization", guess1, "cost=", cost1(guess1))
res1 = minimize(cost1, guess1, method = "slsqp")
print(res1)
print("After optimization", res1.x, "cost=", cost1(res1.x))
print("Average displacement (pixels): ",sqrt(cost1(res1.x)/len(indexed1)))

Before optimization [29, np.float64(7.186804354190826), np.float64(16.269793540239334), 0] cost= 250.36710826038228
 message: Optimization terminated successfully
 success: True
  status: 0
     fun: 0.6337541947714561
       x: [ 2.940e+01  7.242e+00  1.631e+01  8.769e-04]
     nit: 8
     jac: [-1.664e-05  4.396e-07  2.012e-07  8.898e-04]
    nfev: 54
    njev: 8
After optimization [2.93980816e+01 7.24220065e+00 1.63128834e+01 8.76927130e-04] cost= 0.6337541947714561
Average displacement (pixels):  0.11490523221799781

At this step, the grid is perfectly aligned with the first module. This module is used as the reference one and all other are aligned along it, using this first fit:

#retrieve the result of the first module fit:
step, y_min, x_min, angle = res1.x
indexed = numpy.zeros(yxi.shape, dtype=dl)

# rot =  [[cos(angle),-sin(angle)],
#         [sin(angle), cos(angle)]]
# irot =  [[cos(angle), sin(angle)],
#          [-sin(angle), cos(angle)]]

print("cost1: ",cost1([step, y_min, x_min, angle]), "for:", step, y_min, x_min, angle)

xy_min = numpy.array([[x_min], [y_min]])
xy = numpy.vstack((yxi["x"], yxi["y"]))
indexed["y"] = yxi["y"]
indexed["x"] = yxi["x"]
indexed["i"] = yxi["i"]
XY_app = (rotate(-angle, xy, 1)-xy_min) / step
XY_int = numpy.round((XY_app)).astype("int")
indexed["X"] = XY_int[0]
indexed["Y"] = XY_int[1]
xy_guess = rotate(angle, step * XY_int + xy_min, 1)

thres = 1.2
delta = abs(xy_guess - xy)
print((delta>thres).sum(), "suspicious peaks:")
suspicious = indexed[numpy.where(abs(delta>thres))[1]]
print(suspicious)

cost1:  0.6337541947714561 for: 29.398081602009334 7.242200648233459 16.3128833618955 0.0008769271297656559
6 suspicious peaks:
[(1624.68617365, 807.47743243, 46, 55, 27)
 (1654.4202804 , 954.44135761, 46, 56, 32)
 (1595.5792897 , 954.49445057, 46, 54, 32)
 (1448.30209509, 748.8784325 , 40, 49, 25)
 (1448.66381988, 895.86545633, 40, 49, 30)
 (1448.84506877, 954.56920397, 40, 49, 32)]

fig,ax = subplots()
ax.imshow(img.clip(0,1000))
ax.plot(indexed["x"], indexed["y"],".g")
ax.plot(suspicious["x"], suspicious["y"],".r")
pass

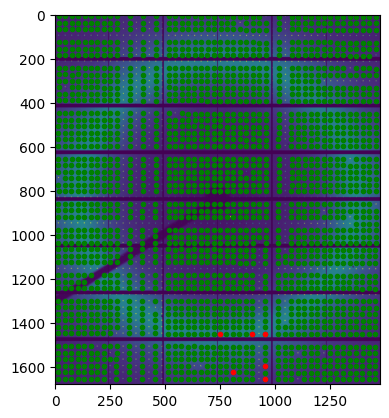
Only 6 peaks have an initial displacement of more than 1.2 pixel, all located in modules 40 and 46. The visual inspection confirms their localization is valid.

There are 48 (half-)modules which have each of them 2 translations and one rotation. In addition to the step size, this represents 145 degrees of freedom for the fit. The first module is used to align the grid, all other modules are then aligned along this grid.

def submodule_cost(param, module=1):
    """contains: step, y_min_1, x_min_1, angle_1, y_min_2, x_min_2, angle_2, ...
    returns the sum of distance squared in pixel space
    """

    step = param[0]
    y_min1 = param[1]
    x_min1 = param[2]
    angle1 = param[3]

    mask = indexed["i"] == module
    substack = indexed[mask]

    XY = numpy.vstack((substack["X"], substack["Y"]))
#     rot1 = [[cos(angle1), -sin(angle1)],
#             [sin(angle1), cos(angle1)]]
    xy_min1 = numpy.array([[x_min1], [y_min1]])
    xy_guess1 = rotate(angle1, step * XY + xy_min1, module=1)
    #This is guessed spot position for module #1
    if module == 1:
        "Not much to do for module 1"
        delta = xy_guess1 - numpy.vstack((substack["x"], substack["y"]))
    else:
        "perform the correction for given module"
        y_min = param[(module-1)*3+1]
        x_min = param[(module-1)*3+2]
        angle = param[(module-1)*3+3]

#         rot = numpy.array([[cos(angle),-sin(angle)],
#                            [sin(angle), cos(angle)]])
        xy_min = numpy.array([[x_min], [y_min]])
        xy_guess = rotate(angle, xy_guess1+xy_min, module)
        delta = xy_guess - numpy.vstack((substack["x"], substack["y"]))

    return (delta*delta).sum()

guess145 = numpy.zeros(48*3+1)
guess145[:4] = res1.x
for i in range(1, 49):
    print("Cost for module #",i, submodule_cost(guess145, i))

Cost for module # 1 0.6337541947714561
Cost for module # 2 1.8140316108131798
Cost for module # 3 1.8508565514988509
Cost for module # 4 4.9103267577570255
Cost for module # 5 1.774874937412774
Cost for module # 6 7.482509531429409
Cost for module # 7 14.440094686407006
Cost for module # 8 5.219967185609465
Cost for module # 9 23.407234105446342
Cost for module # 10 5.68998070432852
Cost for module # 11 4.1255770771863345
Cost for module # 12 8.410827679528012
Cost for module # 13 29.85982022785213
Cost for module # 14 12.628452333847438
Cost for module # 15 3.1377088713448913
Cost for module # 16 5.277309670415619
Cost for module # 17 8.497326191628567
Cost for module # 18 4.6531481100073915
Cost for module # 19 6.007095311701259
Cost for module # 20 4.980267142822849
Cost for module # 21 5.136966460516821
Cost for module # 22 5.048720859903036
Cost for module # 23 1.4373122720991895
Cost for module # 24 6.046291144378303
Cost for module # 25 38.25446688404895
Cost for module # 26 19.50979678797815
Cost for module # 27 2.4297101474978002
Cost for module # 28 5.488602401759433
Cost for module # 29 10.764107827570434
Cost for module # 30 14.042160565198424
Cost for module # 31 22.940123155012884
Cost for module # 32 18.493732165939573
Cost for module # 33 12.941765922197542
Cost for module # 34 15.371708188594887
Cost for module # 35 39.66701930023118
Cost for module # 36 37.28279372517758
Cost for module # 37 63.700698814437914
Cost for module # 38 23.54951672171008
Cost for module # 39 34.004282341400625
Cost for module # 40 43.803709729886506
Cost for module # 41 15.505216286622526
Cost for module # 42 8.048820008829708
Cost for module # 43 22.73536148509508
Cost for module # 44 10.7960222922627
Cost for module # 45 41.019680015289275
Cost for module # 46 46.25894226140755
Cost for module # 47 24.54658044719688
Cost for module # 48 34.76960701421626

On retrieves that the modules 40 and 46 have large errors. Module 37 as well.

The total cost funtion is hence the sum of all cost function for all modules:

def total_cost(param):
    """contains: step, y_min_1, x_min_1, angle_1, ...
    returns the sum of distance squared in pixel space
    """
    return sum(submodule_cost(param, module=i) for i in range(1,49))
total_cost(guess145)

np.float64(778.3948781082676)

%%time
print("Before optimization", guess145[:10], "cost=", total_cost(guess145))
res_all = minimize(total_cost, guess145, method = "slsqp")
print(res_all)
print("After optimization", res_all.x[:10], "cost=", total_cost(res_all.x))

Before optimization [2.93980816e+01 7.24220065e+00 1.63128834e+01 8.76927130e-04
 0.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+00
 0.00000000e+00 0.00000000e+00] cost= 778.3948781082676
 message: Optimization terminated successfully
 success: True
  status: 0
     fun: 27.184565783818048
       x: [ 2.941e+01  7.212e+00 ... -9.241e-01  1.891e-03]
     nit: 89
     jac: [-1.687e+00 -2.310e-02 ... -8.608e-03  4.117e-03]
    nfev: 13373
    njev: 89
After optimization [ 2.94082827e+01  7.21153863e+00  1.62772294e+01  8.29112877e-04
 -1.49128333e-01 -1.98983536e-01  3.22806910e-04  1.25931838e-01
 -2.38725530e-01  9.70931854e-04] cost= 27.184565783818048
CPU times: user 35.1 s, sys: 93.8 ms, total: 35.2 s
Wall time: 35.1 s

for i in range(1,49):
    print("Module id: %d cost: %.3f Δx: %.3f, Δy: %.3f rot: %.3f°"%
          (i, submodule_cost(res_all.x, i), res_all.x[-2+i*3], res_all.x[-1+i*3], numpy.rad2deg(res_all.x[i*3])))

Module id: 1 cost: 0.684 Δx: 7.212, Δy: 16.277 rot: 0.048°
Module id: 2 cost: 0.473 Δx: -0.149, Δy: -0.199 rot: 0.018°
Module id: 3 cost: 0.650 Δx: 0.126, Δy: -0.239 rot: 0.056°
Module id: 4 cost: 0.613 Δx: 0.290, Δy: -0.226 rot: 0.114°
Module id: 5 cost: 0.566 Δx: -0.075, Δy: -0.465 rot: 0.021°
Module id: 6 cost: 0.666 Δx: 0.316, Δy: -0.641 rot: 0.122°
Module id: 7 cost: 0.696 Δx: -0.599, Δy: 0.075 rot: 0.080°
Module id: 8 cost: 0.341 Δx: -0.429, Δy: -0.134 rot: 0.065°
Module id: 9 cost: 0.566 Δx: -0.699, Δy: -0.414 rot: 0.054°
Module id: 10 cost: 0.661 Δx: -0.210, Δy: -0.454 rot: 0.123°
Module id: 11 cost: 0.616 Δx: 0.237, Δy: -0.266 rot: 0.030°
Module id: 12 cost: 0.495 Δx: 0.344, Δy: -0.172 rot: 0.040°
Module id: 13 cost: 0.763 Δx: -0.685, Δy: -0.571 rot: 0.068°
Module id: 14 cost: 0.353 Δx: -0.510, Δy: -0.583 rot: 0.078°
Module id: 15 cost: 0.645 Δx: -0.289, Δy: -0.334 rot: 0.058°
Module id: 16 cost: 0.492 Δx: -0.018, Δy: -0.555 rot: 0.076°
Module id: 17 cost: 0.440 Δx: -0.295, Δy: -0.764 rot: 0.028°
Module id: 18 cost: 0.779 Δx: -0.028, Δy: -0.684 rot: 0.091°
Module id: 19 cost: 0.748 Δx: -0.482, Δy: -0.229 rot: 0.043°
Module id: 20 cost: 0.423 Δx: -0.218, Δy: -0.494 rot: 0.044°
Module id: 21 cost: 0.520 Δx: -0.420, Δy: -0.413 rot: -0.014°
Module id: 22 cost: 0.676 Δx: -0.237, Δy: -0.555 rot: 0.096°
Module id: 23 cost: 0.503 Δx: -0.168, Δy: -0.292 rot: 0.074°
Module id: 24 cost: 0.822 Δx: 0.128, Δy: -0.414 rot: 0.098°
Module id: 25 cost: 0.575 Δx: -0.741, Δy: -0.797 rot: 0.057°
Module id: 26 cost: 0.320 Δx: -0.397, Δy: -0.879 rot: 0.103°
Module id: 27 cost: 0.642 Δx: -0.085, Δy: -0.234 rot: -0.027°
Module id: 28 cost: 0.599 Δx: 0.058, Δy: -0.265 rot: 0.037°
Module id: 29 cost: 0.498 Δx: -0.089, Δy: -0.852 rot: 0.035°
Module id: 30 cost: 0.830 Δx: 0.177, Δy: -0.644 rot: 0.136°
Module id: 31 cost: 0.687 Δx: -0.557, Δy: -0.712 rot: -0.040°
Module id: 32 cost: 0.422 Δx: -0.675, Δy: -0.813 rot: 0.085°
Module id: 33 cost: 0.616 Δx: -0.163, Δy: -0.692 rot: -0.034°
Module id: 34 cost: 0.393 Δx: -0.030, Δy: -0.815 rot: 0.092°
Module id: 35 cost: 0.447 Δx: -0.194, Δy: -1.300 rot: 0.039°
Module id: 36 cost: 0.587 Δx: -0.039, Δy: -1.308 rot: 0.035°
Module id: 37 cost: 0.603 Δx: -1.027, Δy: -1.048 rot: 0.001°
Module id: 38 cost: 0.295 Δx: -0.931, Δy: -0.901 rot: 0.001°
Module id: 39 cost: 0.558 Δx: -0.576, Δy: -1.054 rot: 0.009°
Module id: 40 cost: 0.498 Δx: -0.251, Δy: -1.286 rot: 0.142°
Module id: 41 cost: 0.468 Δx: -0.164, Δy: -0.940 rot: 0.022°
Module id: 42 cost: 0.569 Δx: -0.202, Δy: -0.830 rot: 0.038°
Module id: 43 cost: 0.633 Δx: -0.833, Δy: -0.669 rot: 0.059°
Module id: 44 cost: 0.413 Δx: -0.627, Δy: -0.771 rot: 0.034°
Module id: 45 cost: 0.671 Δx: -0.539, Δy: -1.178 rot: -0.018°
Module id: 46 cost: 0.542 Δx: -0.372, Δy: -1.357 rot: 0.076°
Module id: 47 cost: 0.537 Δx: -0.078, Δy: -1.021 rot: 0.069°
Module id: 48 cost: 0.593 Δx: 0.255, Δy: -0.924 rot: 0.108°

Analysis: Modules 40, 46 and 48 show large displacement but the fitting precedure allowed to reduce the residual cost to the same value as other modules.

Reconstruction of the pixel position

The pixel position can be obtained from the standard Pilatus detector. Each module is then displaced according to the fitted values, except the first one which is left where it is.

def correct(x, y, dx, dy, angle, module):
    "apply the correction dx, dy and angle to those pixels ..."
    trans = numpy.array([[dx],
                         [dy]])
    xy_guess = numpy.vstack((x.ravel(),
                             y.ravel()))
    xy_cor = rotate(-angle, xy_guess, module) - trans
    xy_cor.shape = ((2,)+x.shape)
    return xy_cor[0], xy_cor[1]

pixel_coord = pyFAI.detector_factory("Pilatus2MCdTe").get_pixel_corners()
pixel_coord_raw = pixel_coord.copy()
for i in range(2, 49):
    # Extract the pixel corners for one module
    module_idx = numpy.where(mid == i)
    one_module = pixel_coord_raw[module_idx]
    #retrieve the fitted values
    dy, dx, angle = res_all.x[-2+i*3:1+3*i]

    y = one_module[..., 1]/pilatus.pixel1
    x = one_module[..., 2]/pilatus.pixel2

    #apply the correction the other way around
    x_cor, y_cor = correct(x, y, dx, dy, angle, i)
    one_module[...,1] = y_cor * pilatus.pixel1 #y
    one_module[...,2] = x_cor * pilatus.pixel2 #x
    #Update the array
    pixel_coord_raw[module_idx] = one_module

Update the detector and save it in HDF5

pilatus.set_pixel_corners(pixel_coord_raw)
pilatus.mask = all_masks
pilatus.save("Pilatus_ID15_raw.h5")

displ = numpy.sqrt(((pixel_coord - pixel_coord_raw)**2).sum(axis=-1))
displ /= pilatus.pixel1 #convert in pixel units
fig, ax = subplots()
ax.hist(displ.ravel(), 100)
ax.set_title("Displacement of pixels versus the reference representation")
ax.set_xlabel("Error in pixel size (172µm)")
pass

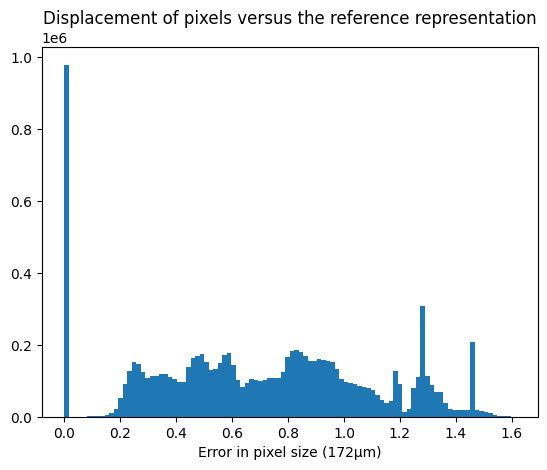
misaligned = numpy.vstack((pixel_coord_raw[..., 2].ravel(), #x
                           pixel_coord_raw[..., 1].ravel())) #y

reference = numpy.vstack((pixel_coord[..., 2].ravel(), #x
                          pixel_coord[..., 1].ravel())) #y

#Kabsch alignment of the whole detector ...

def kabsch(P, R):
    "Align P on R"
    centroid_P = P.mean(axis=0)
    centroid_R = R.mean(axis=0)
    centered_P = P - centroid_P
    centered_R = R - centroid_R
    C = numpy.dot(centered_P.T, centered_R)
    V, S, W = numpy.linalg.svd(C)
    d = (numpy.linalg.det(V) * numpy.linalg.det(W)) < 0.0
    if d:
        S[-1] = -S[-1]
        V[:, -1] = -V[:, -1]
    # Create Rotation matrix U
    U = numpy.dot(V, W)
    P = numpy.dot(centered_P, U)
    return P + centroid_R

%time aligned = kabsch(misaligned.T, reference.T).T

CPU times: user 2.49 s, sys: 54.5 ms, total: 2.55 s
Wall time: 275 ms

displ = numpy.sqrt(((aligned-reference)**2).sum(axis=0))
displ /= pilatus.pixel1 #convert in pixel units
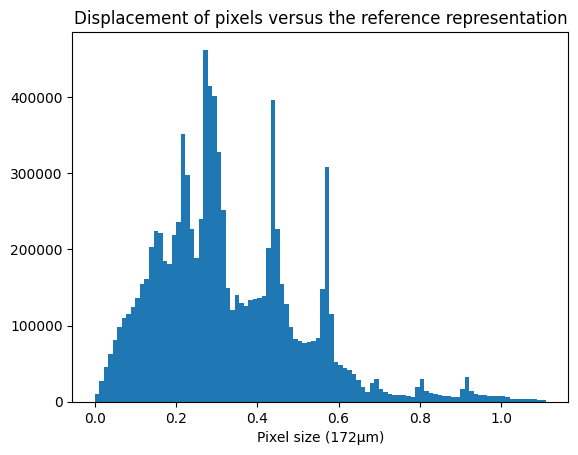
fig, ax = subplots()
ax.hist(displ.ravel(), 100)
ax.set_title("Displacement of pixels versus the reference representation")
ax.set_xlabel("Pixel size (172µm)")
pass

pixel_coord_aligned = pixel_coord.copy()
pixel_coord_aligned[...,1] = aligned[1,:].reshape(pixel_coord.shape[:-1])
pixel_coord_aligned[...,2] = aligned[0,:].reshape(pixel_coord.shape[:-1])

pilatus.set_pixel_corners(pixel_coord_aligned)
pilatus.mask = all_masks
pilatus.save("Pilatus_ID15_Kabsch.h5")

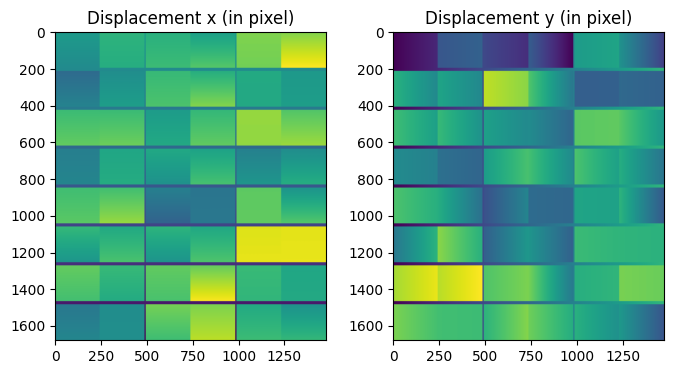
fig, ax = subplots(1, 2, figsize=(8, 4))
ax[0].imshow((pixel_coord_aligned[...,2].mean(axis=-1) - pixel_coord[...,2].mean(axis=-1))/pilatus.pixel2)
ax[0].set_title("Displacement x (in pixel)")
ax[1].imshow((pixel_coord_aligned[...,1].mean(axis=-1) - pixel_coord[...,1].mean(axis=-1))/pilatus.pixel1)
ax[1].set_title("Displacement y (in pixel)")
pass

Validation of the result

To validate the improvement obtained, one can perform the experiment calibration and the 2D integration of a reference compound, the 2D integration with either the reference from Dectris or this freshly refined detector.

# The geometry has been obtained from pyFAI
geo = { "dist":  0.8001094657585498,
        "poni1": 0.14397714477803805,
        "poni2": 0.12758748978422835,
        "rot1":  0.0011165686147339689,
        "rot2":  0.0002214091645638961,
        "rot3":  0,
        "detector": "Pilatus2MCdTe"}
ai_unc = AzimuthalIntegrator(**geo)
geo["detector"] = "Pilatus_ID15_Kabsch.h5"
ai_cor = AzimuthalIntegrator(**geo)
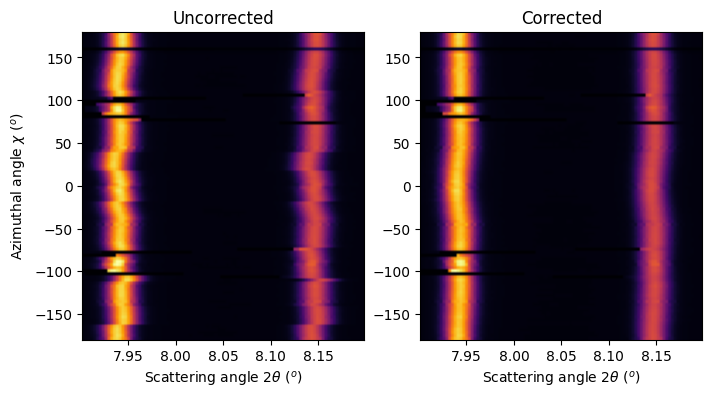
fig, ax = subplots(1, 2, figsize=(8,4))
method = ("pseudo", "histogram", "cython")
res_unc = ai_unc.integrate2d_ng(rings, 100, 100, radial_range=(7.9, 8.2), unit="2th_deg", method=method, mask=all_masks)
res_cor = ai_cor.integrate2d_ng(rings, 100, 100, radial_range=(7.9, 8.2), unit="2th_deg", method=method, mask=all_masks)
opts = {"origin":"lower",
        "extent": [res_unc.radial.min(), res_unc.radial.max(), -180, 180],
        "aspect":"auto",
        "cmap":"inferno"}
ax[0].imshow(res_unc[0], **opts)
ax[1].imshow(res_cor[0], **opts)
ax[0].set_xlabel(r"Scattering angle 2$\theta$ ($^{o}$)")
ax[1].set_xlabel(r"Scattering angle 2$\theta$ ($^{o}$)")
ax[0].set_ylabel(r"Azimuthal angle $\chi$ ($^{o}$)")
ax[0].set_title("Uncorrected")
ax[1].set_title("Corrected")
pass

Conclusion

This tutorial presents the way to calibrate a module based detector using the Pilatus2M CdTe from ESRF-ID15. The HDF5 file generated is directly useable by any parts of pyFAI, the reader is invited in calibrating the rings images with the default definition and with this optimized definition and check the residual error is almost divided by a factor two.

To come back on the precision of the localization of the pixel: not all the pixel are within the specifications provided by Dectris which claims the misaliment of the modules is within one pixel.

print(f"Total execution time: {time.perf_counter()-start_time:.3f}s")

Total execution time: 98.215s